$ΔL$ Normalization: Rethink Loss Aggregation in RLVR
-
ArXiv URL: http://arxiv.org/abs/2509.07558v1
-
作者: Xufang Luo; Yike Zhang; Lili Qiu; Yuqing Yang; Zhiyuan He
-
发布机构: Microsoft Research; Tsinghua University
TL;DR
本文提出了一种名为 $ΔL$ 的新型损失聚合方法，通过构建一个无偏且方差最小的策略梯度估计器，有效解决了在带可验证奖励的强化学习（RLVR）中因响应长度变化巨大导致的高梯度方差和训练不稳定问题。
关键定义
本文的核心论述建立在对现有方法的统一分析和统计学优化之上，关键定义如下：
- 带可验证奖励的强化学习 (Reinforcement Learning with Verifiable Rewards, RLVR)：一种应用于提升大语言模型（LLMs）推理能力的强化学习范式。其特点是奖励函数基于规则进行判断（例如，数学题的答案是否正确），而非学习出来的奖励模型。
- 无范数化样本级梯度 (Unnormalized Sample-Level Gradient, $\mathbf{g}_{i}$)：为统一分析各类方法，本文定义了单个样本（响应）在进行任何长度归一化之前的梯度，其数学形式为 $\mathbf{g}_{i} = \nabla_{\theta}\sum_{t=1}^{L_{i}}(\dots)$。理论上，其期望 $\mathbb{E}[\mathbf{g}_{i}]$ 近似于真实的策略梯度。
- 有偏/无偏估计 (Biased/Unbiased Estimation)：指梯度估计器的期望是否与真实策略梯度成一个固定比例。有偏估计器（如 GRPO、DAPO）的期望会受到响应长度 $L_i$ 的影响，导致训练后期梯度范数减小，收敛变慢。无偏估计器（如 Dr. GRPO、本文的 $ΔL$）则避免了此问题。
- 变异系数 (Coefficient of Variation, CV)：定义为 $\mathrm{CV}(\mathbf{g}) = \frac{\sqrt{\mathrm{Var}(\mathbf{g})}}{ \mid \mid \mathbb{E}(\mathbf{g}) \mid \mid }$，用于衡量梯度的相对波动。它标准化了不同期望范数下的方差，是比较不同估计器稳定性的关键指标。CV 越小，训练越稳定。
相关工作
当前，带可验证奖励的强化学习（RLVR）在提升大语言模型推理能力方面取得了显著进展。然而，RLVR 训练面临一个独特的挑战：模型生成的响应轨迹在长度上差异巨大，从几十到几千个 token 不等，且长度通常随训练进行而增长。这种长度的剧烈变化会导致梯度方差过高，进而造成训练不稳定甚至模型性能崩溃。
为了解决这个问题，现有工作提出了不同的损失聚合（即梯度聚合）策略：
- GRPO：对每个样本的损失（梯度）除以其各自的长度 $L_i$ 进行归一化。
- DAPO：将一个批次内所有样本的梯度相加后，再除以批次内所有响应的总长度 $\sum L_i$。
- Dr. GRPO：不使用与长度相关的因子，而是用一个固定的常数 $M$ 来归一化梯度。
尽管这些方法在经验上取得了一定的效果，但缺乏系统的理论分析。本文通过分析发现，GRPO 和 DAPO 引入了与长度相关的偏见（Bias），导致训练后期收敛速度减慢；同时，DAPO 和 Dr. GRPO 会产生较高的梯度方差（具体为高变异系数 CV），导致训练过程不稳定。
因此，本文旨在解决的核心问题是：如何设计一种损失聚合方法，使其既能提供对真实策略梯度的无偏估计，又能从理论上最小化梯度方差，从而实现稳定高效的 RLVR 训练？
本文方法
理论分析与问题重构
本文首先从一个统一的视角重新审视了现有的损失聚合方法。所有方法都可以看作是对一系列无范数化样本级梯度 ${\mathbf{g}_i}_{i=1}^G$ 的线性组合。
核心观察：梯度方差与响应长度成正比
通过理论推导和经验验证，本文确认了一个关键的统计特性：单个样本的梯度方差与其响应长度成正比，即 $\mathrm{Var}(\mathbf{g}_i) \approx V \cdot L_i$，其中 $V$ 是一个常数。这意味着更长的响应会自然地引入更大的梯度噪声，这是导致训练不稳定的根源。
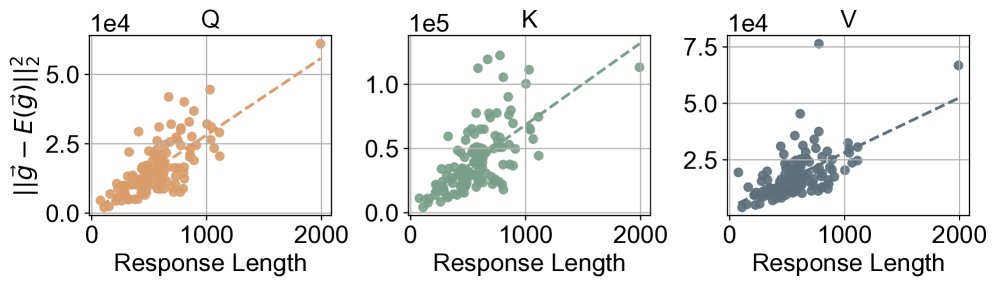上图显示，样本梯度与其期望梯度的偏差平方（即方差的体现）随着响应长度的增加而线性增长。
现有方法的偏见-方差剖析
基于上述观察，本文对现有方法进行了偏见-方差分析，总结如下表：
| 方法 | $E(\mathbf{g})$ (期望) | $\mathrm{Var}(\mathbf{g})$ (方差) | $\mathrm{CV}(\mathbf{g})$ (变异系数) |
|---|---|---|---|
| GRPO | $\left(\tfrac{1}{G}\sum_{i=1}^{G}\tfrac{1}{L_{i}}\right)\nabla_{\theta}J(\theta)$ | $\tfrac{V}{G^{2}}\sum_{i=1}^{G}\tfrac{1}{L_{i}}$ | $\left({\sqrt{\sum_{i=1}^{G}\tfrac{1}{L_{i}}}}\right)^{-1}\cdot\tfrac{\sqrt{V}}{\ \mid \nabla_{\theta}J(\theta)\ \mid }$ $\downarrow$ 低 |
| DAPO | $\left(\tfrac{G}{\sum_{i=1}^{G}L_{i}}\right)\nabla_{\theta}J(\theta)$ | $\tfrac{V}{\sum_{i=1}^{G}L_{i}}$ | $\tfrac{\sqrt{\sum_{i=1}^{G}L_{i}}}{G}\cdot\tfrac{\sqrt{V}}{\ \mid \nabla_{\theta}J(\theta)\ \mid }$ $\uparrow$ 高 |
| Dr. GRPO | $\tfrac{1}{M}\nabla_{\theta}J(\theta)$ | $\tfrac{V\sum_{i=1}^{G}L_{i}}{G^{2}M^{2}}$ | $\tfrac{\sqrt{\sum_{i=1}^{G}L_{i}}}{G}\cdot\tfrac{\sqrt{V}}{\ \mid \nabla_{\theta}J(\theta)\ \mid }$ $\uparrow$ 高 |
| Ours ($ΔL$) | $\tfrac{1}{M}\nabla_{\theta}J(\theta)$ | $\tfrac{V}{M^{2}\sum_{i=1}^{G}\tfrac{1}{L_{i}}}$ | $\left({\sqrt{\sum_{i=1}^{G}\tfrac{1}{L_{i}}}}\right)^{-1}\cdot\tfrac{\sqrt{V}}{\ \mid \nabla_{\theta}J(\theta)\ \mid }$ $\downarrow$ 低 |
- 和 分别表示有偏和无偏估计。
此分析揭示了：
- GRPO 和 DAPO 是有偏的：其梯度期望受变化的 $L_i$ 影响，随着训练中响应变长，梯度范数会缩小，拖慢收敛。
- DAPO 和 Dr. GRPO 具有高变异系数（CV）：这意味着它们的梯度更新信噪比较低，更容易产生不稳定的优化。
$ΔL$：无偏最小方差估计器
为了同时解决偏见和高方差问题，本文将损失聚合问题重构成一个经典的统计优化问题：寻找最佳线性无偏估计器（Best Linear Unbiased Estimator）。
具体地，任务是寻找一组系数 ${x_i}$，构造聚合梯度 $\hat{\mathbf{g}} = \sum_{i=1}^{G} x_i \mathbf{g}_i$，使其满足：
- 无偏性: $\mathbb{E}[\hat{\mathbf{g}}]$ 与真实梯度 $\nabla_{\theta}J(\theta)$ 成一个固定比例，即 $\sum_{i=1}^{G} x_i = \text{const}$。
- 最小方差: $\mathrm{Var}[\hat{\mathbf{g}}]$ 达到最小。
利用拉格朗日乘子法求解该约束优化问题，得到最优权重 $x_i^{\star}$ 应与 $\frac{1}{\mathrm{Var}(\mathbf{g}_i)}$ 成正比。考虑到 $\mathrm{Var}(\mathbf{g}_i) \propto L_i$，则最优权重 $x_i^{\star} \propto \frac{1}{L_i}$。
创新点
本文提出的 $ΔL$ 方法正是基于此原理，并引入超参数 $\alpha$ 来提供灵活性。其聚合权重的计算方式为：
\[x_{i}=\frac{1}{M}\frac{L_{i}^{-\alpha}}{\sum_{j=1}^{G}L_{j}^{-\alpha}}, \quad i=1,\dots,G\]其中 $M$ 是一个固定缩放常数。
优点
- 无偏性：对于任意 $\alpha$，权重之和 $\sum x_i = \frac{1}{M}$ 是一个常数，确保了梯度估计是无偏的，这与标准强化学习理论保持一致，避免了后期收敛减速的问题。
- 最小化方差：当设置 $\alpha=1$ 时，$ΔL$ 提供了理论上可能的最小方差，从而最大化训练稳定性。其变异系数（CV）与 GRPO 相同，且显著低于 DAPO 和 Dr. GRPO。
- 统一框架和灵活性：
- $\alpha=1$ 对应最小方差，牺牲了长响应的贡献。
- $\alpha=0$ 时，$ΔL$ 退化为 Dr. GRPO 的聚合方式。
- $0 < \alpha < 1$ 提供了一个权衡，允许信息量更丰富的长响应发挥更大作用，代价是方差略微增加。
- 实现简单：该方法仅需修改几行代码即可实现，易于集成。
实验结论
本文在 CountDown 和 Math 两个任务上，使用 Qwen2.5-3B 和 Qwen2.5-7B 模型进行了广泛实验。
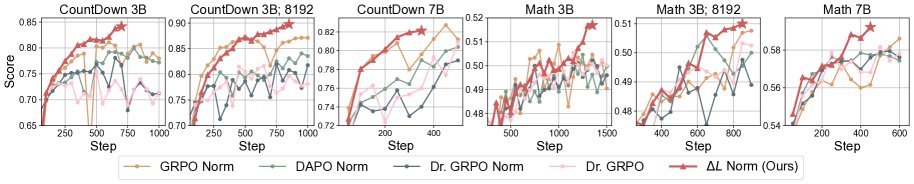上图展示了在不同任务、模型和最大长度设置下，$ΔL$ 与基线方法的训练动态对比。$ΔL$ 普遍实现了更稳定的训练和更高的收敛精度。
关键实验结果
- 普遍优越性：在几乎所有实验设置中，$ΔL$ 都取得了比 GRPO、DAPO 和 Dr. GRPO 等基线方法更好或相当的性能。训练过程更稳定，收敛后的最终准确率也更高。
- 训练稳定性：$ΔL$ 展现出高度的性能单调性（即性能随训练步数稳定提升），其 “monotonicity score” 显著高于其他方法。同时，它有效避免了高 CV 方法（如 DAPO）中常见的熵爆炸和性能骤降现象。
- 对长响应的处理：与 DAPO 中复杂的“超长过滤”或“软惩罚”机制相比，$ΔL$ 提供了一个更简单、更统一且效果更好的方案来处理长响应带来的方差问题。实验证明，将 DAPO 的其他组件（如动态采样）与 $ΔL$ 结合，性能优于完整的 DAPO 方法。
不同场景下的表现
- 在 CountDown 任务中，长响应通常是冗余的，最小化方差（$\alpha=1$）的 $ΔL$ 表现出色。
- 在 Math 任务中，长响应可能包含更复杂的推理链，更有价值。实验发现，使用 $\alpha=0.75$ 的 $ΔL$（允许长响应有更大贡献）比 $\alpha=1$ 效果更好，但两者均优于基线。
- 所有测试的 $\alpha$ 值（0.5, 0.75, 1.0）在多数情况下都优于所有基线方法，证明了 $ΔL$ 的鲁棒性。$\alpha=1$ 是一个安全且效果良好的默认选择。
最终结论
$ΔL$ 方法被证明是一种非常有效的损失聚合策略。它通过在理论上保证无偏性和最小化方差，成功解决了 RLVR 训练中的核心痛点，带来了更稳定、高效的训练过程和更强的模型性能。