A General Theoretical Paradigm to Understand Learning from Human Preferences

• ArXiv URL: http://arxiv.org/abs/2310.12036v2

• 作者: Michal Valko; Mark Rowland; Bilal Piot; Rémi Munos; M. G. Azar; Daniele Calandriello; Daniel Guo

• 发布机构: Google DeepMind

---

TL;DR

本文提出了一个名为 Ψ-偏好优化 (ΨPO) 的通用理论框架，该框架统一了现有的从人类偏好中学习的方法（如 RLHF 和 DPO），并在此基础上提出了一种名为 IPO 的新方法，它通过直接优化成对偏好而非依赖 Bradley-Terry 模型，有效解决了 DPO 在面对确定性或稀疏偏好数据时容易出现的过拟合问题。

关键定义

• Ψ-偏好优化 (Ψ-preference optimisation, ΨPO)：本文提出的一个通用目标函数，用于从人类偏好中学习策略。其核心思想是在最大化一个关于“偏好概率”的非递减函数 \(Ψ(p*)\) 的期望与最小化策略 \(π\) 相对于参考策略 \(π_ref\) 的 KL 散度之间进行权衡。目标函数如下：

  \[\max_{\pi} \underset{\begin{subarray}{c} x \sim \rho \\ y \sim \pi \left( \cdot \mid x \right) \\ y' \sim \mu \left( \cdot \mid x \right) \end{subarray}}{\mathbb{E}} \left[ \Psi(p^*(y \succ y' \mid x)) \right] - \tau D_{\text{KL}}(\pi \mid \mid \pi_{\text{ref}})\]

• 恒等偏好优化 (Identity-PO, IPO)：ΨPO 的一个特例，其中函数 \(Ψ\) 被设置为恒等映射 (\(Ψ(p) = p\))。该方法直接优化策略的“总偏好”，旨在绕开 Bradley-Terry 模型假设，从而增强算法的鲁棒性，避免过拟合。其目标函数为：

  \[\max_{\pi} p_{\rho}^*(\pi \succ \mu) - \tau D_{\text{KL}}(\pi \parallel \pi_{\text{ref}})\]

相关工作

当前，从人类偏好中学习（Learning from Human Preferences）的主流方法是基于人类反馈的强化学习 (Reinforcement Learning from Human Feedback, RLHF) 和直接偏好优化 (Direct Preference Optimisation, DPO)。

• 研究现状：RLHF 通过两阶段过程（学习奖励模型 + RL 策略优化）来对齐大型语言模型，取得了巨大成功。DPO 作为一种更简洁的替代方案，通过直接从偏好数据中优化策略，避免了显式的奖励建模，在一些任务上表现出与 RLHF 相当的性能。

• 存在问题：尽管这些方法在实践中很有效，但其理论基础尚不明确。RLHF 依赖两个关键近似：（1）假设成对偏好可以通过 Bradley-Terry (BT) 模型转化为点态奖励 (pointwise rewards)；（2）假设学习到的奖励模型可以泛化到策略采样的新数据上。DPO 绕过了第二个近似，但仍然严重依赖第一个 BT 模型假设。当偏好数据是确定性的（即一个选项总是优于另一个）或接近确定性时，这种依赖会导致 KL 正则化项失效，从而引发严重的过拟合问题。

• 本文目标：本文旨在弥合理论与实践之间的差距，通过引入一个更通用的理论框架 (ΨPO) 来深入理解 RLHF 和 DPO 的行为机制，识别它们的潜在缺陷，并提出一个更稳健、不易过拟合的新方法 (IPO)。

本文方法

通用目标：ΨPO

本文提出了一个名为 Ψ-偏好优化 (ΨPO) 的通用目标函数，它将从人类偏好中学习的问题形式化为最大化偏好概率的某个函数 \(Ψ(p*)\) 与 KL 正则化项的权衡。

通过选择不同的 \(Ψ\) 函数，这个通用目标可以涵盖现有的方法。具体而言，当选择 \(Ψ(q) = log(q/(1-q))\) 并且假设真实的偏好 \(p*\) 遵循 Bradley-Terry (BT) 模型时，ΨPO 的最优策略与 RLHF 和 DPO 的最优策略完全一致（命题1）。这表明 DPO 和 RLHF 都是这个通用框架下的特例。

DPO/RLHF 的问题：弱正则化与过拟合

本文的核心洞察在于，DPO 和 RLHF 所依赖的 BT 模型假设是其脆弱性的根源。

BT 模型将偏好概率表示为 \(p(y > y') = σ(r(y) - r(y'))\)。当一个选项 \(y\) 总是优于另一个选项 \(y'\) 时（即 \(p*(y > y')=1\)），为了拟合这个确定性偏好，BT 模型要求奖励差异 \(r(y) - r(y')\) 趋向于正无穷。

在 DPO 和 RLHF 的最优策略 \(π*\) 的闭式解中，策略概率与 \(exp(reward/τ)\) 成正比。当奖励差异趋于无穷时，无论 \(τ\) 取多大，KL 正则化项的影响都会被无限放大的奖励信号所淹没，导致最优策略 \(π*\) 会将所有概率分配给获胜的选项，完全忽略了参考策略 \(π_ref\)。

在实际应用中，即使真实偏好不是确定性的，但在有限数据下，我们观察到的经验偏好很可能为1或0，从而触发这种过拟合。DPO 由于直接优化，更容易受到此问题影响。而 RLHF 在实践中可能通过对奖励模型的“欠拟合”（underfitting）和正则化（如早停）来隐式地缓解这个问题。

新方法：IPO

为了解决上述问题，本文提出选择一个有界的 \(Ψ\) 函数，以确保 KL 正则化项在任何情况下都有效。最自然的选择是令 \(Ψ\) 为恒等映射，即 \(Ψ(p) = p\)，这便得到了恒等偏好优化 (Identity-PO, IPO) 方法。

IPO 的目标是直接最大化策略的期望偏好，同时受 KL 正则化约束。因为它不依赖于将偏好转化为无界奖励的 BT 模型，所以即使在面对确定性偏好时，正则化项 \(τ\) 依然能有效控制策略与参考策略的距离，从而避免了 DPO 的过拟合问题。

IPO 的优化算法

为了让 IPO 能够直接从偏好数据中进行端到端的训练，本文推导出了一个高效的离线学习损失函数。

1. 构建优化问题：与 DPO 的推导类似，首先将 IPO 的最优解条件转化为一个关于策略 \(π\) 的方程组求解问题。然后，将这个方程组问题转化为一个最小化均方误差的优化问题 \(L(π)\)：

   \[L(\pi) = \underset{y, y' \sim \mu}{\mathbb{E}} \left[ \left( h_{\pi}(y, y') - \frac{p^*(y \succ \mu) - p^*(y' \succ \mu)}{\tau} \right)^2 \right]\]

   其中 \(h_π\) 表示策略 \(π\) 和参考策略 \(π_ref\) 的对数概率比之差。

2. 唯一最优解：本文证明了（定理2）该损失函数 \(L(π)\) 是凸的，并且在策略空间中存在唯一的全局最优解 \(π*\)，这保证了优化过程的稳定性。

3. 推导可采样的损失函数：上述 \(L(π)\) 依赖于真实的期望偏好 \(p*\)，无法直接从样本计算。通过巧妙的数学变换（命题3），本文证明 \(L(π)\) 等价于一个可以使用样本进行无偏估计的损失形式。最终，对于一个偏好数据点 \((y_w, y_l)\)（\(y_w\) 是获胜者，\(y_l\) 是失败者），IPO 的最终采样损失函数可以简化为：

   \[\mathcal{L}_{IPO}(\pi) = \left( h_\pi(y_w, y_l) - \frac{1}{2\tau} \right)^2\]

   其中 $$h_\pi(y_w, y_l) = \log(\frac{\pi(y_w

   x)}{\pi(y_l

   x)}) - \log(\frac{\pi_{ref}(y_w

   x)}{\pi_{ref}(y_l

   x)})\(。这个损失函数形式简洁，其实质是将策略对数概率比与参考策略对数概率比的差值，回归到一个由正则化系数\)τ$$ 控制的常数上。这直观地体现了 IPO 如何通过控制策略的相对变化来避免过拟合。

实验结论

本文通过一系列简单的 bandit 示例，清晰地展示了 IPO 相对于 DPO 的优势。

• 确定性偏好下的表现：在只有两个动作且偏好是确定的（\(p*(y1 > y2) = 1\)）的场景下，DPO 无论正则化系数 \(τ\) 多大，其策略都会收敛到确定性策略 \(π(y1)=1\)。而 IPO 的策略则会根据 \(τ\) 的大小平滑地在参考策略 \(π_ref\) 和确定性策略之间过渡，\(τ\) 真正起到了控制正则化强度的作用。

• 样本偏好下的过拟合：实验在一个三动作空间中进行，使用有限的偏好样本。
  • 场景一（总有胜者）：当一个动作 \(ya\) 在所有观测样本中都获胜时，DPO 的策略迅速收敛到 \(π(ya)=1\)，完全忽略了 \(τ\) 和参考策略。相比之下，IPO 的策略则保持了对 \(τ\) 的敏感性，当 \(τ\) 较大时，策略能有效保持与参考策略的接近。

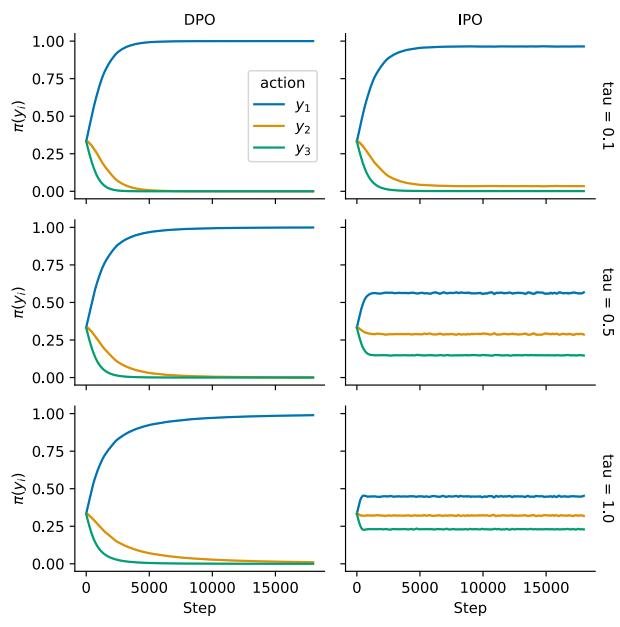  图1：在数据集D1上的IPO和DPO动作概率学习曲线比较

  • 场景二（总有败者或未见胜者）：当一个动作 \(yc\) 在观测样本中从未获胜时，DPO 会将其概率降为0，同样不受 \(τ\) 的影响。这种行为在动作空间大而数据集小的情况下尤其危险。而 IPO 则会根据 \(τ\) 的值，逐步、可控地降低该动作的概率，表现得更为稳健。

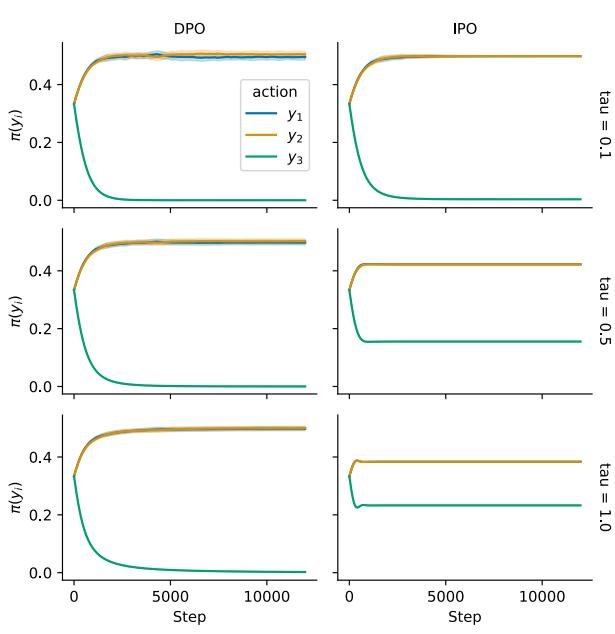  图2：在数据集D3上的IPO和DPO动作概率学习曲线比较

• 最终结论：实验结果有力地证实了理论分析：DPO 在面对确定性或稀疏的偏好数据时存在固有的不稳定性，容易忽略正则化项并过拟合到观测数据上。而本文提出的 IPO 方法通过绕开 BT 模型假设，在各种情况下都表现出更好的稳定性和对正则化系数的遵循，能够有效避免过拟合，是一种更可靠的从人类偏好中学习的算法。未来的工作应将 IPO 的实验扩展到更复杂的任务，如在真实的人类偏好数据上训练大型语言模型。