A Novel Combined Data-Driven Approach for Electricity Theft Detection

TL;DR

本文提出了一种结合最大信息系数(MIC)和快速搜索密度峰值聚类(CFSFDP)的数据驱动方法，以无监督的方式，仅需少量额外信息（区域总电表数据），即可高效、准确地检测出形态各异的电力盗窃行为。

关键定义

相关工作

电力盗窃检测方法主要分为三类：基于人工智能（AI）的方法、基于状态（state-based）的方法和基于博弈论的方法。

本文方法

本文提出一个结合了两种互补数据挖掘技术的组合检测框架，分别从“幅度-相关性”和“形状-相似性”两个维度量化用户的窃电嫌疑。

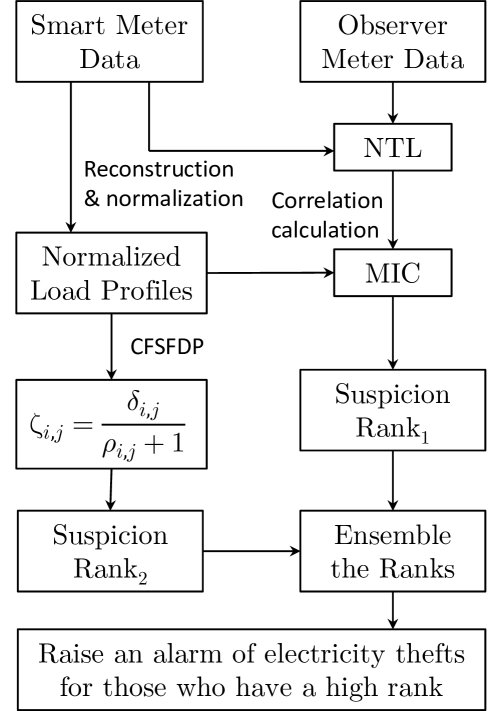图：MIC-CFSFDP组合检测框架

创新点

该框架的创新在于将两种先进技术进行优势互补：

  1. 基于MIC的相关性检测：用于发现那些用电曲线形状正常、但用电量与区域NTL存在强相关性的窃电行为。
  2. 基于CFSFDP的异常检测：用于发现那些用电曲线形状被篡改得非常规、无规律的窃电行为。

通过结合两种方法的排序结果，该框架能够覆盖更多样的窃电手段，从而提高检测的准确性和鲁棒性。

基于最大信息系数（MIC）的相关性检测

该方法基于一个核心假设：窃电用户的用电行为与区域的非技术性损失（NTL）存在关联。

  1. 计算NTL：在一个安装了安全观察电表的区域内，NTL可以通过观察电表的总读数 $E_t$ 减去该区域所有用户智能电表读数 $\tilde{x}_{i,t}$ 的总和来计算：

    \[e_{t}=E_{t}-\sum_{i\in\mathcal{A}}\tilde{x}_{i,t}\]

    理论上，这个NTL $e_t$ 主要由窃电用户的窃电量构成。

  2. 关联性假设：如果一个窃电用户 $i$ 篡改后的电量 $\tilde{x}_{i,t}$ 与其真实用电量 $x_{i,t}$ 仍保持一定关系（如按比例减少），那么其窃电量 $(x_{i,t}-\tilde{x}_{i,t})$ 也会与 $\tilde{x}_{i,t}$ 相关。因此，区域总NTL序列 e 与窃电用户 $i$ 的用电序列 $\tilde{\textbf{x}}_{i}$ 之间的相关性会显著高于正常用户：

    \[Corr(\textbf{e},\tilde{\textbf{x}}_{i})\Big{ \mid }_{i\in\mathcal{F}} > Corr(\textbf{e},\tilde{\textbf{x}}_{i})\Big{ \mid }_{i\in\mathcal{B}}\]

    其中 $\mathcal{F}$ 是窃电用户集合，$\mathcal{B}$ 是正常用户集合。

  3. 采用MIC：传统的皮尔逊相关系数（PCC）只能检测线性关系。而窃电行为可能更复杂，因此本文采用MIC作为相关性度量 $Corr(\cdot, \cdot)$，因为它能有效捕捉线性和非线性关联。MIC值越高，表明该用户是窃电用户的嫌疑越大。

基于CFSFDP的无监督异常检测

对于某些窃电类型（如随机降低用电量），其篡改后的用电曲线与原始曲线关联性弱，导致MIC方法失效。但这类行为往往会产生形状异常的负载曲线，使其成为数据分布中的“异常点”。

  1. CFSFDP原理：该算法为每个数据点（这里指每日的负载曲线）计算两个关键指标：
    • 局部密度 $\rho_{p}$：点 $p$ 周围邻居点的数量。
    • 相对距离 $\delta_{p}$：点 $p$ 与比它密度更高的点中最近那一个的距离。

  2. 识别异常点：异常点通常远离数据密集的区域，表现为低密度 $\rho_{p}$ 和高距离 $\delta_{p}$。

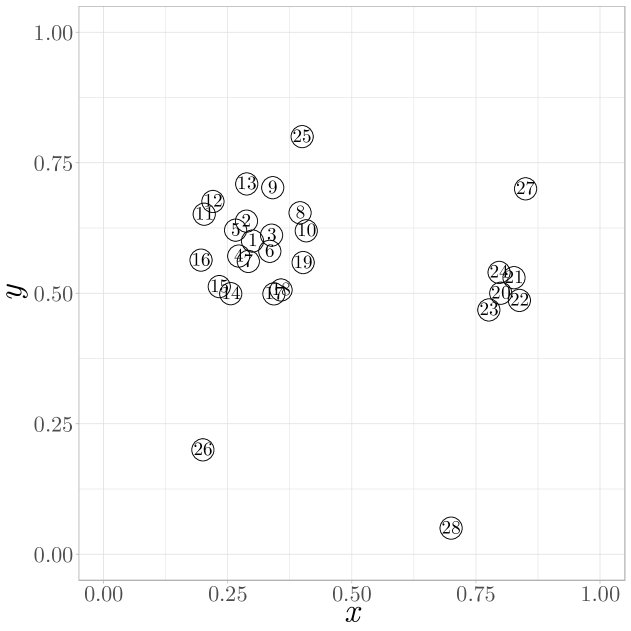    图：数据点分布示例，#26~28为异常点

    图：示例数据点的(ρ, δ)散点图

  3. 计算异常度：本文定义了一个“异常度”指标 $\zeta_{p}$ 来量化每个负载曲线的异常程度：

    \[\zeta_{p}=\frac{\delta_{p}}{\rho_{p}+1}\]

    $\zeta_{p}$ 值越高的用户，其用电曲线形状越可疑。

组合检测框架

该框架将上述两种方法的结果进行融合，得出最终的嫌疑排名。

  1. 数据预处理：将每个用户每天的负载曲线进行归一化，以专注于形状特征。
  2. 计算嫌疑度：
    • 对每个用户每天的归一化曲线，分别计算其与当天NTL的MIC值。
    • 在所有日负载曲线数据集中，计算每条曲线的CFSFDP异常度 $\zeta$ 值。
    • 对每个用户，将其多天的MIC值（或$\zeta$值）通过k-means聚类（k=2）分为“正常”和“可疑”两组，取“可疑”组的均值作为该用户的最终MIC嫌疑度（或CFSFDP嫌疑度）。

  3. 融合排名：根据两种嫌疑度分别对所有用户进行排名，得到 $Rank_1$ (来自MIC) 和 $Rank_2$ (来自CFSFDP)。然后使用算术平均或几何平均来合并这两个排名，得到最终的综合排名：

    \[\begin{split} &Rank_{\text{Arith}}=\frac{Rank_{1}+Rank_{2}}{2}\\ \text{or } &Rank_{\text{Geo}}=\sqrt{Rank_{1}\times Rank_{2}} \end{split}\]

综合排名高的用户被认为是重点怀疑对象。

实验结论

实验在包含5000多用户的爱尔兰智能电表数据集上进行，模拟了6种不同的虚假数据注入（FDI）类型来代表窃电行为。

图：6种FDI窃电类型示例

类型 修改方式
FDI1 $\tilde{x}_{t}\leftarrow\alpha x_{t}$ (按比例减少)
FDI2 $\tilde{x}_{t}\leftarrow\min(x_t, \gamma)$ (削峰)
FDI3 $\tilde{x}_{t}\leftarrow\max(x_t - \gamma, 0)$ (整体降低)
FDI4 $\tilde{x}_{t}\leftarrow f(t)\cdot x_{t}$ (某时段清零)
FDI5 $\tilde{x}_{t}\leftarrow\alpha_{t}x_{t}$ (随机比例减少)
FDI6 $\tilde{x}_{t}\leftarrow\alpha_{t}\bar{\textbf{x}}$ (随机常数)

表：六种FDI（虚假数据注入）类型定义

类型 AUC(%)   MAP@20(%)      
  MIC CFSFDP Arith MIC CFSFDP Arith
FDI1 92.7 49.5 76.6 90.6 20.2 69.6
FDI2 70.3 55.7 72.5 69.5 34.3 51.5
FDI3 67.2 68.3 78.7 59.4 39.6 66.8
FDI4 86.1 85.3 96.0 80.4 35.4 97.5
FDI5 59.9 86.0 85.1 53.3 32.3 81.0
FDI6 38.6 97.9 81.2 7.8 57.4 73.1
MIX 66.2 74.8 81.6 69.3 52.6 83.1

表：不同方法在各类FDI上的性能对比（节选）