Allocation of Parameters in Transformers
-
ArXiv URL: http://arxiv.org/abs/2510.03784v1
-
作者: Ruoxi Yu; Zhong Li; Jingpu Cheng; Qianxiao Li; Haotian Jiang
-
发布机构: Center for Data Science; Institute for Functional Intelligent Materials; Microsoft Research Asia; National University of Singapore; Peking University
TL;DR
本文通过数学分析 Transformer 模型中参数分配的效率,从理论上揭示了对于信息提取任务,早期层中的注意力头数量与头维度之间存在权衡关系,并证明了 Softmax 激活函数存在饱和效应,这为后期层减少参数提供了理论依据,最终提出了跨层优化参数(注意力和头维度)分配的原则性策略。
关键定义
本文提出或重点阐释了以下核心概念:
-
信息提取中的参数权衡 (Parameter Trade-off in Information Extraction):在 Transformer 的早期层中,给定固定的总参数预算(如模型嵌入维度 $D$),注意力的头数量 (\(head\)) 与每个头的维度 (\(dim\)) 之间存在一种权衡。增加头维度有利于更完整地保留单个 token 的信息,而增加头的数量则有助于更精确地学习token之间的组合关系。本文通过构建近似误差上界,从数学上量化了这种权衡关系。
-
Softmax 饱和效应 (Softmax Saturation):指 Softmax 激活函数的输出对输入(logits)的敏感度随着序列长度的增加而降低的现象。本文从理论上证明,Softmax 输出关于其输入的雅可比矩阵的谱范数与序列长度 $L$ 成反比,即 $\mathcal{O}(1/L)$。这意味着对于长序列,即使 logits 有较大变化,注意力分数的改变量也很小。这种饱和行为表明,在后期层或处理长序列时,可以适当减小头的维度而不会显著影响模型性能,从而实现参数削减。
相关工作
尽管 Transformer 架构在自然语言处理、计算机视觉等领域取得了巨大成功,但其模型效率的理论基础仍不完善。现有研究通过实验和可视化分析发现,Transformer 的不同层存在功能分工:浅层倾向于编码表层和 token 级别的特征,而深层则侧重于捕捉抽象的句法和语义信息。然而,领域内仍然缺乏一个严谨的理论框架来解释如何高效地分配模型参数(主要是注意力头的数量和每个头的维度),以平衡模型的表达能力和计算效率。
本文旨在解决的核心问题是:在给定的总参数预算下,应如何在 Transformer 的不同层之间分配注意力头和头维度,才能实现理论上最优的模型效率?这不仅有助于加深对 Transformer 工作机制的理解,也能为设计更高效的模型架构提供原则性指导。
本文方法
本文从理论上分析了 Transformer 模型中参数分配的效率,提出了两个核心洞见,并基于此给出了参数分配策略。
信息提取中的参数权衡
本文首先关注 Transformer 的浅层,这些层主要负责执行信息提取任务。作者将这类任务形式化为学习输入 token 的线性组合,即一个序列到序列的卷积操作:$\mathbf{y}_{t}=\sum_{i=0}^{L}\mathbf{\rho}_{i}\mathbf{x}_{t-i}$。
在此设定下,作者推导了单层 Transformer 在固定嵌入维度 $D$ 下的近似误差 $\mathcal{E}_{D}(\mathbf{X})$ 的上界。
\[\mathcal{E}\_{D}(\mathbf{X})\leq\sum\_{m=1}^{M}\ \mid \mathbf{\rho}\_{m}\ \mid \_{2}B\left((1+\varepsilon\_{\delta})\mathbb{I}\_{\left\{d\_{m}\leq d\right\}}\sqrt{1-\frac{d\_{m}}{d}}+\frac{1.3\ e^{0.02m}}{H\_{m}}\right)+\sum\_{k=M+1}^{L}\ \mid \mathbf{\rho}\_{k}\ \mid \_{2}B\]这个误差界包含两个关键部分:
- 维度保留误差:第一项 $\sqrt{1-\frac{d_{m}}{d}}$ 随着头维度 $d_m$ 的增大而减小。这反映了更大的头维度能够更好地保留原始 token 的信息,减少因维度压缩带来的损失。
- 函数近似误差:第二项 $\frac{1.3\ e^{0.02m}}{H_{m}}$ 随着头数量 $H_m$ 的增多而减小。这表示使用更多的注意力头可以更精确地逼近目标线性组合函数。
创新点: 该理论首次从数学上揭示并量化了在固定参数预算 $D = \sum H_m \cdot d_m$ 的约束下,头数量 $H_m$ 和头维度 $d_m$ 之间的内在权衡。为了最小化总误差,必须在这两者之间找到一个最佳平衡点。这为浅层参数分配提供了一个原则性的优化目标,而非依赖经验性的试错。
基于此,作者提出了一个优化问题来指导参数分配:
| (通过权衡进行参数分配) | ||
|---|---|---|
| $\min_{M,H_{m},d_{m}}$ | $\quad\sum_{m=1}^{M}\ \mid \mathbf{\rho}_{m}\ \mid _{2}B\left(\mathbb{I}_{\left{d_{m}\leq d\right}}\sqrt{1-\frac{d_{m}}{d}}+\frac{1.3\ e^{0.02m}}{H_{m}}\right)+\sum_{k=M+1}^{L}\ \mid \mathbf{\rho}_{k}\ \mid _{2}B,$ | |
| $\mathrm{s.t.}$ | $\quad\sum_{m=1}^{M}H_{m}\cdot d_{m}=D.$ |
该方法可以应用于具体的任务,如 N-gram 建模和实现归纳头 (Induction Head) 的第一步,甚至可以扩展到非线性序列建模。
Softmax饱和效应与参数削减
接下来,本文转向 Transformer 的中后期层。这些层通常只依赖少数几个主导的注意力头来处理更抽象的信息。作者从理论上证明了 Softmax 激活函数存在“饱和效应”,为在这些层中减少头维度提供了依据。
核心理论 (定理 2): 作者证明了注意力分数对 logits 的雅可比矩阵 $J_l$ 的谱范数满足:
\[\left\ \mid J\_{l}\right\ \mid \_{2}=\mathcal{O}\left(\frac{1}{L}\right),\quad l=1,2,\ldots,L,\]其中 $L$ 是序列长度。
优点: 这个结论表明,当序列很长时,Softmax 的输出对输入的微小变化不敏感,其“斜率”非常平坦。进一步推论(推论 2)得出,使用一个低维度的头来近似一个高维度的头,所产生的注意力分数误差很小,为 $\mathcal{O}\left(\frac{\Lambda_{h}^{H}}{L}\right)$。
这一发现的创新点在于为模型压缩和效率提升提供了坚实的理论基础。它表明,特别是在处理长序列的场景下,可以显著减小中后期层的头维度而不会严重影响模型性能。
基于此,本文提出了一种实用的参数削减策略:对于一个预训练好的模型,可以将其中的高维度注意力头(教师头)用一个低维度的头(学生头)来近似。具体步骤包括:
- 通过对教师头参数矩阵进行截断奇异值分解 (truncated SVD) 来初始化学生头的参数。
- 对学生头的参数进行进一步微调。
这种方法能够在保持模型性能的同时,实现有效的模型压缩。
实验结论
本文通过一系列数值实验验证了其理论发现。
信息提取中的参数权衡
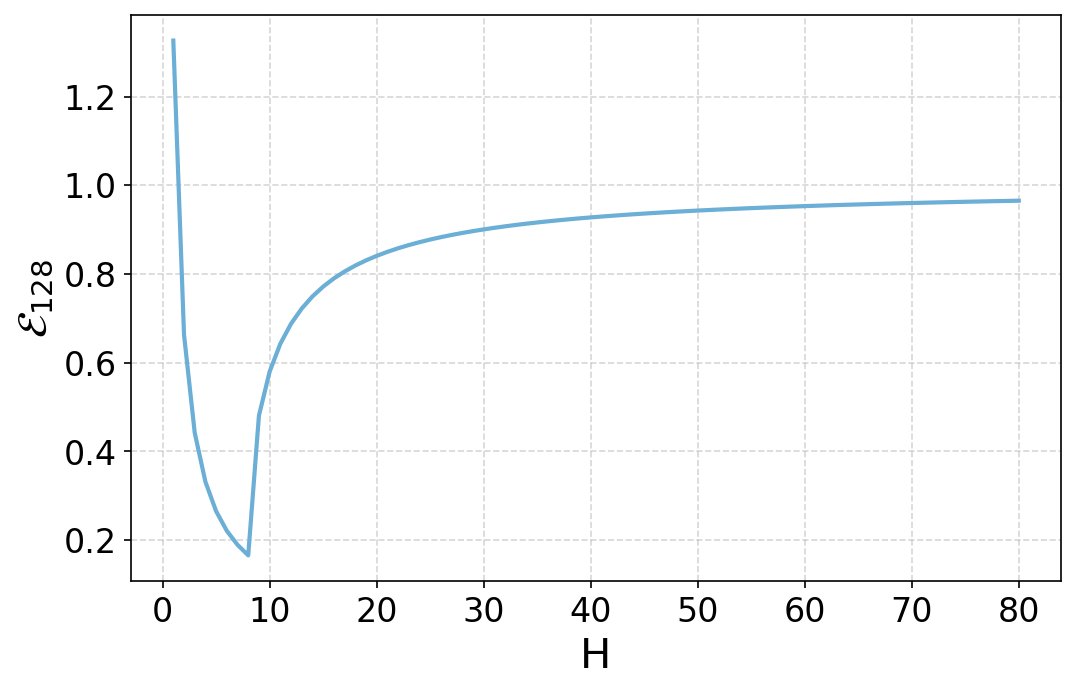
- 权衡趋势验证:实验首先绘制了理论误差界 $\mathcal{E}_{128}$ 随头数量 $H$ 变化的曲线。如下图所示,曲线呈现出明显的U形,证实了头数量和头维度之间的权衡关系。理论上的最优头数量在 $H=8$ 附近,与曲线的最低点吻合。
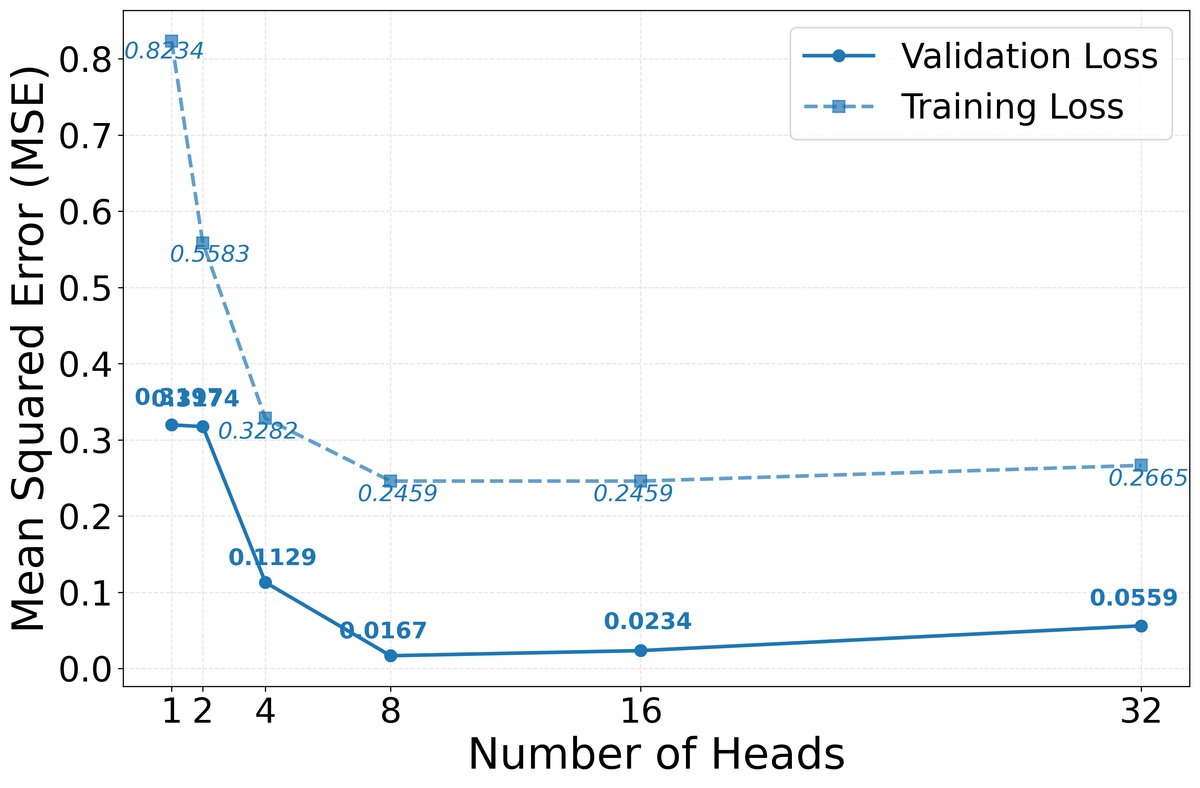
- 4-gram 任务验证:在一个合成的 4-gram 任务中,实验固定总嵌入维度 $D=256$,并测试了不同的头数量和维度组合。如下图所示,实验结果表明,当参数配置为 $M=4, d_m=8, H_m=8$ 时,模型取得了最低的测试误差。这一经验最优配置与通过理论优化问题(公式 5)求解得到的结果完全一致,验证了所提参数分配策略的有效性。
Softmax饱和效应与参数削减
- 雅可比范数与序列长度:实验分析了在 Wikitext-103 数据集上,注意力 Softmax 输出的雅可比矩阵谱范数如何随序列长度 $L$ 变化。结果显示,随着 $L$ 从4增加到1024,雅可比范数呈现出明显的下降趋势,这与理论上 $\mathcal{O}(1/L)$ 的结论(定理 2)相符。
- 单头压缩验证:实验对一个预训练 Transformer 模型中的单个注意力头(教师头)进行了压缩。结果表明,一个维度大大减小(如从64维降至4维)的学生头,通过 SVD 初始化和微调后,能够很好地近似教师头的行为。这证实了 Softmax 饱和效应的实际影响,并验证了基于该理论的参数削减策略的可行性和有效性。
综上所述,实验结果有力地支持了本文提出的两个核心理论:早期层中的参数权衡和后期层中的 Softmax 饱和效应,并证明了基于这些理论的参数分配与削减策略是有效且具有实践指导意义的。