BEFT: Bias-Efficient Fine-Tuning of Language Models

• ArXiv URL: http://arxiv.org/abs/2509.15974v1

• 作者: Ananth Balashankar; Amir Aminifar; Baichuan Huang

• 发布机构: Google DeepMind; Lund University

---

TL;DR

本文提出了一种偏置高效微调方法 (Bias-Efficient Fine-Tuning, BEFT)，其核心是一种通过计算微调前后偏置向量的投影比率来评估重要性的新方法，从而能够更精确地选择出对下游任务最关键的偏置项（如Q/K/V投影中的偏置）进行微调，以极低的参数量实现卓越性能。

关键定义

本文的核心创新在于提出了一种新的重要性评分方法来选择最优的偏置项。

• 重要性评分 (Importance Score): 本文定义了一个度量标准 $\mathcal{I}(\boldsymbol{b}_{\mathcal{T}})$，用于评估特定类型的偏置项 $\boldsymbol{b}_{\mathcal{T}}$（例如，来自查询\(q\)、键\(k\)或值\(v\)投影的偏置）在微调过程中的变化程度。该评分通过计算微调前后的偏置向量的投影比率得出，与仅考虑幅度或梯度的传统方法不同，它同时考虑了向量的角度和幅度变化。其计算公式为：

  \[\mathcal{I}(\boldsymbol{b}_{\mathcal{T}})=\frac{1}{L}\sum_{l=1}^{L}\left(1-\frac{\boldsymbol{b}^{(l),pre}_{\mathcal{T}}\cdot\boldsymbol{b}^{(l),post}_{\mathcal{T}}}{\max\left(\ \mid \boldsymbol{b}^{(l),pre}_{\mathcal{T}}\ \mid ^{2}_{2},\ \mid \boldsymbol{b}^{(l),post}_{\mathcal{T}}\ \mid ^{2}_{2}\right)}\right)\]

  其中，$\boldsymbol{b}^{(l),pre}_{\mathcal{T}}$ 和 $\boldsymbol{b}^{(l),post}_{\mathcal{T}}$ 分别表示第 $l$ 层微调前后的偏置向量。得分越高，表示该偏置项变化越大，越重要。

相关工作

目前，参数高效微调 (Parameter-Efficient Fine-Tuning, PEFT) 技术旨在减少微调大型语言模型时的计算开销。其中，仅微调偏置项 (bias-only fine-tuning) 是一种极具潜力的方法，它无需额外模块，在低数据场景下表现优异。

然而，现有工作存在一个关键瓶颈：对于Transformer中的不同偏置项（如查询\(q\)、键\(k\)、值\(v\)投影中的偏置），如何选择最有效的一个进行微调尚不明确。先前的方法，如基于偏置变化幅度 (Magnitude) 或费雪信息 (Fisher information) 的方法，在指导选择时存在局限性，无法精确、动态地识别出最优偏置项。

本文旨在解决这个具体问题：如何精确地选择一个特定的偏置项进行微调，以实现最高的参数效率和性能。

本文方法

创新点

本文提出了一种新的偏置选择方法，为偏置高效微调 (BEFT) 奠定了基础。其核心创新在于使用微调前后偏置向量的投影比率来共同衡量其角度和幅度的变化，从而更精确地评估每个偏置项的重要性。

具体来说，给定微调前的偏置向量 $\boldsymbol{b}^{pre}$ 和微调后的向量 $\boldsymbol{b}^{post}$，该方法：

1. 计算两个向量的点积，这包含了它们之间的角度信息。
2. 用点积除以两个向量中范数较大者的平方，实现了对变化的归一化。这确保了无论向量是变长还是变短，度量都保持一致和公平。
3. 通过从1中减去该比率，得到最终的重要性分数。变化越大，该比率越小，最终得分越高。

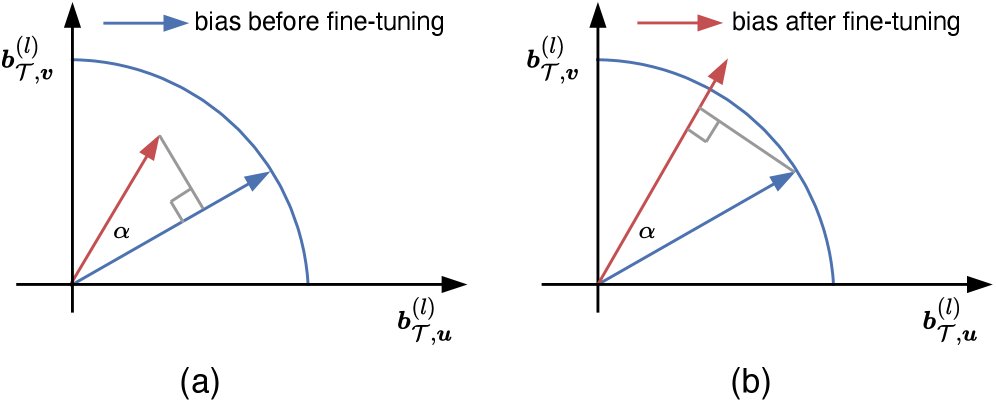图：本文的偏置高效方法同时考虑了角度和幅度的变化，计算 $\boldsymbol{b}_{\mathcal{T}}^{(l)}$ 的投影比率。

优点

与现有方法相比，本文提出的度量方式具有明显优势：

• 克服了“幅度”方法的局限性：基于幅度的度量（如L1或L2范数）无法区分方向不同但变化量相同的更新。如下图(a)所示，位于绿色菱形上的所有终点，其幅度变化相同，但本文方法可以区分它们。
• 克服了“费雪信息”方法的局限性：基于费雪信息的方法依赖于梯度平方，无法区分方向不同但梯度模长相同的更新。如下图(b)所示，位于黄色圆上的所有梯度，其费雪信息值相同。此外，费雪信息在训练中往往是静态的。
• 精确与动态：本文方法（图c）通过联合考虑角度和幅度，提供了一个更精细和动态的度量，能够捕捉到其他方法忽略的细微但重要的变化，从而更准确地识别出对下游任务性能影响最大的偏置项。

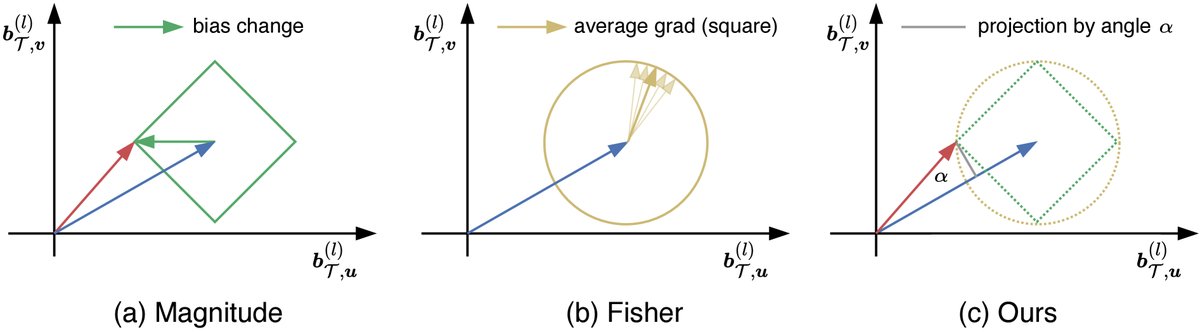图：三种偏置选择方法的对比。(a) 幅度法：绿色菱形上的点具有相同的L1范数变化。(b) 费雪信息法：黄色圆上的点具有相同的梯度平方和。(c) 本文方法：克服了前两者的局限性。

最终，通过计算所有偏置类型（\(q\)、\(k\)、\(v\)）的重要性分数，本文选择得分最高的类型进行微调：

\[\mathcal{T}=\underset{\mathcal{T}\in\{q,\ k,\ v\}}{\arg\max}{\{\mathcal{I}(\boldsymbol{b}_{\mathcal{T}})\}}\]

实验结论

本文通过在编码器（BERT、RoBERTa）和解码器（OPT-1.3B、OPT-6.7B）等多种模型和任务上进行广泛实验，验证了所提方法的有效性。

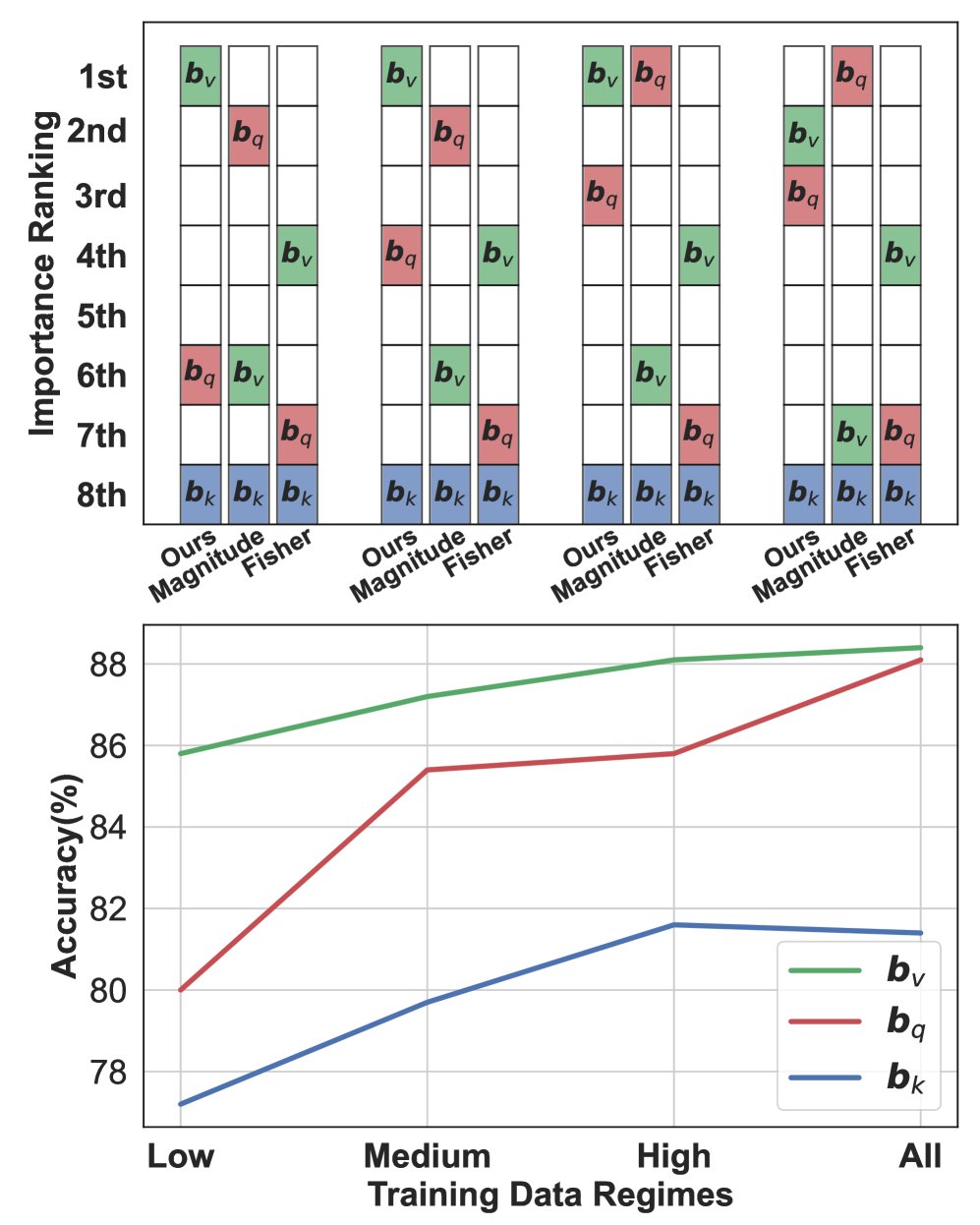SST-2

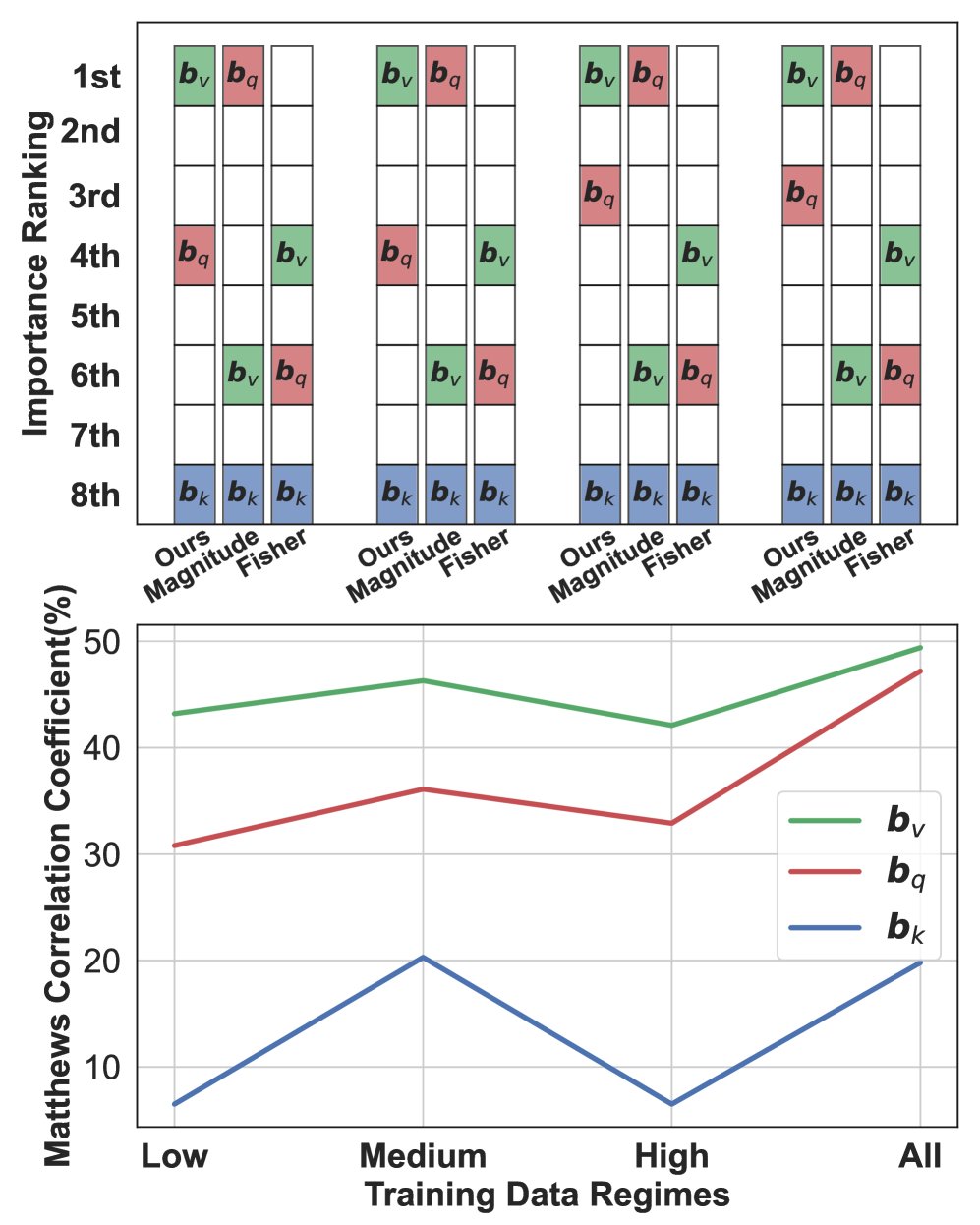CoLA

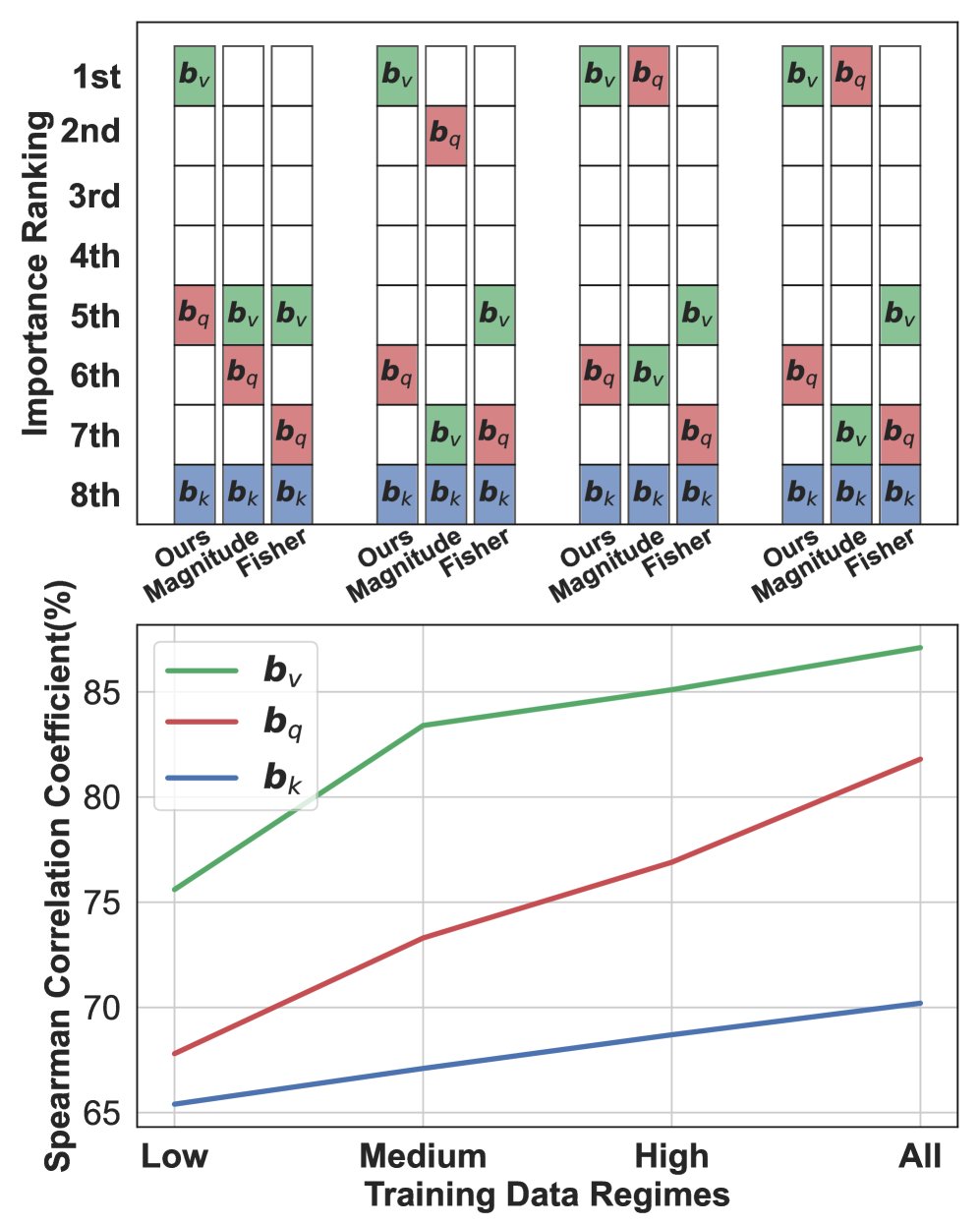STS-B 图：在BERT模型上，本文方法能精确动态地选择最优偏置项，性能优于Magnitude和Fisher方法。

核心发现

• 选择准确性：本文提出的方法能够一致且准确地识别出最重要的偏置项（通常是值偏置 $\boldsymbol{b}_{v}$），其选择结果与下游任务的实际性能高度相关，显著优于Magnitude和Fisher方法。如上图所示，在SST-2、CoLA和STS-B任务中，本文方法选择的偏置项（通常是$\boldsymbol{b}_{v}$）均取得了最高性能，而其他方法则常常做出错误选择。

• 高效率与高性能：本文的BEFT方法（即仅微调选出的最优偏置项）表现出卓越的效率。例如，在RTE任务上微调BERT，BEFT仅需训练0.01%的参数，训练时间也更短，但其性能与训练所有偏置（0.09%参数）甚至全参数微调相当。

微调方法	可训练参数↓	运行时间(s)↓	准确率↑
本文方法 (BEFT)	0.01%	132.9	58.53±1.88
随机均匀选择	0.01%	134.6	50.40±2.94
所有偏置	0.09%	144.9	56.40±2.88
全参数	100%	206.1	57.46±2.20

• 泛化能力强：实验证明，”微调值偏置$\boldsymbol{b}_{v}$”这一发现具有很强的泛化性。
  • 跨模型泛化：从BERT到RoBERTa，再到高达6.7B参数的自回归模型OPT，微调$\boldsymbol{b}_{v}$始终是最佳选择。
  • 跨任务泛化：该结论在分类、多选和生成等多种任务类型中均成立。
  • 与主流方法对比：在大型模型上，仅微调$\boldsymbol{b}_{v}$的BEFT方法，其参数量比LoRA少30倍，比Prefix Tuning少10倍，但在大多数任务上取得了有竞争力甚至更优的性能。

适应技术	SST-2	RTE	CB	WiC	SQuAD	DROP
本文方法 (仅微调 $\boldsymbol{b}_{v}$)	88.6	68.2	85.7	67.0	87.2	37.0
LoRA	89.6	70.0	85.7	66.8	87.5	38.0
Prefix Tuning	89.2	68.6	82.1	68.0	87.2	34.3
In-Context Learning ( few-shot)	85.6	53.8	62.5	49.3	70.9	22.8
Zero-shot	84.7	56.7	53.6	50.3	55.4	14.8

最终结论

本文成功提出了一种新颖、精确的偏置项选择方法。基于此方法的BEFT在仅微调极少量参数（通常是值偏置$\boldsymbol{b}_{v}$）的情况下，实现了与全量微调及其他主流PEFT方法相媲美的性能，展示了其作为一种前所未有的参数高效微调策略的巨大潜力。

局限性

本文虽然揭示了选择特定偏置项的重要性，并提供了一个有效的选择方法，但对于该重要性分数与下游性能之间的定量关系，仍需未来工作进行更深入的探究。