Behind RoPE: How Does Causal Mask Encode Positional Information?

TL;DR

本文通过理论证明和实验分析，揭示了Transformer解码器中的因果掩码 (Causal Mask) 本身就是一种位置信息来源，它能诱导出偏好邻近token的注意力模式，并且会与RoPE等显式位置编码相互作用，将其相对注意力模式扭曲为非相对模式。

关键定义

本文主要对现有概念进行了深入的理论剖析，而非提出全新定义。其核心在于重新定义了对以下概念的理解：

相关工作

目前，为Transformer注入位置信息的主流方法是使用显式的位置编码 (Positional Encodings)。这些方法可分为两类：绝对位置编码（如正弦编码）和相对位置编码（如RoPE）。其中，RoPE因其优越的性能和对相对位置的建模能力，在现代大语言模型 (LLM) 中被广泛采用。

然而，近期研究发现，即使没有显式的位置编码，Transformer解码器依然能够处理序列数据，这表明模型中存在其他位置信息来源。研究者们推测因果掩码是关键，但其具体作用机制并不明确。有人假设它通过“计数”前面的token来编码位置，有人证明在特定参数下它可以模拟绝对和相对编码，还有人发现它会改变隐藏状态的方差或相似性。

本文旨在解决的核心问题是：因果掩码究竟是如何精确地编码位置信息的？ 本文通过数学推导，首次给出了一个清晰的机制解释，并进一步探究了它与RoPE在现代LLM中的相互作用。

本文方法

本文的核心贡献在于通过一个简化的、无参数的Transformer模型，从理论上证明了因果掩码的位置编码机制，并分析了其与RoPE的相互作用。

因果掩码如何编码位置信息？

本文证明，即使在没有模型参数、没有前馈网络 (FFN)、输入token之间没有因果依赖的极简设定下，仅因果掩码和多层注意力机制就能产生位置相关的注意力模式。

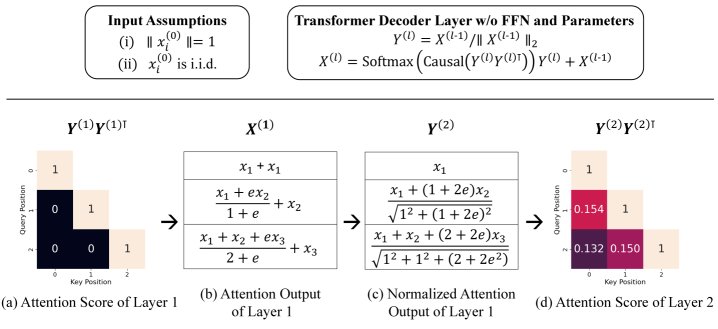
图1：因果掩码诱导位置信息的机制示意图

(a) 在特定的输入假设下，第一层的注意力分数在对角线上为1，其他位置为0。(b) 注意力输出是输入 $x_i^{(0)}$ 的加权和。(c) 经过 $\ell_2$ 归一化后，(d) 后续层的注意力分数展现出清晰的位置相关模式，给予邻近的查询-键对更高的权重，类似于常见的位置编码。

理论推导过程：

  1. 模型简化：考虑一个无参数、无FFN、使用行式 $\ell_2$ 归一化的Transformer层。其核心操作为：

    \[f(X)=\mathrm{Softmax}(\mathrm{Causal}(YY^{\top}))Y+X,\quad Y=\textrm{L2Norm}(X)\]

    假设输入向量 $x^{(0)}_i$ 具有单位范数，且任意不同向量间的期望内积为一个常数 $\alpha$（即 $\mathbb{E}(\langle x^{(0)}_{i},x^{(0)}_{j}\rangle)=\alpha$ for $i\neq j$）。

  2. 第一层分析：在第一层，由于输入是单位向量，归一化后的 $Y^{(1)} = X^{(0)}$。经过因果掩码和Softmax后，注意力输出 $x^{(1)}_i$ 成为其自身 $x^{(0)}_i$ 和所有先前token $x^{(0)}_k$ (for $k<i$) 的加权和。具体表达式为：

    \[x^{(1)}_{i}=\frac{(2e+(i-1)e^{\alpha})x^{(0)}_{i}+\sum_{k=1}^{i-1}e^{\alpha}x^{(0)}_{k}}{e+(i-1)e^{\alpha}}\]

    这个过程破坏了输入的对称性，使得每个位置的输出 $x^{(1)}_i$ 的构成都与其位置索引 $i$ 相关。

  3. 第二层的位置模式涌现：计算第二层归一化之前向量的内积 $\langle x_{i}^{(1)},x_{j}^{(1)}\rangle$ (假设 $i>j$)，可以推导出它是一个仅与索引 $i$ 相关的函数 $g(i)$：

    \[\langle x_{i}^{(1)},x_{j}^{(1)}\rangle = \frac{2\Big(2\alpha e+e^{\alpha}\big(1+\alpha(2i-3)\big)\Big)}{e+(i-1)e^{\alpha}}=g(i)\]

    同时，向量的范数平方 $ \mid \mid x_{i}^{(1)} \mid \mid _{2}^{2}$ 也是一个仅与索引 $i$ 相关的函数 $h(i)^2$。

  4. 核心结论：因此，第二层归一化后向量的内积（即第二层注意力的Pre-Softmax分数）为：

    \[\langle y^{(2)}_{i},y_{j}^{(2)}\rangle=\frac{\langle x^{(1)}_{i},x_{j}^{(1)}\rangle}{ \mid \mid x^{(1)}_{i} \mid \mid \_{2} \mid \mid x^{(1)}_{j} \mid \mid \_{2}}=\frac{g(i)}{h(i)h(j)}\]

    这个结果明确地显示，注意力分数是位置索引 $i$ 和 $j$ 的函数，证明了因果掩码本身能够诱导出位置相关性。

  5. 模式特性：进一步分析表明，函数 $h(j)$ 是关于 $j$ 的严格单调递减函数。因此，对于固定的查询位置 $i$，当键的位置 $j$ 越接近 $i$（即 $j$ 越大且 $j \le i$），$1/h(j)$ 的值越大，从而导致注意力分数 $\langle y^{(2)}_{i},y_{j}^{(2)}\rangle$ 越大。这说明因果掩码诱导的注意力模式天然地偏好关注更近的token，与RoPE等显式位置编码的行为类似。

因果掩码与RoPE的相互作用

本文进一步研究了当因果掩码与RoPE共同使用时的情况。RoPE的设计旨在使注意力分数仅依赖于相对距离 $(i-j)$。然而，本文的分析指出：

实验结论

无参数Transformer模拟

通过模拟一个无参数的Transformer解码器，实验验证了理论推导的正确性。

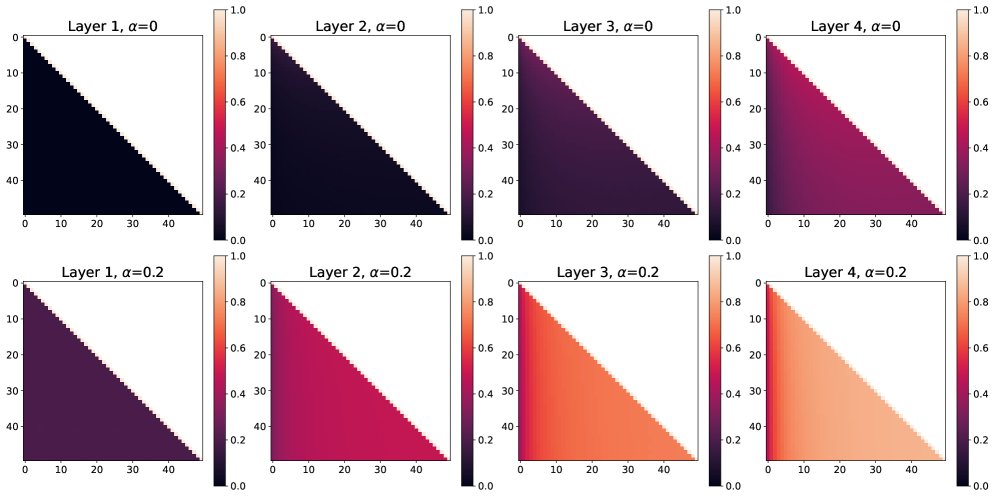
图2：无参数、无显式位置编码的Transformer模拟结果

(上排 $\alpha=0$, 下排 $\alpha=0.2$) 模拟显示，从第二层开始，注意力图中逐渐浮现出位置相关的模式。随着层数加深，查询关注邻近键的趋势愈发明显。$\alpha$ 的取值会影响模式的强度和饱和速度。

无位置编码的真实模型分析

本文训练了一个1.5B参数的Llama-3架构模型（无显式位置编码），并分析了其内部的注意力中间状态。

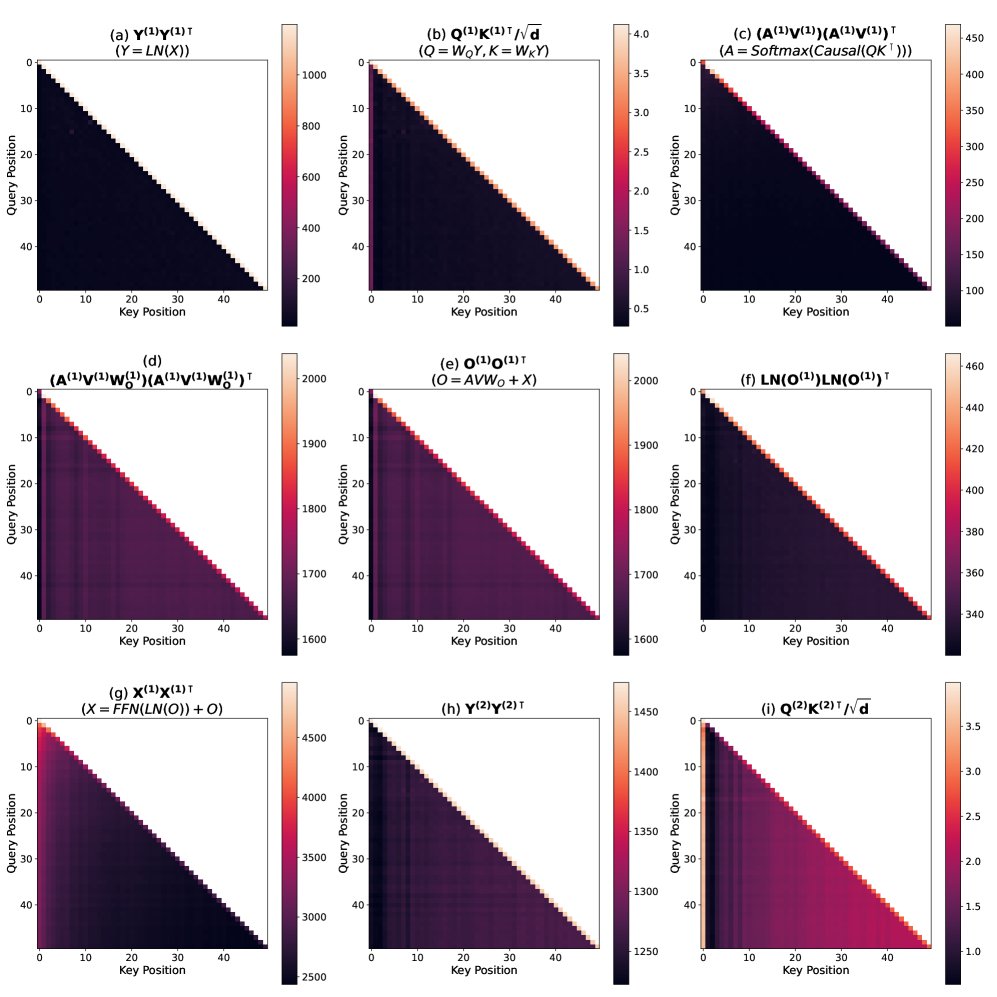
图3：无位置编码的已训练模型内部的内积格拉姆矩阵热力图

(a)到(i)展示了从输入嵌入到第二层注意力分数的演化过程。

因果掩码与RoPE的相互作用分析

模拟实验

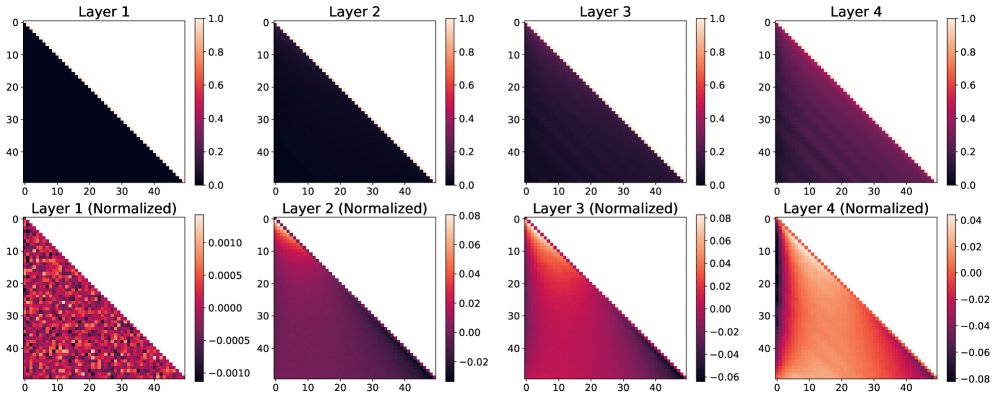
图4：使用RoPE的无参数Transformer模拟

(上排) 原始注意力分数。(下排) 减去对角线均值后的归一化分数，更清晰地揭示了非相对模式。

模拟实验在无参数模型中加入了RoPE。结果（图4）显示，从第二层开始，注意力图中出现了明显的非相对模式：靠近序列开头的区域（左侧）颜色更深，表示注意力分数系统性地偏低。这证实了因果掩码会扭曲RoPE的纯相对注意力。

现代LLM分析

本文分析了Llama-3.1 8B、Phi-4和Qwen3-8B等使用RoPE的现代LLM。

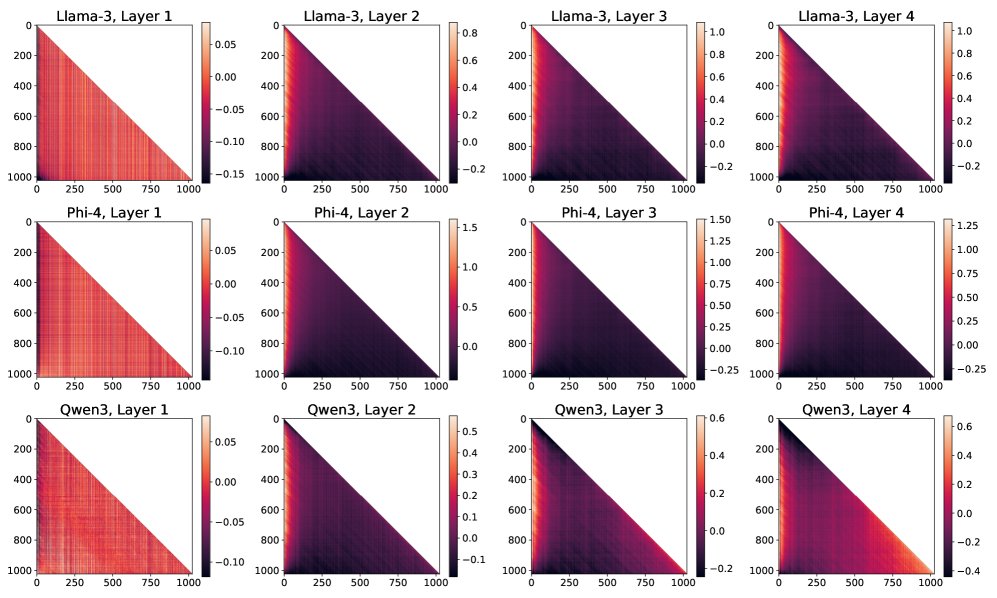
图5：真实LLM前4层的对角线归一化注意力热力图

各个模型的前几层普遍存在非相对模式，即注意力图左侧区域的值系统性偏低。