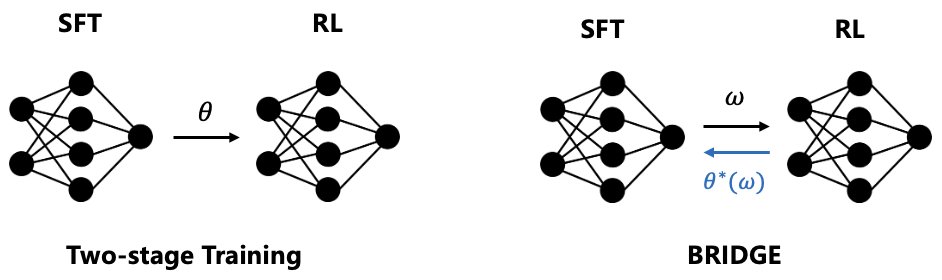
Beyond Two-Stage Training: Cooperative SFT and RL for LLM Reasoning

• ArXiv URL: http://arxiv.org/abs/2509.06948v1

• 作者: Xueting Han; Li Shen; Jing Bai; Kam-Fai Wong; Liang Chen

• 发布机构: Microsoft Research; Sun Yat-sen University; The Chinese University of Hong Kong

---

TL;DR

• 本文提出了一种名为 BRIDGE 的新型训练框架，它通过双层优化 (bilevel optimization) 将监督微调 (SFT) 和强化学习 (RL) 紧密结合，从而超越传统的两阶段训练范式，更高效、更有效地提升大语言模型的推理能力。

关键定义

本文的核心是提出了一种新的训练框架，其关键概念根植于双层优化理论：

• 双层优化框架 (Bilevel Optimization Framework)：本文将SFT和RL的结合问题建模为一个领导者-跟随者博弈。SFT作为上层问题（领导者），RL作为下层问题（跟随者）。上层的SFT目标以最优的下层RL策略为条件，从而使SFT能够“元学习”如何指导RL的优化过程。
• 增强模型架构 (Augmented Model Architecture)：为了实现双层优化，模型参数被分解为两个部分：基础模型参数 \($\theta\)$ 和低秩适应 (Low-Rank Adaptation, LoRA) 参数 \($w\)$。下层RL优化基础参数 \($\theta\)$，而上层SFT则优化LoRA参数 \($w\)$。
• 协作增益 (Cooperative Gain)：这是上层优化目标的核心部分，定义为联合SFT-RL训练相对于单独RL训练的性能优势。通过在上层优化中显式地最大化这一增益，BRIDGE确保了SFT的指导对RL总是有益的，从而保证了协作的有效性。

相关工作

当前，提升大语言模型推理能力的主流方法包括监督微调 (Supervised Fine-Tuning, SFT) 和基于规则的强化学习 (Reinforcement Learning, RL)。SFT通过模仿专家数据快速学习推理模式，但泛化能力较差；RL通过试错探索获得更高性能，但训练效率低下。

实践中，最常见的做法是“冷启动” (Cold-Start) 的两阶段训练：先用SFT进行预热，再用RL进行微调。这种方法的关键瓶颈在于阶段解耦：

1. 灾难性遗忘 (Catastrophic forgetting)：切换到RL阶段后，模型会迅速忘记SFT阶段学到的知识。
2. 低效探索 (Inefficient exploration)：SFT的初始引导作用有限，在RL阶段模型仍可能陷入局部最优，无法解决难题。

本文旨在解决上述问题，设计一个统一的训练框架，让SFT和RL能够真正地协同作用，实现\(1+1>2\)的效果，并保证其性能优于单独使用RL。

本文方法

本文提出了BRIDGE，一个基于双层优化的协作式元学习框架，以实现SFT和RL的深度融合。

方法架构

BRIDGE采用了一个增强的模型架构，将模型参数分为两部分：

• 基础模型参数 \($\theta\)$：由下层的RL目标进行优化。
• LoRA模块参数 \($w\)$：由上层的SFT目标进行优化。

这种参数分离是实现双层优化的关键，使得两个目标可以在训练中共同适应，而不是相互覆盖。

双层优化公式

该框架被形式化为一个双层优化问题，其中SFT为上层问题，RL为下层问题：

\[\begin{align*} \max_{w} \quad & J_{\mathrm{SFT}}(w, \theta^*(w)) \\ \text{s.t.} \quad & \theta^*(w) = \arg\max_{\theta} J_{\mathrm{RL}}(\theta, w) \end{align*}\]

• 下层问题 (Follower)：在给定LoRA参数 \($w\)$ 的情况下，通过最大化RL目标 \($J\_{\mathrm{RL}}\)$ 来求解最优的基础模型参数 \($\theta^\*(w)\)$。
• 上层问题 (Leader)：寻找最优的LoRA参数 \($w\)$，使得经过下层RL优化后的模型 \($\theta^\*(w)\)$ 在SFT任务上的表现 \($J\_{\mathrm{SFT}}\)$ 最好。

这个结构实现了双向信息流：SFT（上层）能够“预见”RL（下层）的优化结果，从而提供更有针对性的指导。

学习算法与创新点

由于直接求解双层优化问题涉及复杂的二阶导数，计算成本高昂，本文采用了一种基于罚函数 (penalty-based) 的一阶松弛方法来近似求解。

1. 创新点一：下层更新 - 课程加权的梯度融合 对基础参数 \($\theta\)$ 的更新规则是SFT和RL梯度的加权和：

\[\theta^{k+1} = \theta^{k} + \alpha\left[(1-\lambda)\nabla_{\theta}J_{\mathrm{SFT}}(\theta,w) + \lambda\nabla_{\theta}J_{\mathrm{RL}}(\theta,w)\right]\]

其中，\($\lambda\)$ 是一个从0到1动态变化的权重。训练初期，模型主要通过模仿SFT数据来学习；随着模型能力增强，RL的权重逐渐增加，使模型更多地通过探索来学习。这种设计形成了一种自适应的课程学习 (curriculum learning) 机制。

2. 创新点二：上层更新 - 显式最大化协作增益 对LoRA参数 \($w\)$ 的更新旨在最大化一个复合目标，其核心是协作增益：

\[\underbrace{J_{\mathrm{RL}}(\theta,w) - J_{\mathrm{RL}}(\hat{\theta},w)}_{\text{协作增益}}\]

其中，\($\theta\)$ 是通过SFT和RL联合优化的参数，而 \($\hat{\theta}\) 则是仅通过RL优化的参数。这个增益项衡量了“SFT-RL联合训练”比“纯RL训练”带来的性能提升。通过最大化这个增益，上层SFT学会了如何提供对RL最有帮助的指导，从而在理论上保证了合作的效果优于单独的RL。

实验结论

本文在三个大语言模型（Qwen2.5-3B, Llama-3.2-3B, Qwen2-8B）和五个数学推理基准上进行了广泛实验。

核心发现

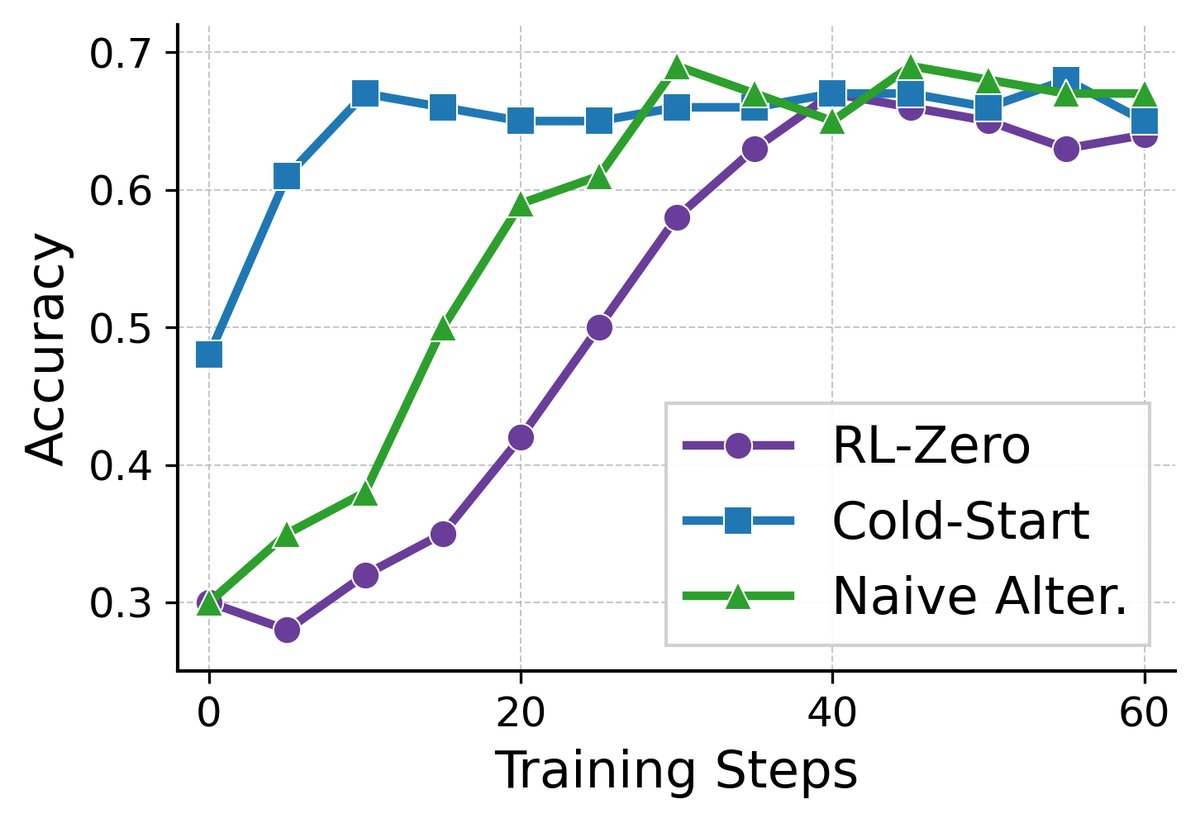
• 性能全面超越：在所有模型和数据集上，BRIDGE的性能均一致且显著地优于所有基线方法，包括SFT、RL-zero（从头开始RL）、Cold-start（两阶段）以及一个简单的交替训练基线。例如，在Qwen2.5-3B上，相比Cold-start，BRIDGE在多个挑战性数据集上取得了11.8%的平均性能提升。

方法	MATH500	Minerva Math	OlympiadBench	AIME24	AMC23	平均值
Base	32.4	11.8	7.9	0.0	20.0	14.4
SFT	53.4	18.8	21.5	3.3	42.5	27.9
RL-zero	64.4	26.5	27.0	3.3	40.0	32.2
Cold-start	66.0	24.3	26.8	9.0	35.0	32.2
Naive Alter.	65.2	25.3	27.1	6.7	42.5	33.4 (+3.7)
BRIDGE	66.2	23.9	28.9	13.3	47.5	36.0 (+11.8)

• 更强的泛化能力：BRIDGE在更困难的竞赛级数学推理任务（如OlympiadBench, AIME24）上表现出尤其优越的泛化能力，而基线方法在这些任务上性能提升有限甚至下降。

• 更高的训练效率：训练动态分析显示，Cold-start方法在RL阶段初期存在一个性能“先降后升”的模式，表明模型正在遗忘SFT知识，导致效率低下。相比之下，BRIDGE通过持续的SFT指导，实现了奖励的快速稳定增长，避免了灾难性遗忘。

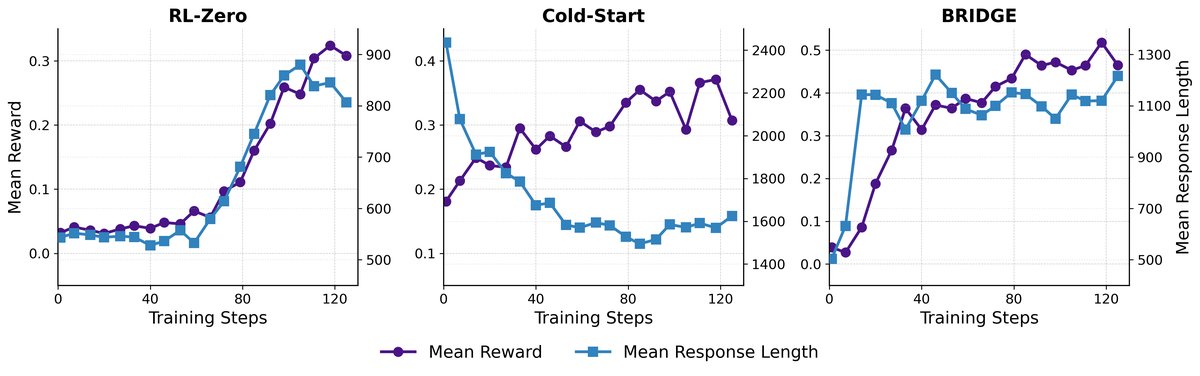
• 更优的成本效益：与需要近两倍训练时间的Cold-start方法相比，BRIDGE在取得更高性能的同时，节省了14%-44%的训练时间，展示了其在实际部署中的成本优势。

指标	Qwen 2.5-3B			Qwen 3-8B-Base
	RL-zero	Cold-start	BRIDGE	RL-zero	Cold-start	BRIDGE
时间 (小时)	6.1	12.3	6.9	38.5	39.1	33.5
显存 (GB)	52.2	45.9	59.3	50.7	60.8	67.4
准确率 (%)	32.2	32.2	36.4	42.9	45.5	49.9

总结

实验结果有力地证明了BRIDGE框架的有效性。通过将SFT和RL的结合建模为双层优化问题，BRIDGE不仅解决了传统两阶段方法的内在缺陷，还在性能和效率上实现了新的平衡，为训练强大的推理模型提供了一个更优越的范式。