Bi-LoRA: Efficient Sharpness-Aware Minimization for Fine-Tuning Large-Scale Models

TL;DR

本文提出了一种名为 Bi-LoRA 的高效微调框架，它通过引入一个独立的辅助 LoRA 模块来模拟锐度感知最小化（SAM）的对抗性扰动，从而在不增加额外计算成本（仅需一次反向传播）的情况下，有效提升大模型微调的泛化能力。

关键定义

本文沿用了 Sharpness-Aware Minimization (SAM) 和 Low-Rank Adaptation (LoRA) 的已有定义，并基于此提出了核心方法：

  1. LoRA-SAM：将 SAM 直接应用于 LoRA 参数的一种直接组合。其优化目标是最小化在 LoRA 参数 $(B, A)$ 的一个邻域内最差的损失。本文指出，这种方法将锐度优化限制在一个由 LoRA 参数自身定义的“受限子空间”内，从而限制了其泛化效果。

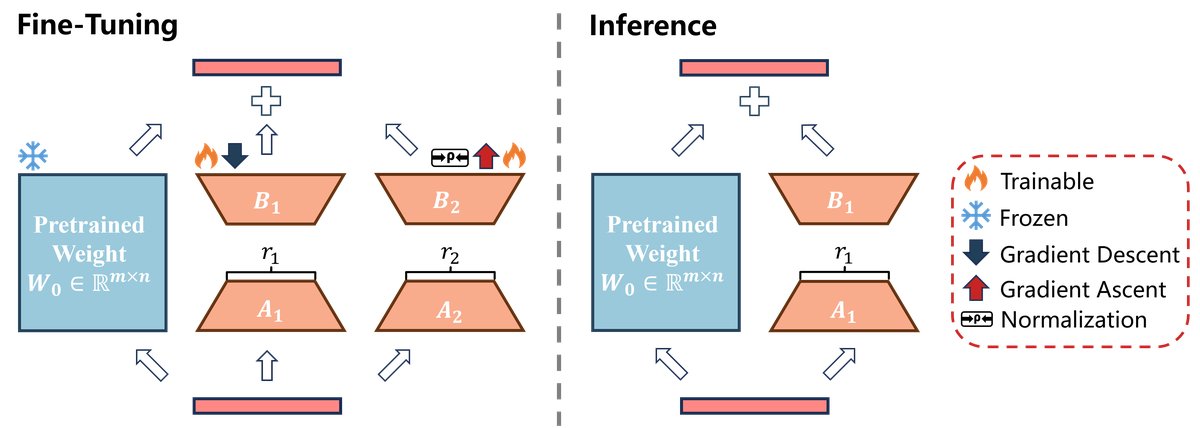
  2. Bi-LoRA (Bi-directional Low-Rank Adaptation, 双向低秩自适应)：本文提出的核心方法。它采用双模块架构，包含两个并行的 LoRA 模块：

    • 主 LoRA 模块 ($B_1A_1$)：通过标准的梯度下降进行优化，负责学习特定于任务的 адаптация。
    • 辅助 LoRA 模块 ($B_2A_2$)：通过梯度上升进行优化，专门用于模拟 SAM 中的对抗性权重扰动，以探索损失平坦度。

    这种设计解耦了任务适应和锐度优化的过程，使得模型可以在单次前向和后向传播中同时完成两个方向的优化，从而在保持高效率的同时获得更好的泛化性能。

相关工作

当前，通过预训练再微调的范式在机器学习领域已成为标准。然而，随着模型规模的急剧增大，在有限数据上进行微调时，模型极易出现过拟合，损害泛化能力。

一个有前景的方向是寻找损失函数上的“平坦最小值” (flat minima)，因为这通常与更好的泛化性能相关。Sharpness-Aware Minimization (SAM) 正是为此设计的优化器，它通过求解一个最小-最大（min-max）问题来寻找平坦区域，在小规模训练中取得了显著成功。但 SAM 的主要瓶颈在于其高昂的计算成本：它需要在每个训练步骤中进行两次前向和后向传播，这对于微调大型模型而言几乎是不可行的。

为了解决大模型微调的效率问题，以 Low-Rank Adaptation (LoRA) 为代表的参数高效微调（PEFT）方法被广泛应用。LoRA 通过引入少量可训练的低秩矩阵来近似权重更新，极大地降低了内存和计算开销。

本文旨在解决的问题是：如何将 SAM 的泛化优势高效地应用于 LoRA 微调？直接的结合（即 LoRA-SAM）存在一个根本性的不匹配：对抗性扰动被限制在 LoRA 参数定义的低维子空间内，无法有效优化整个参数空间的锐度。本文提出的 Bi-LoRA 正是为了解决 LoRA-SAM 这种“子空间耦合”问题，旨在实现高效且更有效的锐度感知优化。

本文方法

本文的核心方法 Bi-LoRA 通过引入双 LoRA 模块，解耦了任务适应与锐度优化，从而实现了高效且强大的泛化能力提升。

Bi-LoRA框架概览

图1: Bi-LoRA 框架概览。微调时（左），主 LoRA 模块 ($B\_1A\_1$) 通过梯度下降进行任务适应，辅助 LoRA 模块 ($B\_2A\_2$) 通过梯度上升注入对抗性扰动。推理时（右），仅保留主模块，辅助模块被丢弃。

LoRA-SAM 的问题：受限子空间

在将 SAM 应用于 LoRA 时，一个自然的想法是直接对 LoRA 参数 $B$ 和 $A$ 施加扰动。这种方法被称为 LoRA-SAM，其优化目标为：

\[\min_{B,A} \max_{\ \mid \left(\mathbf{\epsilon}_{B},\mathbf{\epsilon}_{A}\right)\ \mid \leq\rho} \mathcal{L}\left({W}_{0}+({B}+\mathbf{\epsilon}_{B})({A}+\mathbf{\epsilon}_{A})\right)\]

其中 $(\epsilon_B, \epsilon_A)$ 是对 LoRA 矩阵的对抗性扰动。经过分析，施加在整个权重矩阵上的有效扰动 $\epsilon_W$ 可以近似为：

\[\epsilon_W \approx c\left[BB^{\top}(\nabla_W\mathcal{L})+(\nabla_W\mathcal{L}){A}^{\top}A\right]\]

Proposition 3.1 指出，这种扰动被严格限制在由主 LoRA 矩阵定义的列空间 $\text{Col}(B)$ 和行空间 $\text{Row}(A)$ 内。这意味着 LoRA-SAM 仅仅在 LoRA 参数的低维子空间内寻找平坦区域，而忽略了在更广阔的全参数空间中的锐度，这限制了其提升泛化能力的效果。如下图所示，LoRA-SAM 虽然在 LoRA 参数空间（图a）中实现了最佳平坦度，但在全参数空间（图b）中，其损失仍然会随着扰动急剧上升。

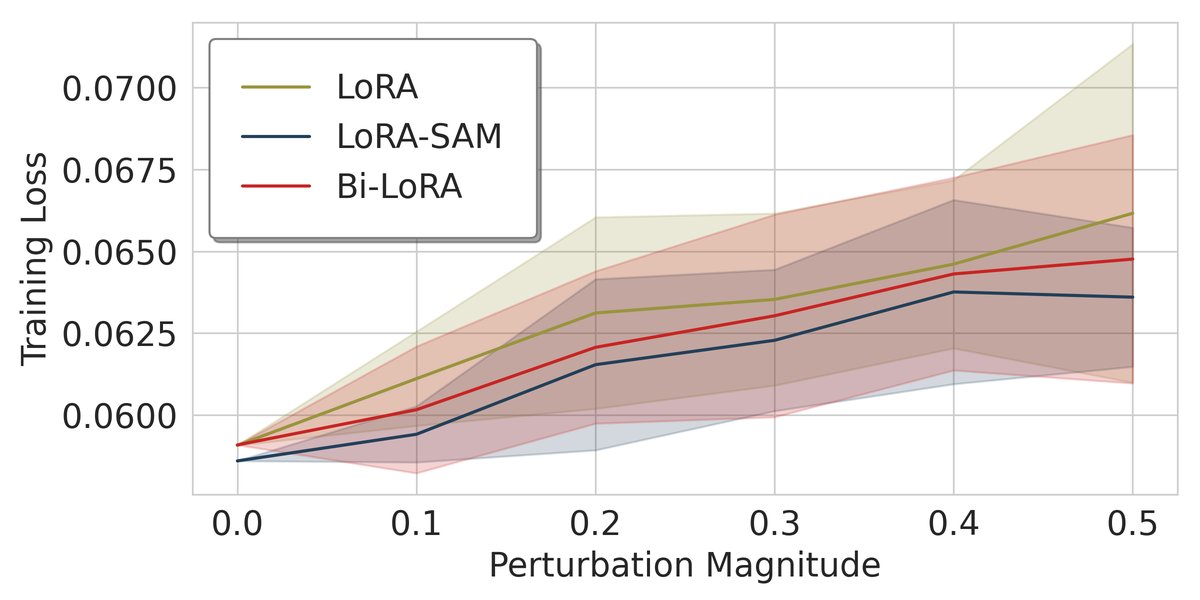损失景观可视化 (a) LoRA 参数空间

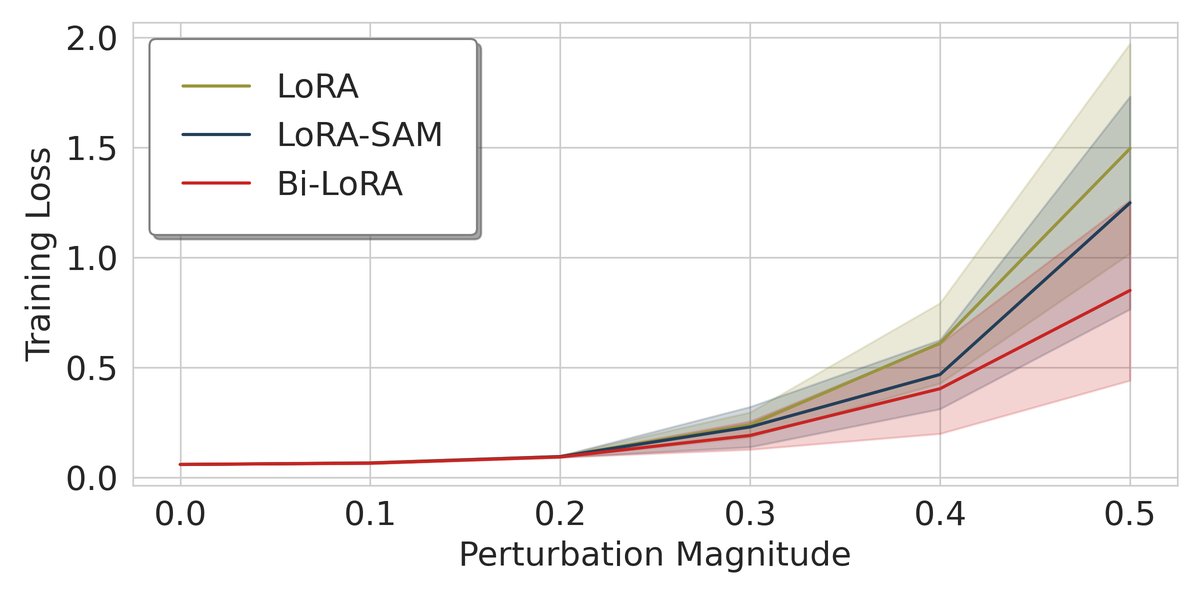损失景观可视化 (b) 全参数空间

图3: 损失景观可视化。与 LoRA 相比，Bi-LoRA 在全参数空间 (b) 中实现了显著更大的平坦度增益。

Bi-LoRA：双向低秩自适应

为了解决上述问题，Bi-LoRA 提出使用两个独立的 LoRA 模块来解耦优化与扰动：

\[W = W_0 + B_1A_1 + B_2A_2\]

其中，$B_1A_1$ 是主模块，负责任务微调；$B_2A_2$ 是辅助模块，负责模拟对抗性扰动。其优化目标变为：

\[\min_{B_1,A_1} \max_{\ \mid B_2A_2\ \mid _F\leq\rho} \mathcal{L}\left(W_0+B_1A_1+B_2A_2\right)\]

Proposition 4.1 指出，Bi-LoRA 的扰动空间由 $\text{Col}(B_2)$ 张成，这与主模块的优化空间 $\text{Col}(B_1)$ 是完全解耦的。这使得模型能够探索更广泛的参数空间以寻找平坦区域，从而获得更好的泛化能力。

创新点：高效的双向优化

Bi-LoRA 最大的创新之一是其高效的优化策略。由于优化和扰动由不同模块负责，它们可以在同一次反向传播中同时进行更新：

  1. 主模块 $(B_1, A_1)$：执行梯度下降，以最小化任务损失。
  2. 辅助模块 $(B_2, A_2)$：执行梯度上升，以最大化任务损失（即寻找最陡峭的上升方向）。

更新规则如下：

\[\left\{ \begin{aligned} B_1^{k+1} &= B_1^{k}-\eta_1(\nabla_W\mathcal{L}){A^{k\top}_1}, \quad A_1^{k+1}=A_1^{k}-\eta_1B_1^{k\top}(\nabla_W\mathcal{L}), \\ B_2^{k+1} &= B_2^{k}+\eta_2(\nabla_W\mathcal{L})A_2^{k\top}, \quad A_2^{k+1}=A_2^{k}+\eta_2B_2^{k\top}(\nabla_W\mathcal{L}), \end{aligned} \right.\]

这种“双向”更新机制避免了 SAM 所需的两次梯度计算，使得 Bi-LoRA 的训练速度几乎与标准 LoRA 相同，同时获得了 SAM 的泛化优势。

为保证扰动幅度受控，每次更新后，会对辅助模块的 Frobenius 范数进行裁剪，确保其总范数不超过预设的邻域半径 $\rho$。

算法伪代码 ``$$ Algorithm 1 Bi-LoRA

1: 输入: 初始权重 W_0, 学习率 η_1, η_2, 半径 ρ, LoRA层数 N 2: 输出: 推理用权重 W 3: 初始化 LoRA 模块 B_1^0, A_1^0, B_2^0, A_2^0; 4: k ← 0; 5: while 未收敛 do 6: 采样小批量数据 B; 7: 通过 Eq. (9) 对主模块进行梯度下降，对辅助模块进行梯度上升; 8: 通过 Eq. (10) 裁剪辅助模块; 9: k ← k + 1; 10: end while 11: 移除辅助 LoRA 模块 B_2^k, A_2^k; 12: return W^k = W_0 + B_1^k A_1^k $$``

推理

训练结束后，辅助模块 $(B_2A_2)$ 被完全丢弃，因为它仅在训练阶段用于引导主模块寻找平坦区域。最终用于推理的模型结构与标准 LoRA 完全相同 ($W = W_0 + B_1A_1$)，不引入任何额外的推理开销。

实验结论

本文通过在自然语言理解（NLU）、大型语言模型（LLM）和扩散模型等多种任务上的广泛实验，验证了 Bi-LoRA 的有效性和高效率。

关键实验结果：

  1. NLU 任务 (GLUE & SuperGLUE)：在使用 T5-base 模型的实验中，Bi-LoRA 在多个数据集上全面优于 LoRA 和 LoRA-SAM。特别是在数据量较小的 CoLA和MRPC 等任务上，性能提升更为显著，平均提升分别达到 1.36% 和 0.82%。相比之下，LoRA-SAM 收益甚微。
方法 成本 MNLI SST2 CoLA QNLI MRPC 平均
LoRA ×1 86.25 94.23 59.41 93.25 88.56 84.34
LoRA-SAM ×2 86.25 94.46 59.80 93.21 88.73 84.49
Bi-LoRA ×1 86.33 94.34 60.77 93.25 89.38 84.81
表1: T5-base 在 GLUE 子集上的结果
  1. 大型语言模型任务 (Llama 2/3.1)：在针对 Llama-7B/8B 的数学推理（GSM8K）、代码生成（HumanEval）、对话（MT-Bench）和指令跟随等任务中，Bi-LoRA 的优势更加明显。例如，在 GSM8K 和 HumanEval 上，Bi-LoRA 分别比 LoRA 提升了 2.11% 和 2.45%。在某些任务上，Bi-LoRA 甚至超越了全量微调（Full FT）的性能。
方法 成本 GSM8K (Llama 2) HumanEval (Llama 2) MT-Bench (Llama 2)
LoRA ×1 58.21 24.75 6.08
LoRA-SAM ×2 59.16 26.59 5.82
Bi-LoRA ×1 60.32 27.20 6.24
表3: Llama-7B/8B 在不同任务上的部分结果

  1. 扩散模型任务：在 SDXL 模型的 Dreambooth 微调任务中，Bi-LoRA 在提升个性化（CLIP I2T 相似度）和保留文本一致性（CLIP T2T 相似度）方面均优于 LoRA。

  2. 效率对比：Bi-LoRA 的训练时长几乎与标准 LoRA 持平（约为 LoRA 的 103%-115%），而 LoRA-SAM 则需要超过两倍（200%+）的时间。同时，Bi-LoRA 引入的内存开销极小。

方法 T5-base 时间 Llama 2-7B 时间 Llama 3.1-8B 时间
LoRA 0.27s (100%) 4.34s (100%) 9.49s (100%)
LoRA-SAM 0.55s (204%) 9.35s (215%) 19.55s (206%)
Bi-LoRA 0.31s (115%) 4.50s (104%) 9.75s (103%)
表7: 训练时间和内存成本对比
  1. 兼容性：Bi-LoRA 可以与其他 LoRA 变体（如 DoRA, PiSSA）无缝集成，并带来持续的性能提升，证明了其方法的正交性和通用性。

最终结论 实验结果有力地证明，Bi-LoRA 是一种高效且有效的微调技术。它通过解耦优化和扰动，成功地将 SAM 的泛化优势带到了大型模型的参数高效微调中，同时几乎不增加任何额外的训练时间成本，为在有限资源下提升大模型的泛化能力提供了新的SOTA解决方案。