BroRL: Scaling Reinforcement Learning via Broadened Exploration
-
ArXiv URL: http://arxiv.org/abs/2510.01180v1
-
作者: Fang Wu; Jian Hu; Jan Kautz; Ximing Lu; Pavlo Molchanov; Yejin Choi; Zaid Harchaoui; Yi Dong; Mingjie Liu; Shizhe Diao; 等11人
-
发布机构: NVIDIA; Stanford University; University of Washington
TL;DR
本文提出了一种名为 BroRL 的强化学习扩展范式,它通过显著增加每个样本的探索次数 (rollouts) 来拓宽探索范围,从而有效克服了传统按训练步数扩展方法遭遇的性能瓶颈,实现了持续且高效的模型性能提升。
关键定义
本文的核心论证建立在一个原创的理论分析框架之上,并沿用了一些强化学习领域的标准术语。以下是理解本文最关键的概念:
- 质量平衡方程 (Mass Balance Equation) 分析: 本文独创的理论分析方法,借鉴了物理学中分析质量传递的思想。该方法用于精确刻画单步强化学习更新过程中,正确和不正确Token的概率质量总和的变化率,从而揭示了不同因素对策略优化的影响。
- 正确Token的概率质量 (\(Q_pos\)): 指模型对一个给定问题所有可能正确答案(Token)所分配的概率之和。\(Q_pos\) 的增加直接关联到模型解决问题成功率(如 \(pass@k\) 指标)的提升。
- 概率二阶矩 (Second Moments of Probability): 衡量概率分布集中度的指标,如 \($A\_2, B\_2, U\_{\mathrm{pos},2}, U\_{\mathrm{neg},2}\)$。它们分别代表“已采样正确Token”、“已采样错误Token”、“未采样正确Token”和“未采样错误Token”的概率平方和。这些值在本文的理论公式中用以量化不同Token集合对整体概率质量变化的影响。
- 批次情绪 (Batch “Mood” \(S_R\)): 定义为 \($S\_R = R\_c P\_{\mathrm{pos}} + R\_w P\_{\mathrm{neg}}\)$,表示一个批次内所有已采样Token的奖励加权概率总和。\($S\_R > 0\)$ 表示这是一个“奖励为正”的批次,反之亦然。该值决定了未采样Token的概率质量将如何变化。
相关工作
当前,利用带有可验证奖励的强化学习 (Reinforcement Learning with Verifiable Rewards, RLVR) 来提升大语言模型复杂推理能力是一种前沿方法。近期代表性的工作 ProRL 通过增加训练步数来扩展强化学习,在初期取得了显著效果。
然而,这种方法的瓶颈在于,当训练达到数千步后,模型性能会进入平台期,继续增加计算投入以进行更多步数的训练,其回报会急剧下降,甚至出现性能衰退。
本文旨在解决这一核心问题:当通过增加训练步数来扩展强化学习的方法达到饱和时,如何才能继续有效提升模型性能?
本文方法
理论分析:质量平衡方程
本文的理论核心是基于一个简化的单步 RLVR 更新模型,通过质量平衡方程来分析正确Token的总概率质量 \($Q\_{\mathrm{pos}}\)$ 的变化 \($\Delta Q\_{\mathrm{pos}}\)$。
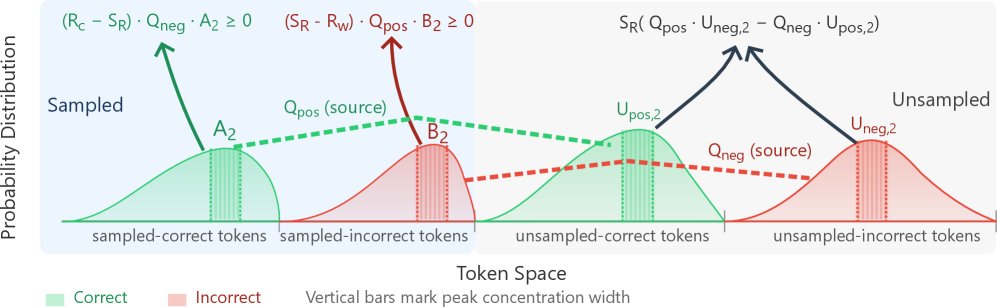
分析得出的核心方程为:
\[\Delta Q_{\mathrm{pos}}=\frac{\eta}{N}\Big[(R_{c}-S_{R})Q_{\mathrm{neg}}A_{2}\;+\;(S_{R}-R_{w})Q_{\mathrm{pos}}B_{2}\;+\;S_{R}\big(Q_{\mathrm{pos}}U_{\mathrm{neg},2}-Q_{\mathrm{neg}}U_{\mathrm{pos},2}\big)\Big]\]这个方程将 \($\Delta Q\_{\mathrm{pos}}\)$ 分解为三个部分,揭示了RL更新的内部动态:
- 已采样-正确项:\($(R\_c - S\_R)Q\_{\mathrm{neg}}A\_2\)$。此项源于对采样到的正确Token进行奖励。它总是非负的,意味着奖励正确的Token总会从错误Token的概率池 (\($Q\_{\mathrm{neg}}\)$) 中“抽取”概率,从而增加正确Token的概率质量。
- 已采样-错误项:\($(S\_R - R\_w)Q\_{\mathrm{pos}}B\_2\)$。此项源于对采样到的错误Token进行惩罚。它也总是非负的,因为降低错误Token的概率会释放出概率质量,并按比例分配给正确Token的概率池 (\($Q\_{\mathrm{pos}}\)$)。
- 未采样-耦合项:\($S\_R(Q\_{\mathrm{pos}}U\_{\mathrm{neg},2} - Q\_{\mathrm{neg}}U\_{\mathrm{pos},2})\)$。此项来自未被采样的Token,其正负符号不确定,是导致训练不稳定的关键。它的影响取决于批次的“情绪”\($S\_R\)$ 以及未采样区域中正确与错误Token的概率集中度。例如,在一个奖励为正的批次 (\($S\_R > 0\)$) 中,如果未采样的错误Token比正确Token更集中 (\($U\_{\mathrm{neg},2} > U\_{\mathrm{pos},2}\)$),该项为正;反之则为负,可能抵消前两项带来的收益。
创新点
本文方法 BroRL (Broad Reinforcement Learning) 的本质创新在于,它识别并解决了强化学习过程中的一个关键不稳定性来源——“未采样-耦合项”。
与以往方法的本质区别:传统方法如 ProRL 致力于通过增加训练 步数 来扩展RL,而 BroRL 则开辟了一个新的扩展维度:增加每个训练样本的 探索次数(rollouts per example, \($N\)$)。
核心优点:
- 稳定化学习信号:理论分析明确指出,随着探索次数 \($N\)$ 的增大,未采样Token的概率二阶矩 \($U\_{\mathrm{pos},2}\)$ 和 \($U\_{\mathrm{neg},2}\)$ 会指数级衰减 (\($\mathbb{E}[U\_2(p)] = p^2(1-p)^N\)$ )。这意味着,通过采用极大的 \($N\)$(如512),不稳定的“未采样-耦合项”的影响可以被有效抑制。这使得整体的策略更新 \($\Delta Q\_{\mathrm{pos}}\)$ 趋向于稳定为正,确保了学习过程的持续改进。
- 克服知识萎缩:大的 \($N\)$ 保证了对解空间的充分探索,使得模型在学习新知识时,不会忘记或损害已有的正确知识(即消除了知识萎缩 phenomenon of knowledge shrinkage)。
- 计算与数据效率:在实践中,BroRL 在相同的训练时间内,通过大 \($N\)$ 的设计实现了更高的计算效率。它在算法层面减少了动态采样过程中的样本丢弃率,并在硬件层面将计算从内存密集型转化为计算密集型,从而将训练吞吐量提升了近一倍。
BroRL 建立在 ProRLv2 框架之上,采用 PPO 算法,但将每个prompt的rollout数量 \($N\)$ 从16大幅提升至512。为适应增大的有效批次大小,学习率也根据批次大小的平方根进行了相应调整,以维持训练稳定。
实验结论
仿真实验
为验证理论分析的正确性,本文首先构建了一个Token级别的模拟器。实验设置了一个包含128,000个Token的词汇表,其中10,000个为正确Token。
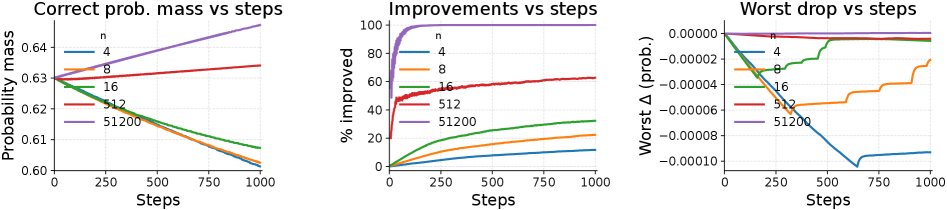
仿真结果与理论预测高度一致:
- 更快的性能提升:更大的探索次数 \($N\)$ 使得正确Token的总概率质量 \($Q\_{\mathrm{pos}}\)$ 增长更快、更稳定。
- 消除知识萎缩:当 \($N\)$ 较小时,部分正确Token的概率在训练中会下降(即知识萎缩)。而当 \($N\)$ 足够大时(如512),这种负面影响完全消失,所有正确Token的概率都能得到提升。
这证实了通过增加 \($N\)$ 来抑制未采样项负面影响的理论是有效的。
大模型实证研究
本文在真实的大语言模型上进行了实验。实验在一个已经经过3000步ProRL训练并已达到性能饱和的1.5B模型上继续进行。
Pass@1 成功率分析: 在同等计算成本下,对比了继续使用ProRL(小 \($N=16\)$)和切换到BroRL(大 \($N=512\)$)的训练效果。结果呈现三种典型轨迹:
- BroRL 表现持续优于 ProRL。
- ProRL 性能下降,而 BroRL 持续改进。
- 两者均无明显提升(表明对于某些极难问题,\($N=512\)$ 可能仍不足够)。 大多数任务属于前两种情况,从统计学上看,配对t检验显示 BroRL 相比 ProRL 具有显著的优势(\($p=6.5\times 10^{-7}\)$),证明了其更强的学习动态和泛化能力。
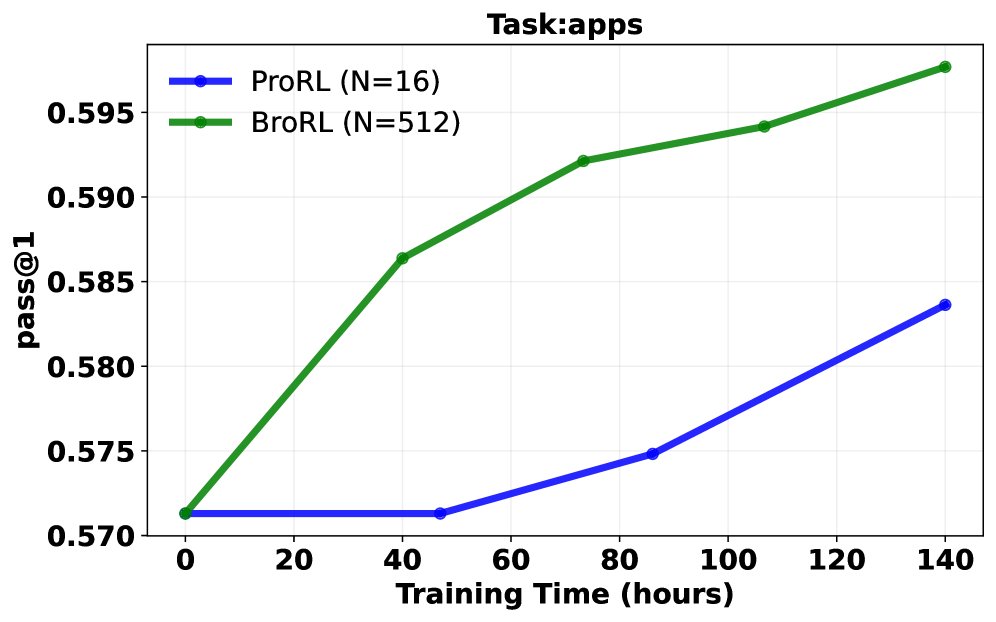
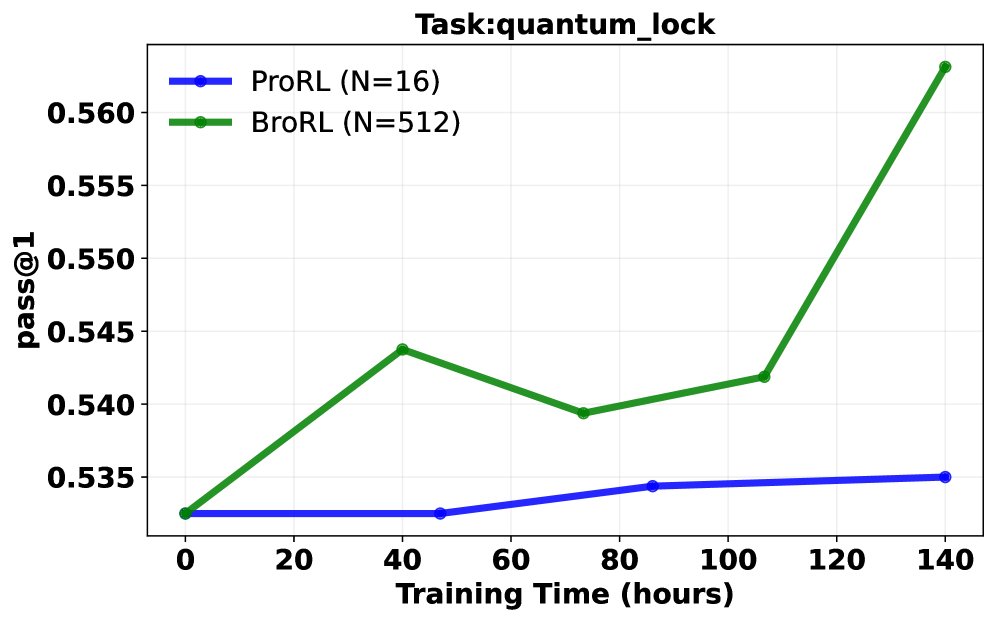
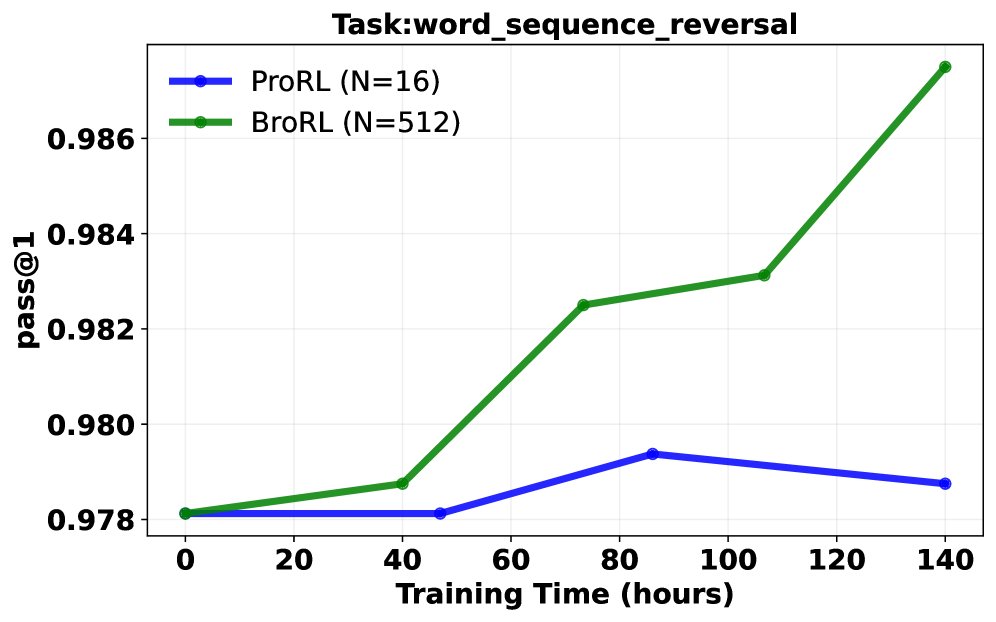
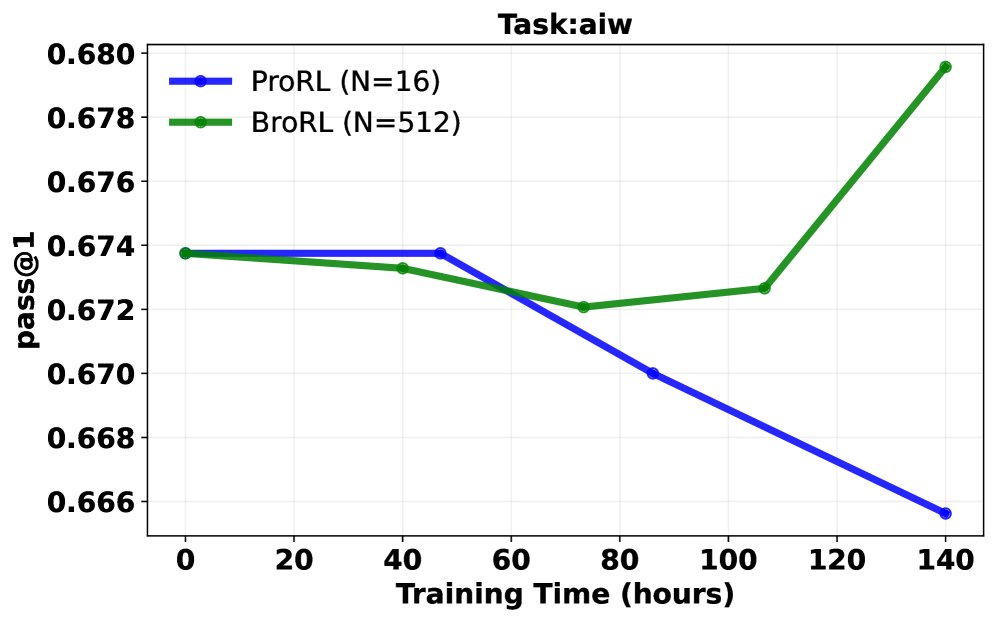
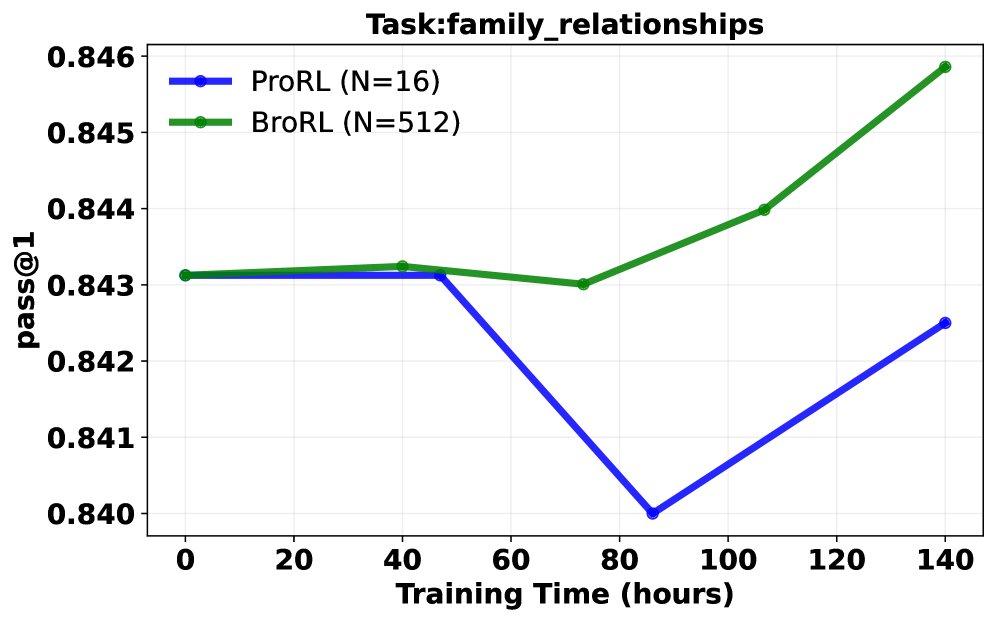
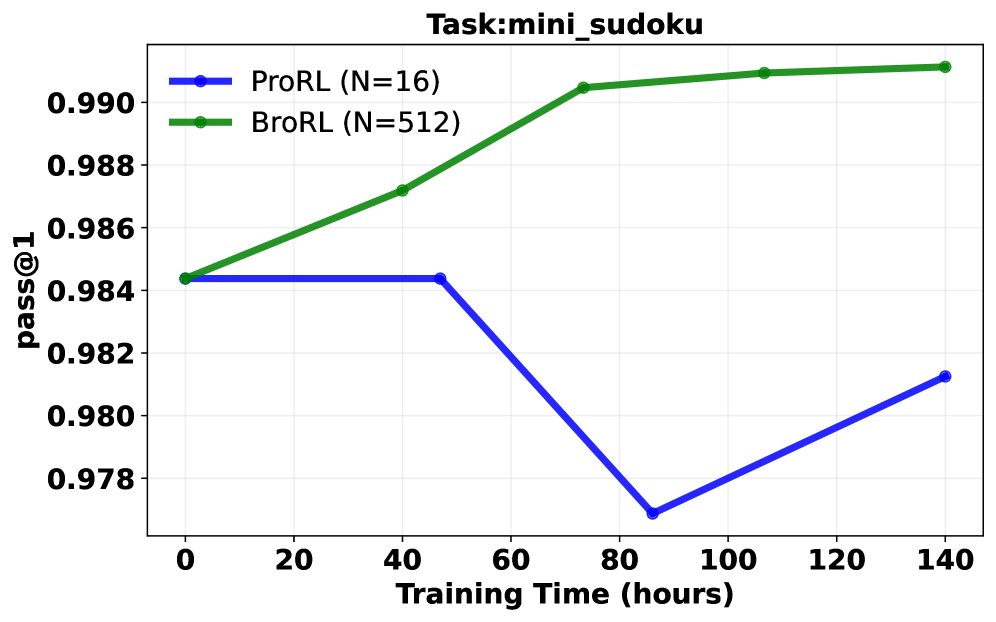
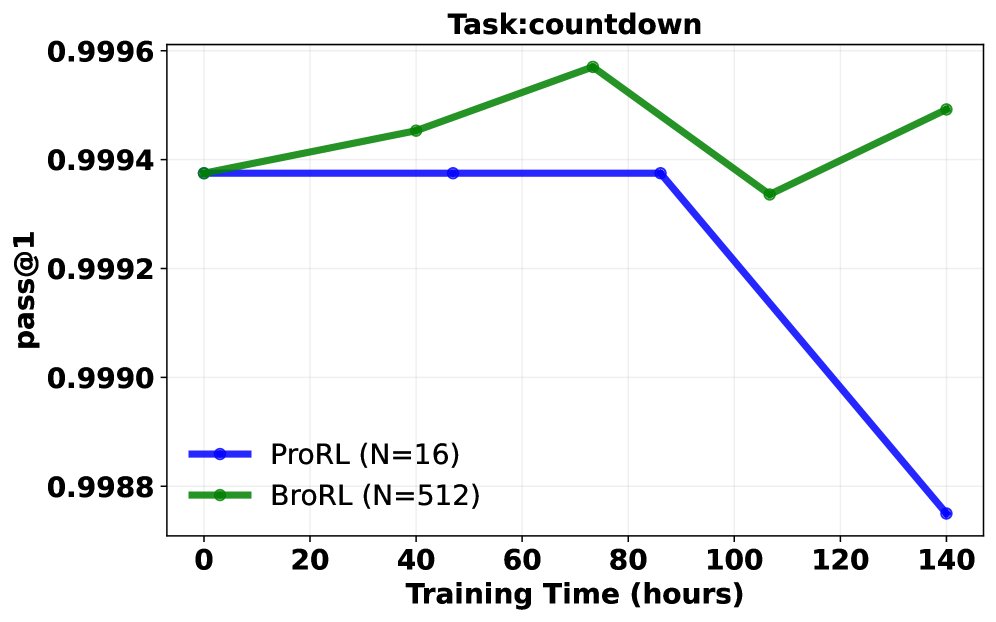
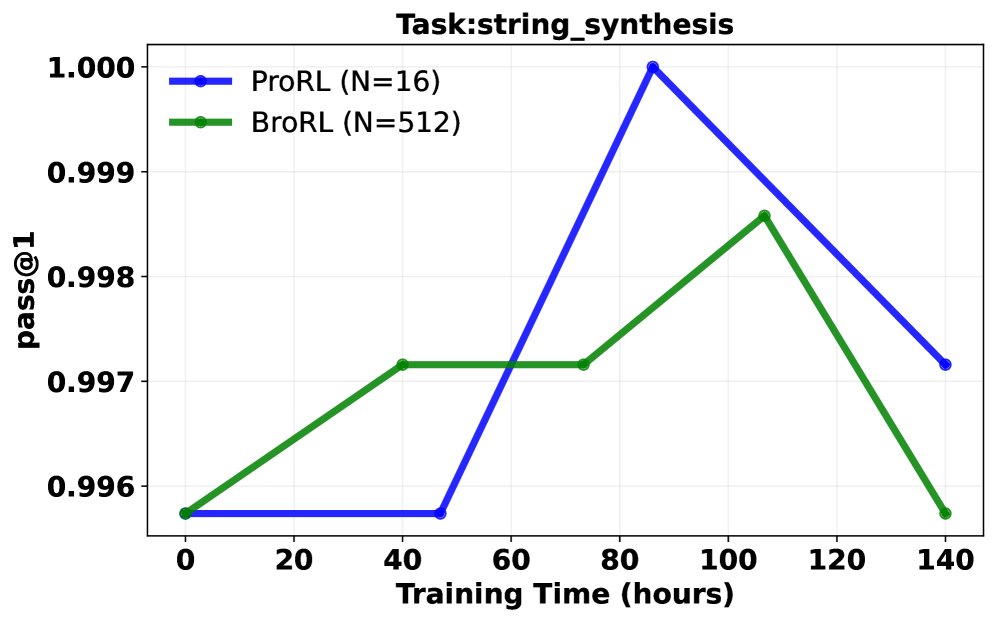
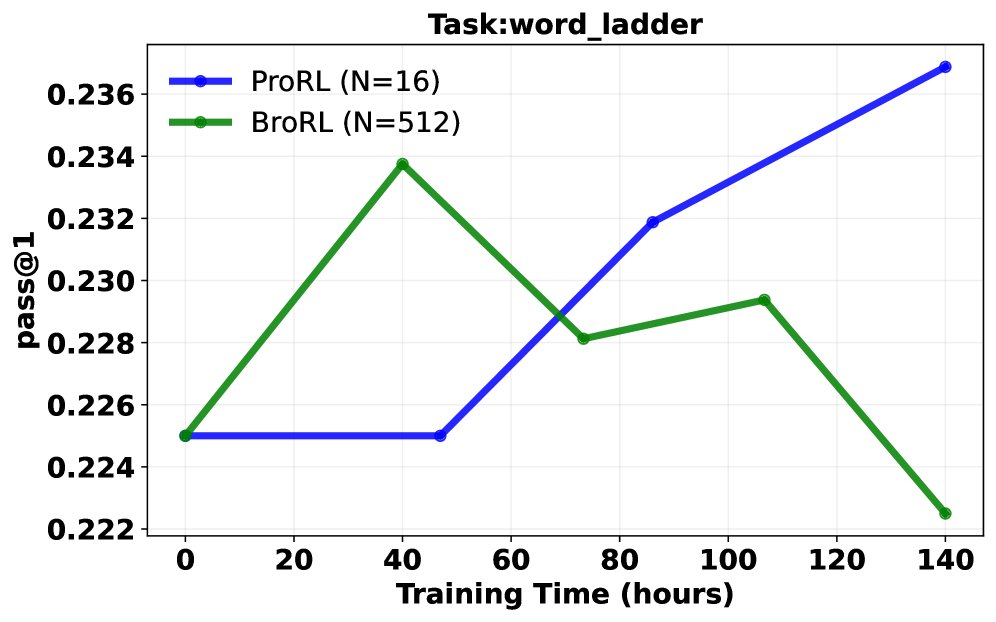
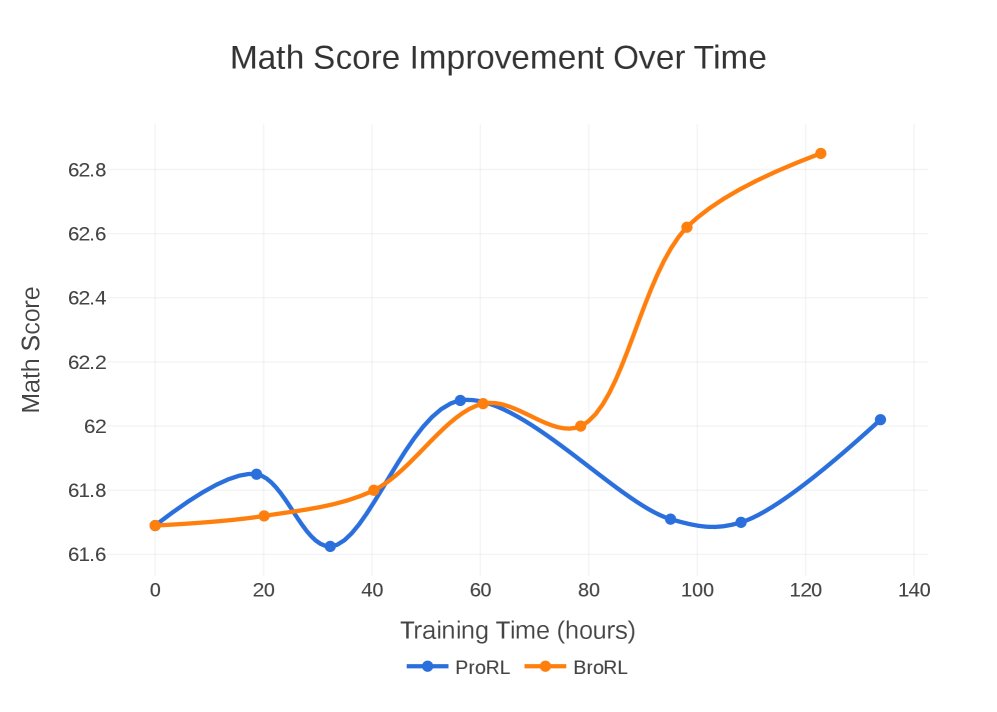
突破性能瓶颈: 实验证明,对于已饱和的模型,ProRL的“步数扩展”策略很快失效并导致性能下降。相反,BroRL的“探索扩展”策略则能成功“复活”模型,使其性能在数学、代码和推理等多个基准上持续稳健增长,并最终达到新的SOTA水平。
| 方法 | 训练时间 (小时) | 已处理样本数 (M) | Math Score | Code Score | Reasoning Score |
|---|---|---|---|---|---|
| ProRLv2 (基线) | 0 | 0 | 61.94 | 52.68 | 61.85 |
| ProRL (续训练) | 133.8 | 104 | 62.02 | 52.74 | 61.45 |
| BroRL (续训练) | 140.7 | 530 | 63.03 | 54.20 | 63.09 |
效率与性能对比。BroRL在更短的时间内取得了更高的分数,而ProRL停滞并退化。
总结
实验结果有力地证明,BroRL不仅在理论上更稳健,在实践中也更有效。它揭示了RLVR的性能极限有时并非RL方法本身的瓶颈,而是由于算法设计(如探索不足)造成的人为限制。通过将计算资源从“训练更深”转向“探索更广”,BroRL为扩展强化学习提供了一条全新且高效的途径。