Connecting Jensen-Shannon and Kullback-Leibler Divergences: A New Bound for Representation Learning

ArXiv URL: http://arxiv.org/abs/2510.20644v1
作者: Polina Golland
发布机构: Harvard; Inria; MIT

TL;DR

本文推导出了一个连接Kullback-Leibler散度（KLD）和Jensen-Shannon散度（JSD）的新的、紧致的下界，从而在理论上证明了最大化基于JSD的判别器目标函数等同于最大化互信息（MI）的一个可靠下界，为表示学习中广泛使用的判别式方法提供了坚实的理论基础。

关键定义

本文的核心是建立JSD和KLD之间的数学联系。关键定义如下：

互信息 (Mutual Information, MI)：衡量两个随机变量 $U$ 和 $V$ 之间统计依赖性的基本指标。它被定义为联合分布 $p_{UV}$ 与边缘分布乘积 $p_U \otimes p_V$ 之间的KL散度。
\[{\rm I}\left[U;V\right] \doteq {{\rm D_{KL}}}[{p_{UV}}\; \mid \mid \;{p_{U}\otimes p_{V}}]\]
基于JSD的信息量 (${\rm I_{JS}}$)：本文提出的一个概念，指代联合分布 $p_{UV}$ 和边缘分布乘积 $p_U \otimes p_V$ 之间的Jensen-Shannon散度。许多现有工作凭经验优化此目标，本文为其提供了理论依据。
\[{\rm I_{JS}}\left[U;V\right] \doteq {{\rm D_{JS}}}[{p_{UV}}\; \mid \mid \;{p_{U}\otimes p_{V}}]\]
KLD下界函数 ($\Xi(\cdot)$)：本文最重要的理论贡献，一个将JSD值映射到KLD紧致下界的单调递增函数。该函数没有简单的封闭解析式，但其反函数 $\Xi^{-1}$ 有明确定义，并通过特定伯努利分布的JSD值计算得出。它的存在意味着最大化JSD必然会最大化KLD的一个下界。
\[\Xi\left({{\rm D_{JS}}}[{p}\; \mid \mid \;{q}]\right) \leq {{\rm D_{KL}}}[{p}\; \mid \mid \;{q}]\]
$f$-散度的联合范围 (Joint range of $f$-divergences)：一个理论工具，指对于一对$f$-散度 $(D_f, D_g)$，所有可能的散度值对 $(D_f(p\ \mid q), D_g(p\ \mid q))$ 构成的集合。本文利用KLD和JSD的联合范围，特别是其下边界，来推导出 KLD 关于 JSD 的最紧下界。一个关键性质是，该范围仅通过分析二元分布（伯努利分布）即可完全刻画。

本文方法

本文的核心思想是构建一个从易于优化的判别器损失到互信息下界的完整数学链条。该方法可分为两个关键步骤，最终将它们连接起来。

创新点1：KLD关于JSD的新下界

本文的第一个核心贡献是推导出了KLD关于JSD的一个新的、最优的（即最紧的）下界。

该下界由一个单调递增函数 $\Xi(\cdot)$ 给出：

\[\Xi\left({{\rm D_{JS}}}[{p}\; \mid \mid \;{q}]\right) \leq {{\rm D_{KL}}}[{p}\; \mid \mid \;{q}]\]

这个不等式表明，任何能增大JSD的操作，也必然能增大KLD的一个保证的下界。

该下界的推导基于对 $f$-散度联合范围的分析。作者发现，要确定任意分布 $p, q$ 的 $(D_{\rm JS}, D_{\rm KL})$ 值对的集合范围，只需研究最简单的伯努利分布对即可。这个范围的下边界曲线定义了最优下界函数 $\Xi$。具体来说，这条边界是在一个分布是确定性的（例如，概率为1），而另一个分布的参数在变化时形成的。

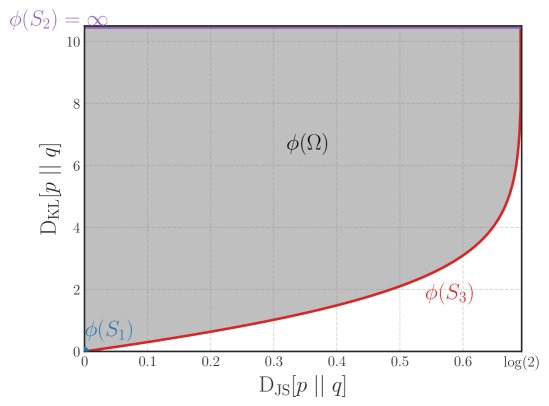
$左：两个伯努利分布的参数空间。右：映射 \phi 的图像（灰色区域），显示了JS散度和KL散度的联合范围。红色曲线是本文提出的新下界。$

尽管 $\Xi$ 没有封闭形式的表达式，但其反函数 $\Xi^{-1}$ 可以被定义，并且作者提供了一个使用Logit函数 $\mathbb{L}(x)$ 的紧密可微近似：

\[\Xi(x)\approx 1.15\*\mathbb{L}\left(.5\left(\frac{x}{\log 2}+1.0\right)\right)\]

将此结果应用于互信息场景（即 $p=p_{UV}, q=p_U \otimes p_V$），直接得到：

\[\Xi\left({\rm I_{JS}}\left[U;V\right]\right) \leq {\rm I}\left[U;V\right]\]

创新点2：连接JSD与判别器交叉熵损失

本文的第二个步骤是将理论上的 $I_{\rm JS}$ 与实践中可操作的判别器损失联系起来。这借鉴了GANs中的思想，但为MI估计提供了清晰的视角。

考虑一个判别器，其任务是区分来自联合分布 $p_{UV}$ 的“真实”样本对（标签为1）和来自边缘分布乘积 $p_U \otimes p_V$ 的“虚假”样本对（标签为0）。如果使用标准的二元交叉熵（Cross-Entropy, CE）损失 $\mathcal{L}_{\rm CE}$ 来训练这个判别器，那么可以证明JSD满足以下不等式：

\[\log 2 - \mathcal{L}_{\rm CE} \leq {\rm I_{JS}}\left[U;V\right]\]

这个不等式表明，最小化判别器的交叉熵损失等价于最大化 $I_{\rm JS}$ 的一个下界。当判别器达到最优时，该下界是紧的。

最终的MI变分下界

将以上两个结果串联起来，本文得到了最终的、端到端的互信息变分下界 $I_{CE}(\theta)$：

\[I_{CE}(\theta)\doteq\Xi\left(\log 2-{\mathcal{L}}_{CE}\left(\theta\right)\right)\ \leq\ \Xi\left({\rm I_{JS}}\left[U;V\right]\right)\ \leq\ {\rm I}\left[U;V\right]\]

这个链式不等式是本文的核心理论成果。它清晰地表明：最小化一个旨在区分联合样本与边缘样本的分类器的交叉熵损失，会驱动一个互信息的紧致下界 $I_{CE}(\theta)$ 的最大化。

这为Deep InfoMax等方法的成功提供了坚实的理论解释，并提出了一个全新的、有理论依据的MI变分下界估计器 $I_{CE}$。此外，训练好的判别器还可以通过Logit变换直接用于估计MI值本身，这与GAN-DIME等方法一致。

实验结论

本文通过一系列实验，从理论和实践两方面验证了所提方法的有效性。

下界的紧致性验证

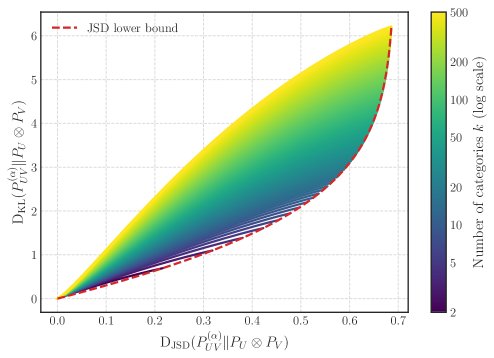
在离散分布设定下，MI和$I_{\rm JS}$都可以被精确计算。作者构建了一系列参数化的离散联合分布，其依赖程度从完全独立（$\alpha=0$）到完全相关（$\alpha=1$）平滑过渡。实验结果显示，对于不同维度 $k$ 的情况，计算出的真实MI值与本文提出的下界 $\Xi(I_{\rm JS})$ 构成的曲线非常接近。这有力地证明了该理论下界在实践中是紧致的（tight），即存在真实分布使得MI值能够接近甚至达到这个界限。

$对于一个具有已知MI和JSD的参数化离散联合分布族，互信息与其基于JSD的下界 \Xi(I_JS) 的关系。图中MI值在各种设置下都接近下界，经验性地证明了基于JSD的估计是紧致的。$

与SOTA估计器的比较

在更复杂的连续高斯和非高斯分布（如cubic, asinh, uniform等）基准测试上，本文将新提出的下界估计器 $I_{CE}$ 与多种主流的MI变分下界估计器（如MINE, NWJ, InfoNCE等）进行了比较。

结果表明：

稳定性和低方差：本文的估计器 $I_{CE}$ 在所有测试场景中都表现出高度稳定和低方差的特性。相比之下，MINE和NWJ等传统VLB估计器在MI值较高或分布复杂时，估计值方差极大，甚至出现严重偏差。
可靠的下界：与会产生偏高估计的SMILE等方法不同，本文的估计器始终提供一个可靠的MI下界。如下图所示，在“阶梯式”MI变化场景中，本文的方法（橙色虚线）能稳定地追踪真实MI（黑色虚线）的下界，而其他方法则表现出较大的波动或偏差。

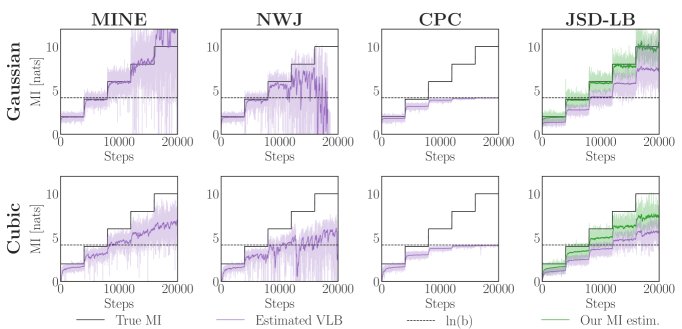
d=5，批次大小b=64的阶梯式MI估计比较。上排为高斯情况，下排为三次函数情况。

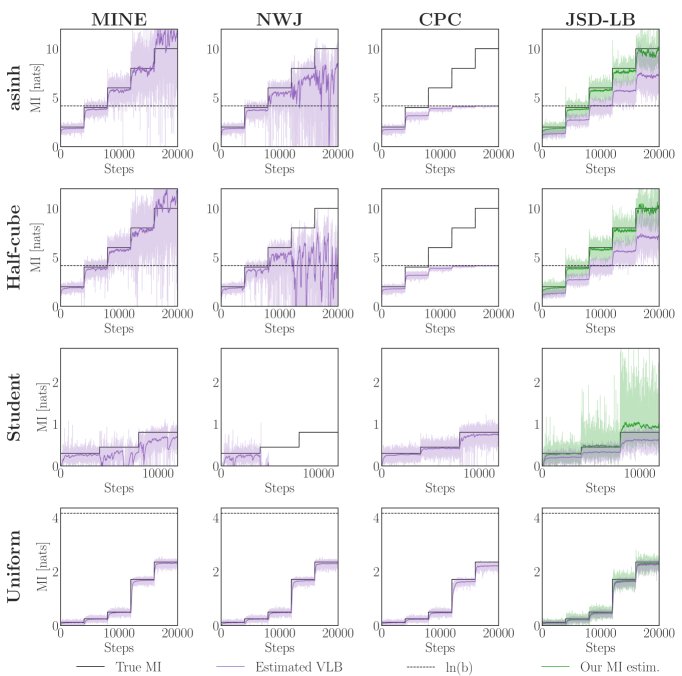
d=5，批次大小b=64的阶梯式MI估计比较，针对asinh、half-cube、学生t和均匀分布。

实际应用：信息瓶颈

实验还展示了将JSD目标应用于信息瓶颈（Information Bottleneck, IB）框架的实用价值。由于JSD目标的优化过程比其他MI下界更稳定，使用它作为IB的正则项可以在表示学习任务中取得更好的性能。

总结

总的来说，实验强有力地证明了本文提出的JSD-KLD下界是紧致的。基于此理论构建的MI估计器 $I_{CE}$ 不仅自身是一个稳定、低方差的可靠下界，也为那些在实践中行之有效的、基于JSD的判别式学习方法（如Deep InfoMax）提供了坚实的理论依据和更强的信心。