Cost-Aware Retrieval-Augmentation Reasoning Models with Adaptive Retrieval Depth
-
ArXiv URL: http://arxiv.org/abs/2510.15719v1
-
作者: Helia Hashemi; Victor Rühle; Saravan Rajmohan
-
发布机构: Microsoft
TL;DR
本文提出了一种成本感知的动态检索增强推理模型 Dynamic Search-R1,它通过强化学习动态调整检索文档的数量,在显著降低约16-20%延迟的同时,将精确匹配(Exact Match)准确率平均提升了约5%。
关键定义
- Dynamic Search-R1: 本文提出的核心模型,是 Search-R1 的扩展。它允许大语言模型(LLM)与搜索引擎进行更动态的交互,不仅能生成查询,还能通过生成一个特殊的\(<more info>\) Token来请求获取更多(更深层次)的检索结果,从而实现自适应的检索深度。
- Cost-Aware Advantage Function (成本感知的优势函数): 本文在强化学习(RL)框架中提出的核心创新。它修改了标准优势函数,引入一个成本惩罚项。这个函数不仅奖励正确的答案,还惩罚那些导致高计算成本(如过多的Tokens或高延迟)的生成序列。
- Memory-bound Cost (内存约束成本): 一种成本计算方式,直接将生成序列的总长度(包括模型生成的Tokens和检索返回的Tokens)作为成本。这种方式旨在最小化占用的GPU内存。
- Latency-bound Cost (延迟约束成本): 一种更精细的成本计算方式。它区分了模型“生成”一个Token和“编码”(处理)一个检索来的Token之间的延迟差异,并为它们分配不同的成本权重。实验表明,生成Token的延迟远高于编码Token,因此这种成本函数能更准确地反映模型的实际推理延迟。
相关工作
目前,结合了检索的增强生成(Retrieval-Augmented Generation, RAG)模型已成为提升大语言模型(LLM)准确性和事实性的标准技术。现有先进的检索增强推理模型,如 Search-R1,虽然能与搜索引擎交互,但其交互方式有限,即每次查询只能返回固定数量的文档。
这种固定数量的检索存在明显瓶颈:
- 信息不足: 对于复杂问题,少量文档可能无法提供足够信息,而模型无法主动请求更多。
- 效率低下与资源浪费: 对于简单问题,返回大量文档会造成不必要的计算开销和延迟,甚至可能因“中间丢失(loss-in-the-middle)”现象而降低性能。
本文旨在解决上述问题,通过让模型学习一种动态且具备成本意识的检索策略,使其能根据问题的需要自适应地决定检索文档的数量,从而在保证或提升效果的同时,显著提高模型的计算效率。
本文方法
本文在现有的检索增强推理模型 Search-R1 的基础上,提出了一个名为 Dynamic Search-R1 的新框架。其核心思想是赋予模型动态调整检索深度的能力,并通过一种成本感知的强化学习方法来训练模型,使其在效率和效果之间取得更好的平衡。
自适应检索深度
为了打破固定数量检索的限制,本文对模型的交互方式进行了扩展。除了生成常规的推理文本和 \(<search>\) 查询外,模型还可以生成一个特殊的 \(<more info>\) Token。这个Token允许模型请求获取当前查询结果中排名更靠后的 \(k\) 篇文档。
具体的交互流程如算法1所示,模型在一个推理循环中,可以根据中间的推理判断,决定是生成新的查询,还是在现有查询结果的基础上请求更多信息,或是给出最终答案。这种设计使得检索深度不再是固定的超参数,而是由模型根据具体问题动态决定的。
成本感知的优势函数
为了引导模型做出高效的决策,避免其无节制地请求更多信息,本文在强化学习的训练过程中引入了一个成本感知的优势函数(Cost-Aware Advantage Function)。
针对 GRPO 算法
对于组相对策略优化(Group Relative Policy Optimization, GRPO)算法,其优势函数被修改为:
\[A_{i}= \frac{r_{i}-\text{mean}(\{r_{1},r_{2},\cdots,r_{G}\})}{\text{std}(\{r_{1},r_{2},\cdots,r_{G}\})} -\alpha\left(\frac{c_{i}-\text{mean}(\{c_{1},c_{2},\cdots,c_{G}\})}{\text{std}(\{c_{1},c_{2},\cdots,c_{G}\})}\right)\]其中,$A_i$ 是第 $i$ 个模型输出的优势值,$r_i$ 是其奖励(如答案是否正确),$c_i$ 是其成本。$\alpha$ 是一个超参数,用于平衡奖励和成本的重要性。该公式的一个关键优点是相对归一化:它惩罚的是那些相对于同一问题的其他可能解法而言成本过高的输出,而不是绝对的高成本,从而能够适应不同难度的问题。
针对 PPO 算法
对于近端策略优化(Proximal Policy Optimization, PPO)算法,本文修改了Token级别的奖励函数。对于序列中的最后一个Token,其奖励被定义为:
\[r_{t} = \dots + \mathbf{1}\{t= \mid y \mid \}\cdot\max\{r\epsilon,r-\alpha c\}\]其中,$r$ 是最终答案的奖励(正确为1,错误为0),$c$ 是成本,$\alpha$ 是成本权重。这个设计确保了即使成本很高,正确的答案至少也能获得一个很小的正奖励 $\epsilon$(实验中设为0.2),从而稳定训练。
两种成本函数
本文探索了两种计算成本 $c$ 的方式:
- 内存约束成本 (Memory-bound Cost): 最简单的方式,成本 $c$ 等于总Token数 $ \mid y \mid $。它关注于最小化内存占用。
- 延迟约束成本 (Latency-bound Cost): 更精细的方式,公式为:$c_{i}=\sum_{t=1}^{ \mid y_{i} \mid }{I(y_{i,t})}\cdot c_{g}+\sum_{t=1}^{ \mid y_{i} \mid }{(1-I(y_{i,t}))}\cdot c_{e}$。这里,$c_g$ 是生成一个Token的平均延迟,而 $c_e$ 是处理(编码)一个输入Token的平均延迟。实验发现,生成Token的延迟比编码Token高出621%,因此该成本函数能更真实地反映模型的推理延迟。
实验结论
本文在7个不同的问答数据集上进行了实验,包括通用QA(如NQ、TriviaQA)和多跳QA(如HotpotQA、Musique)。
核心实验结果
实验结果表明,与基线模型 Search-R1 相比,本文提出的 Dynamic Search-R1 在效率和效果上均取得了显著提升。
下表展示了使用 GRPO 算法在三个数据集上的核心对比结果(EM:精确匹配率,Tokens:总Token数,Latency:延迟):
| 模型 | NQ (EM/Tokens/Latency) | PopQA (EM/Tokens/Latency) | Bamboodgle (EM/Tokens/Latency) |
|---|---|---|---|
| 基线模型 | |||
| Search-R1 | 0.480 / 1083 / 88.82 | 0.433 / 1273 / 96.29 | 0.196 / 1355 / 103.64 |
| 本文模型 | |||
| Dynamic Search-R1 (无成本惩罚) | 0.497 / 1387 / 102.98 | 0.469 / 1539 / 107.61 | 0.218 / 1592 / 115.36 |
| Dynamic Search-R1 - 内存约束 | 0.491 / 977 / 83.87 | 0.465 / 1064 / 91.10 | 0.215 / 1148 / 98.03 |
| Dynamic Search-R1 - 延迟约束 | 0.493 / 991 / 70.43 | 0.468 / 1095 / 82.86 | 0.212 / 1171 / 87.62 |
结果分析
- 动态检索的有效性: “无成本惩罚”的 Dynamic Search-R1 模型相比基线 Search-R1,在准确率(EM)上有所提升,但代价是消耗了更多的Tokens和更高的延迟。这证明了动态检索本身是有效的,但需要约束。
- 成本感知的优越性: 引入成本惩罚后,“内存约束”和“延迟约束”版本的模型在保持甚至超越基线准确率的同时,显著降低了Tokens消耗和延迟。
- 延迟约束成本更优: 对比两种成本函数,“延迟约束”版本在Tokens数量与“内存约束”版本相近的情况下,实现了更低的延迟。这验证了区分生成Token和编码Token成本的必要性和有效性。整体上,延迟约束模型在所有数据集上平均降低了16-20%的延迟,同时精确匹配率平均提升了约5%。
超参数影响
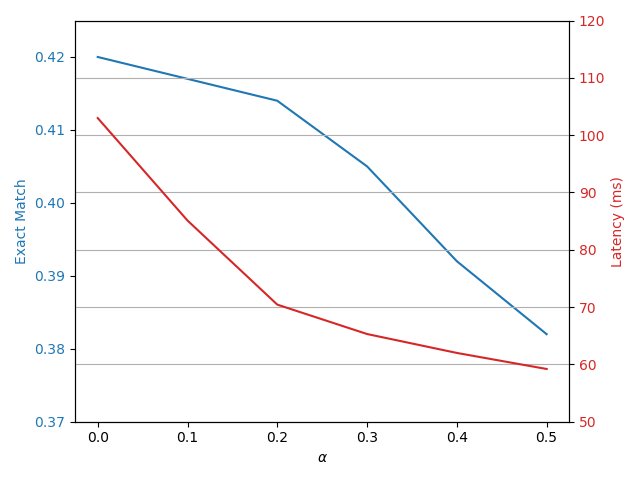
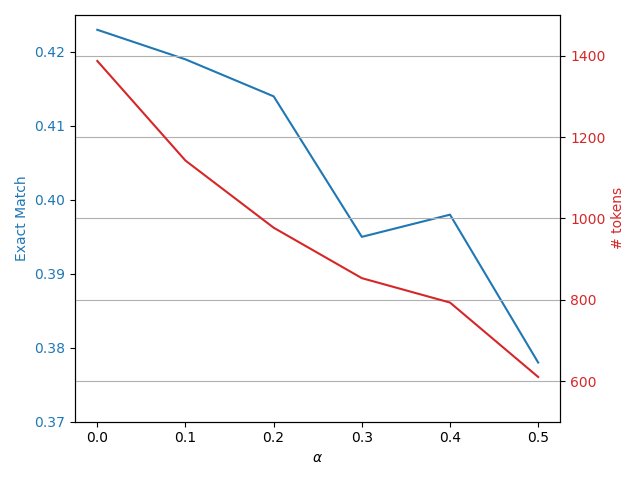
上图展示了成本权重 $\alpha$ 对模型性能的影响。随着 $\alpha$ 的增大,模型的延迟和Token消耗持续下降,而准确率(EM)则呈现先上升后下降的趋势。这表明存在一个最佳的 $\alpha$ 值,可以在显著提升效率的同时,最大化甚至超越原始模型的性能。
最终结论
本文提出的成本感知动态检索增强推理框架是成功的。通过赋予模型自适应调整检索深度的能力,并利用成本感知的强化学习进行优化,该方法在不牺牲甚至提升任务性能的前提下,显著提高了模型的推理效率(特别是延迟)。实验证明,更精细的“延迟约束”成本函数比简单的“内存约束”成本函数表现更佳。这些发现在不同大小的模型(3B和7B)和多个数据集中都得到了一致的验证。