Deep Self-Evolving Reasoning

• ArXiv URL: http://arxiv.org/abs/2510.17498v1

• 作者: Jiang Bian; Xumeng Wen; Zihan Liu; Yang Wang; Shun Zheng; Mao Yang

• 发布机构: Microsoft Research Asia; Peking University

---

TL;DR

本文提出了一种名为深度自进化推理（Deep Self-Evolving Reasoning, DSER）的概率框架，它将迭代推理建模为马尔可夫链，使即使是能力较弱的模型也能通过长时间的并行自进化过程，解决原本无法解决的复杂问题。

关键定义

• 深度自进化推理 (Deep Self-Evolving Reasoning, DSER)：一种概率性推理范式。它将模型的迭代推理（如验证-修正循环）视为一个在解空间中进行随机转换的马尔可夫链。其核心思想是，只要改进的概率（从错误解到正确解）略高于退化的概率（从正确解到错误解），通过足够多次的迭代，系统就能收敛到以正确解为主的稳定分布。通过并行运行多个长时程的自进化过程，可以放大这种微小的积极趋势，从而逐步逼近正确答案。

• 自进化随机过程 (Self-Evolving Stochastic Process)：本文用于描述迭代推理的核心数学模型。每个迭代步骤（即一次验证和修正）被看作是解状态的一次随机转换。该过程被具体化为一个马尔可夫链。

• 马尔可夫链公式化 (Markov Chain Formulation)：将解的状态简化为两个：正确（Correct, C）和不正确（Incorrect, I）。状态之间的转换由一个转移矩阵 \(P\) 定义，其中关键参数是改进概率 \(p_IC\)（从I到C）和退化概率 \(p_CI\)（从C到I）。该模型的核心在于，最终的稳定分布 \(π\) (即长期来看解为正确的概率) 只取决于这两个概率的比值，而非单步验证或修正的绝对准确率。

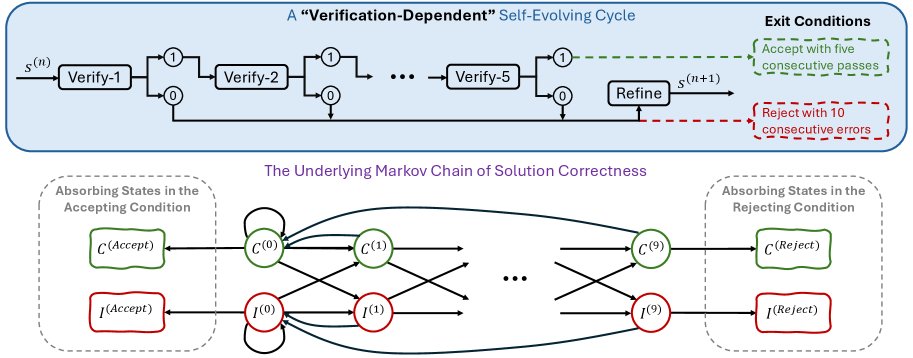
• 依赖验证的自进化 (Verification-Dependent Self-Evolving)：本文用来描述先前工作（如 Huang & Yang, 2025）所采用的框架。这类框架的迭代过程强依赖于模型自我验证的结果（通过或失败），并设置了硬性的终止条件（如连续失败10次则退出，连续通过5次则接受）。本文指出，这种机制对于能力较弱的模型在处理难题时，容易导致过早终止或接受错误答案，从而限制了其深度推理的潜力。

相关工作

当前，长思维链 (Chain-of-Thought, CoT) 推理已成为大语言模型（LLM）高级推理能力的基石。基于此，前沿的验证-修正 (verification–refinement) 框架已使顶尖的专有模型（如GPT-5，Gemini 2.5 Pro）能够解决奥林匹克竞赛级别的难题。

然而，这些框架的成功严重依赖于模型强大且可靠的自我验证和修正能力。对于目前可访问性更广的开源、中小型模型而言，这是一个巨大的瓶颈。在处理极难问题时，这些模型往往表现出自我验证能力弱、自我改进不稳定、指令遵循能力差等问题，导致它们在现有框架下容易意外终止或无法有效改进。

本文旨在解决的核心问题是：在模型自身的验证和修正能力较弱的情况下，如何能有效扩展其推理边界，使其能够解决原本超出其能力范围的复杂问题？

本文方法

本文提出的DSER方法将迭代式的验证与修正过程建模为一个自进化的随机过程，从而为能力有限的模型解决难题提供了理论上可行的路径。

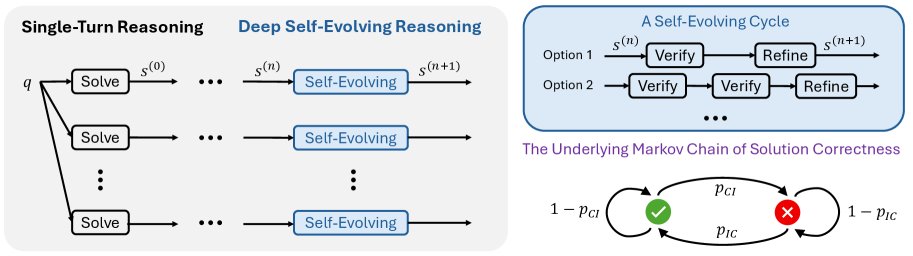
创新点：基于马尔可夫链的概率推理

与依赖单步验证结果的确定性框架不同，DSER的核心创新在于其概率性视角。

1. 过程建模：整个推理过程被视为一个马尔可夫链。解的状态空间被简化为两个：\(C\) (Correct) 和 \(I\) (Incorrect)。

   • 初始解 \(s^(0)\) 由模型直接生成：

     \[s^{(0)} = \mathcal{R}^{LLM}(q)\]

   • 在第 \(n\) 次迭代中，模型首先对当前解 \(s^(n)\) 进行自我验证，生成验证报告 \(v^(n)\)：

     \[v^{(n)} = \mathcal{R}^{LLM}([q; s^{(n)}; p_v])\]

   • 然后，基于验证报告，模型进行修正，生成新解 \(s^(n+1)\)：

     \[s^{(n+1)} = \mathcal{R}^{LLM}([q; s^{(n)}; p_v; v^{(n)}; p_r])\]

   这个 \(s^(n) -> s^(n+1)\) 的转换构成马尔可夫链的一个步骤。

2. 收敛性分析：该过程的动态由一个2x2的转移概率矩阵 \(P\) 控制：

   \[P = \begin{pmatrix} P(C \mid C) & P(I \mid C) \\ P(C \mid I) & P(I \mid I) \end{pmatrix} = \begin{pmatrix} 1-p_{CI} & p_{CI} \\ p_{IC} & 1-p_{IC} \end{pmatrix}\]

   其中，\(p_IC\) 是从错误解改进为正确解的概率，\(p_CI\) 是从正确解退化为错误解的概率。

   只要马尔可夫链是遍历的（即 \(p_IC > 0\) 且 \(p_CI > 0\)），它将收敛到一个唯一的稳定分布 \(π = [π_C, π_I]\)，其中解为正确的长期概率为：

   \[\pi_C = \frac{p_{IC}}{p_{IC} + p_{CI}}\]

优点

• 对不完美验证的鲁棒性：DSER的成功不依赖于单次验证或修正的成功。理论上，只要改进的倾向性 (\(p_IC\)) 略微大于退化的倾向性 (\(p_CI\))，经过足够长的迭代，正确的解就会在分布中占据主导地位。这为通过多数投票获得正确答案提供了理论保障。
• 发掘“群体智慧”：实践中发现，即使 \(p_IC < p_CI\)，只要 \(p_IC\) 不为零，通过并行运行多个DSER过程并进行多数投票，仍可能得到正确答案。因为正确的解会收敛到唯一的基准真相，而错误的解则会发散到各种不同的结果中。
• 避免过早终止：与“依赖验证的自进化”方法相比，DSER避免了因验证不准而导致的过早退出（拒绝）或过早收敛于错误答案（接受）。它允许模型在“困惑”时进行更深度的探索，从而有机会找到正确路径。

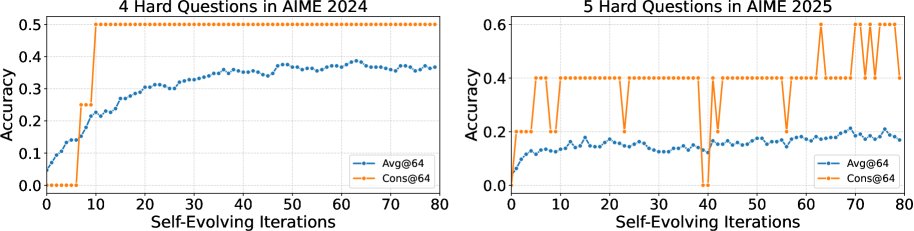
实验结论

本文使用一个8B参数的强大开源模型在AIME 2024和2025数学竞赛基准上进行了实验。该模型在基线上无法解决其中的9个难题。

• 突破推理极限：DSER成功解决了这9个“无法解决”问题中的5个。其中一个问题在初始测试中Pass@1的成功率为0。这证明DSER有效扩展了模型单次推理的能力边界。

• 提升整体性能：将DSER应用于整个AIME基准测试时，模型的整体性能得到显著提升。在AIME 2024上，Pass@1准确率提升了6.5%（从82.8%到89.3%）；在AIME 2025上，提升了9.0%（从74.4%到83.4%）。值得注意的是，通过DSER和多数投票，这个8B模型的最终准确率甚至超过了其600B参数的教师模型的单次推理准确率。

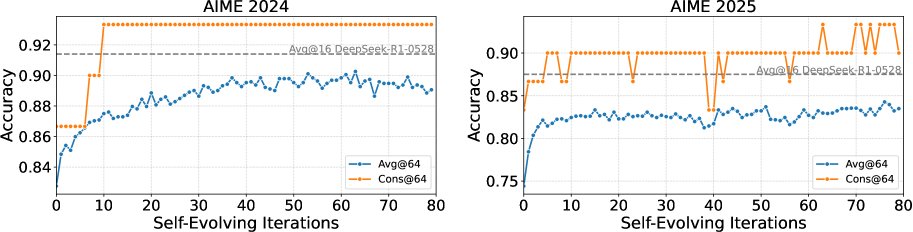
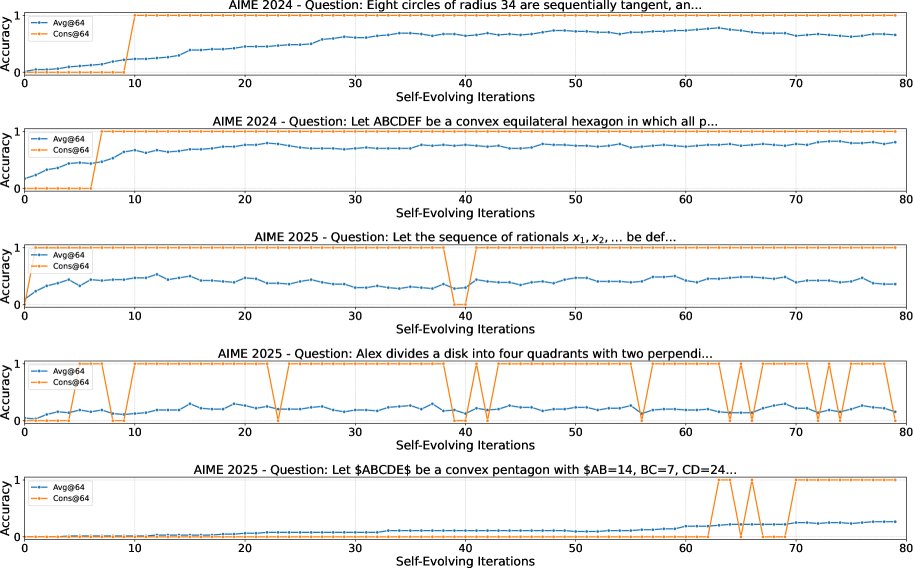
• 收敛行为多样性：对具体问题的分析表明，不同问题的收敛速度和稳定分布各不相同。有些问题能快速收敛到高正确率，而另一些问题收敛缓慢，或稳定在正确与错误解混合的状态。即便如此，多数投票机制依然有效。

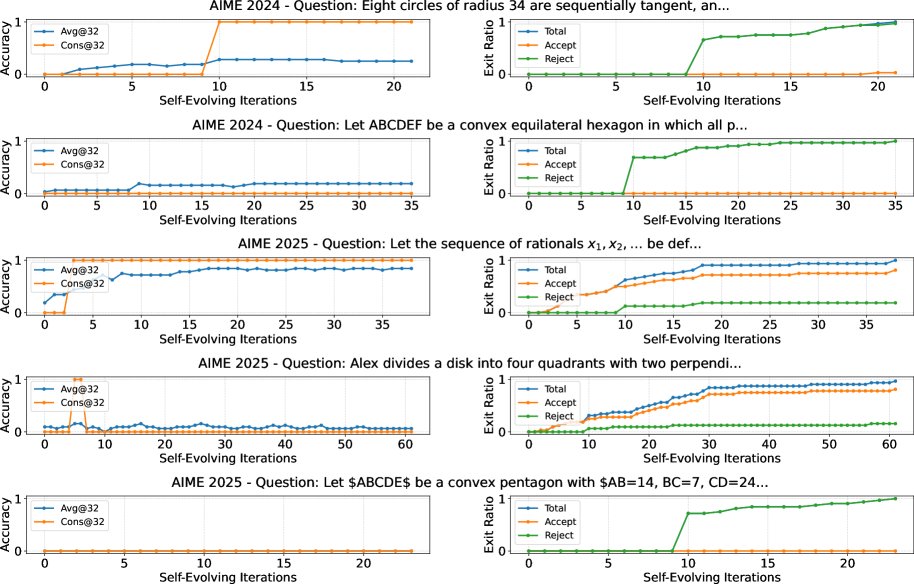
• 优于依赖验证的方法：在相同的9个难题上，“依赖验证的自进化”方法仅解决了2个。实验表明，该方法在处理超出模型能力的问题时，由于验证不可靠，会频繁出现过早退出或接受错误答案的情况，验证了DSER框架的优越性。

• 最终结论：DSER是一个有效的框架，它通过增加测试时计算量，显著扩展了中小型开源模型的推理能力，使其能够解决原本无法企及的难题。该工作不仅提供了一种实用的性能提升方法，也揭示了当前开源模型在自我验证和修正能力上的根本局限，为未来模型训练指明了方向——开发具备更强内在自进化能力的模型。