DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

• ArXiv URL: http://arxiv.org/abs/2402.03300v3

• 作者: Mingchuan Zhang; R. Xu; Zhihong Shao; Jun-Mei Song; Qihao Zhu; Y. K. Li; Peiyi Wang; Yu Wu; Daya Guo

• 发布机构: DeepSeek-AI; Peking University; Tsinghua University

---

TL;DR

本文介绍了DeepSeekMath，一个通过在精心构建的120B数学语料上进行持续预训练，并采用一种名为GRPO的新型高效强化学习算法，从而将开源模型的数学推理能力推向接近GPT-4水平的7B语言模型。

关键定义

• DeepSeekMath Corpus: 一个大规模、高质量的数学预训练语料库，包含120B token。它通过一个精心设计的迭代式数据筛选流程，从公开的Common Crawl网络数据中提取而来。该语料库是多语言的，且经过严格的去污染处理，是本文模型取得优异数学能力的基础。
• 组相对策略优化 (Group Relative Policy Optimization, GRPO): 本文提出的一种强化学习算法，是近端策略优化（PPO）的一个变体。其核心创新在于移除了PPO中的评论家模型（critic model），转而通过对同一问题生成的多个（一组）答案的得分进行评估，使用这组分数的平均值作为基线（baseline）来估计优势函数。这种设计显著降低了训练过程中的内存消耗和计算负担，实现了更高效的强化学习。

相关工作

当前，顶尖的语言模型如GPT-4和Gemini-Ultra在数学推理方面表现出色，但它们是闭源的，其技术细节和模型权重均未公开。与此同时，现有的开源模型在数学能力上与这些顶尖模型存在显著的性能差距，这构成了该领域的一个关键瓶颈。

本文旨在解决这一具体问题：缩小开源社区与最先进闭源模型在数学推理能力上的差距。通过构建一个更强大、公开可用的数学专用基础模型，推动相关领域的研究和应用。

本文方法

本文通过一个三阶段流程来构建和优化DeepSeekMath模型：大规模数学预训练、监督微调（SFT）和基于GRPO的强化学习（RL）。

阶段一：大规模数学预训练

DeepSeekMath语料库构建

为了获得高质量的数学预训练数据，本文设计了一个从Common Crawl (CC) 中挖掘数学网页的迭代式流程。

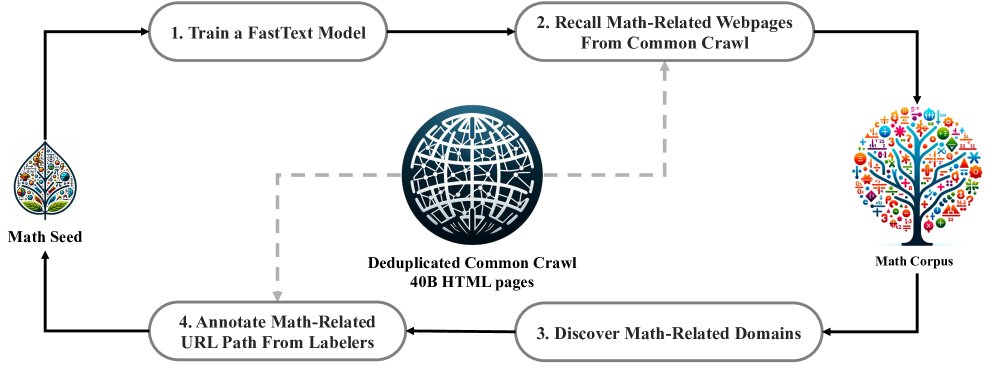
1. 初始阶段：使用一个高质量的数学文本集合OpenWebMath作为种子语料，训练一个fastText分类器，用于从海量CC数据中初步召回与数学相关的网页。
2. 迭代优化：为了提升分类器的多样性和准确性，本文分析了初次召回的网页所属的域名，将数学内容占比较高的域名（如 \(mathoverflow.net\)）识别出来。然后，通过人工标注这些域名下的特定URL模式，将更多未被召回的数学网页补充到种子语料中。
3. 循环与终止：用扩充后的种子语料重新训练分类器，并进行下一轮数据挖掘。此过程重复四次，直到新召回的数据量趋于饱和（第四轮约98%的数据已在第三轮被收集）。最终构建了包含120B token的DeepSeekMath语料库。
4. 数据去污染：为保证评估的公正性，严格过滤了语料库中与已知数学基准测试（如GSM8K, MATH）问题或答案匹配的n-gram片段。

DeepSeekMath-Base模型训练

训练的起点并非通用语言模型，而是代码预训练模型 \(DeepSeek-Coder-Base-v1.5 7B\)。本文发现，从代码模型开始训练，比从通用模型开始能获得更好的数学能力。

基础模型 \(DeepSeekMath-Base 7B\) 在一个混合数据集上持续训练了500B token，数据构成如下：

• 56% 来自DeepSeekMath语料库
• 20% 来自Github代码
• 10% 来自arXiv论文
• 10% 来自通用的中英文自然语言数据
• 4% 来自AlgebraicStack（数学代码）

这种混合训练不仅提升了数学能力，还保持了强大的代码能力，并增强了模型的通用推理能力。

阶段二：监督微调 (SFT)

在预训练获得强大的 \(DeepSeekMath-Base\) 模型后，本文构建了一个包含776K样本的数学指令微调数据集对其进行SFT，产出 \(DeepSeekMath-Instruct 7B\) 模型。

该数据集覆盖了英汉双语的K-12数学问题，其特点是解题步骤格式多样，包括：

• 思维链 (Chain-of-Thought, CoT): 详细的文本推理步骤。
• 程序思维 (Program-of-Thought, PoT): 通过编写代码来解决问题。
• 工具集成推理 (Tool-integrated reasoning): 结合自然语言和代码工具进行求解。

阶段三：强化学习 (RL)

为了进一步激发模型的潜力，本文提出了创新的GRPO算法，并用其训练得到最终的 \(DeepSeekMath-RL 7B\) 模型。

组相对策略优化 (GRPO)

PPO算法需要一个与策略模型大小相当的评论家模型来估计值函数，这带来了巨大的资源开销。GRPO通过以下方式解决了这个问题：

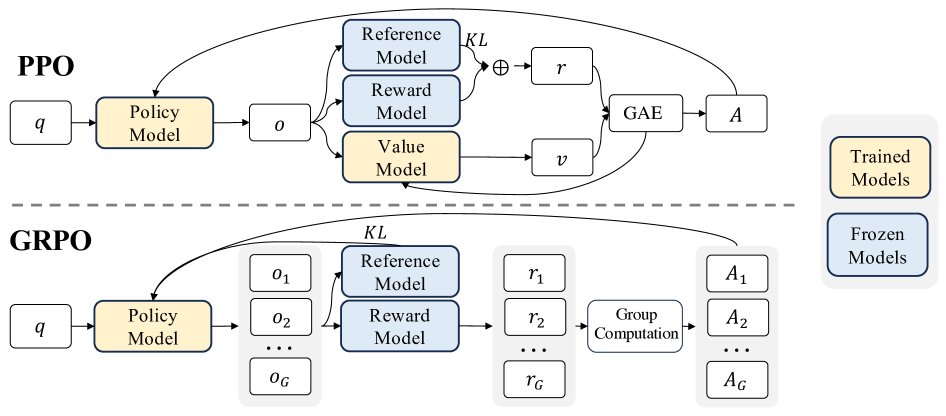
• 核心机制：对于每个问题，GRPO不再依赖评论家模型，而是让当前策略模型生成一组（例如64个）不同的答案。然后，一个奖励模型（reward model）为这些答案打分。
• 优势估计：GRPO使用这组答案的平均奖励作为基线（baseline）。每个答案的优势（advantage）就是其自身奖励与该组平均奖励的差值。这个相对优势 \($\hat{A}\_{i,t}\)$ 被用来指导策略模型的优化。
• 目标函数：GRPO的优化目标是最大化以下函数，其中包含了PPO的裁剪（clip）机制以稳定训练，并直接加入了与参考模型的KL散度作为正则项。

\[\mathcal{J}_{GRPO}(\theta)=\mathbb{E}_{[q \sim P(Q),\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(O \mid q)]} \frac{1}{G}\sum_{i=1}^{G}\frac{1}{ \mid o_{i} \mid }\sum_{t=1}^{ \mid o_{i} \mid }\left\{\min\left[\frac{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} \mid q,o_{i,<t})}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} \mid q,o_{i,<t})},1-\varepsilon,1+\varepsilon\right)\hat{A}_{i,t}\right]-\beta\mathbb{D}_{KL}\left[\pi_{\theta} \mid \mid \pi_{ref}\right]\right\}\]

这种方法将优势函数的计算与比较数据的内在结构对齐，且因无需训练评论家模型而变得极为高效。

DeepSeekMath-RL模型训练

\(DeepSeekMath-RL\) 模型是在 \(DeepSeekMath-Instruct 7B\) 的基础上，仅使用SFT数据中与GSM8K和MATH相关的CoT格式问题进行GRPO训练得到的。这一受限的训练数据设置有助于检验RL阶段的泛化能力。

实验结论

本文通过在多个标准数学基准上的全面评估，验证了其方法在各个阶段的有效性。

预训练阶段的有效性

• 语料库质量：\(DeepSeekMath-Base 7B\) 在仅经过预训练后，其性能在多个数学基准上全面超越了所有开源基础模型，包括参数量更大的 \(Llemma 34B\)。
• 超越大型闭源模型：值得注意的是，7B的 \(DeepSeekMath-Base\) 在竞赛级MATH基准测试上取得了36.2%的准确率，甚至超过了规模大77倍的闭源模型 \(Minerva 540B\)（33.6%），这充分证明了DeepSeekMath语料库的高质量和预训练策略的成功。

模型	大小	GSM8K	MATH	MMLU STEM	CMATH
闭源基础模型
Minerva	540B	58.8%	33.6%	63.9%	-
开源基础模型
Mistral	7B	40.3%	14.3%	51.1%	44.9%
Llemma	34B	54.0%	25.3%	52.9%	56.1%
DeepSeekMath-Base	7B	64.2%	36.2%	56.5%	71.7%

表1: DeepSeekMath-Base 7B与强力基础模型的性能对比

• 代码训练的增益：实验表明，在进行数学训练之前先进行代码训练，能够显著提升模型在有工具和无工具环境下的数学推理能力。
• 工具使用和形式数学能力：\(DeepSeekMath-Base 7B\) 在利用Python解决数学问题（GSM8K+Python 66.9%, MATH+Python 31.4%）和形式化证明（miniF2F-test 24.6%）方面也表现出领先性能。

模型	大小	GSM8K+Python	MATH+Python	miniF2F-test
CodeLlama	34B	52.7%	23.5%	18.0%
Llemma	34B	64.6%	26.3%	21.3%
DeepSeekMath-Base	7B	66.9%	31.4%	24.6%

表2: 工具使用和形式化证明能力对比

SFT和RL阶段的有效性

\(DeepSeekMath-RL 7B\) (最终模型) 在所有开源模型中取得了最佳性能，并接近甚至超过了一些强大的闭源模型。

• 无工具推理：在不允许使用外部工具的思维链推理中，\(DeepSeekMath-RL 7B\) 在MATH上取得了51.7%的准确率，这是开源模型首次在该高难度基准上突破50%大关。此成绩超越了所有7B到70B的开源模型，以及Gemini Pro、GPT-3.5等闭源模型。
• 工具集成推理：在使用工具时，\(DeepSeekMath-RL 7B\) 在MATH上的准确率达到58.8%，同样领先于所有现有开源模型。
• GRPO的泛化能力：尽管RL训练数据仅限于GSM8K和MATH的CoT格式，但最终模型在所有测试基准上（包括未见过的中文数学题CMATH和工具使用场景）都比SFT模型有显著提升。这证明了GRPO算法带来的能力提升具有很强的泛化性。

模型	大小	GSM8K (CoT)	MATH (CoT)	MGSM-zh (CoT)	CMATH (CoT)
闭源模型
Gemini Ultra	-	94.4%	53.2%	-	-
GPT-4	-	92.0%	52.9%	-	86.0%
GLM-4	-	87.6%	47.9%	-	-
开源模型
InternLM2-Math	20B	82.6%	37.7%	-	-
Qwen	72B	78.9%	35.2%	-	-
MetaMath	70B	82.3%	26.6%	66.4%	70.9%
本文模型
DeepSeekMath-Instruct (SFT)	7B	82.9%	46.8%	73.2%	84.6%
DeepSeekMath-RL (RL)	7B	88.2%	51.7%	79.6%	88.8%

表3: 最终模型与顶尖模型的思维链推理性能对比

最终结论：本文通过高质量的数据工程、巧妙的预训练策略以及高效的强化学习算法GRPO，成功地将一个7B参数量的开源模型在数学推理能力上提升到了业界顶尖水平，为开源社区提供了强大且可复现的数学基础模型。