DELTA: Decoupling Long-Tailed Online Continual Learning

• ArXiv URL: http://arxiv.org/abs/2404.04476v1

• 作者: Percy Liang; Yann Dubois; Bal’azs Galambosi; Tatsunori Hashimoto

• 发布机构: Purdue University

---

TL;DR

本文提出了一种名为 DELTA 的解耦学习框架，通过两阶段训练策略（监督对比学习 + 均衡损失）有效解决了长尾在线持续学习（Long-Tailed Online Continual Learning, LTOCL）中的灾难性遗忘和类别不平衡问题。

关键定义

• 长尾在线持续学习 (Long-Tailed Online Continual Learning, LTOCL)：一个具有挑战性的学习场景，模型需要从一个类别极度不平衡（长尾分布）且顺序到来的数据流中持续学习新知识。在此设定下，每个数据样本仅被用于训练一次，且模型无法预知任务的整体数据分布。
• DELTA：本文提出的方法名称，是一种解耦长尾在线持续学习的框架。它采用两阶段训练策略：第一阶段通过对比学习来学习高质量的特征表示，第二阶段则专注于训练一个均衡的分类器。
• 均衡损失 (Equalization Loss, $L_{EQ}$)：本文提出的一种新颖损失函数，用于解决 LTOCL 中的偏置学习问题。它受均衡 Softmax 损失的启发，但专为在线场景设计。通过在计算损失前，利用当前批次的类别分布动态调整 logits，该损失能够为少数类样本分配更大的梯度，从而缓解模型对多数类的偏好。
• 多样本配对学习 (Multi-Exemplar Learning)：本文提出的一种样本选择策略。在训练时，将每个当前任务的样本与存储器中不止一个（而是多个）的旧样本（exemplar）进行配对。该策略旨在通过增加批次大小和多样性来平衡批次内的数据分布，稳定梯度估计，并提升模型的泛化能力。

相关工作

目前，在线持续学习 (Online Continual Learning, OCL) 的研究主要分为基于正则化的方法和基于记忆（回放）的方法。这些方法通常假设数据类别是均衡分布的，这限制了它们在真实世界长尾数据场景中的应用。

另一方面，长尾分类研究提出了多种解决类别不平衡的策略，如重采样、重加权和两阶段学习。然而，这些方法大多需要预先知道整个数据集的全局分布信息，这在数据以流式、单次处理方式出现的 OCL 场景中是不可行的。

因此，现有研究在处理兼具在线（单次过数据）、持续（任务序列）和长尾（类别严重不平衡）这三个特性的 LTOCL 问题上存在明显空白。本文旨在填补这一空白，解决模型在长尾数据流中学习时，既要避免灾难性遗忘又要克服对头（head）部类别过拟合的难题。

本文方法

为了应对 LTOCL 的挑战，本文提出了 DELTA 框架，其核心思想是将表示学习与分类器学习解耦，分为两个阶段进行训练。

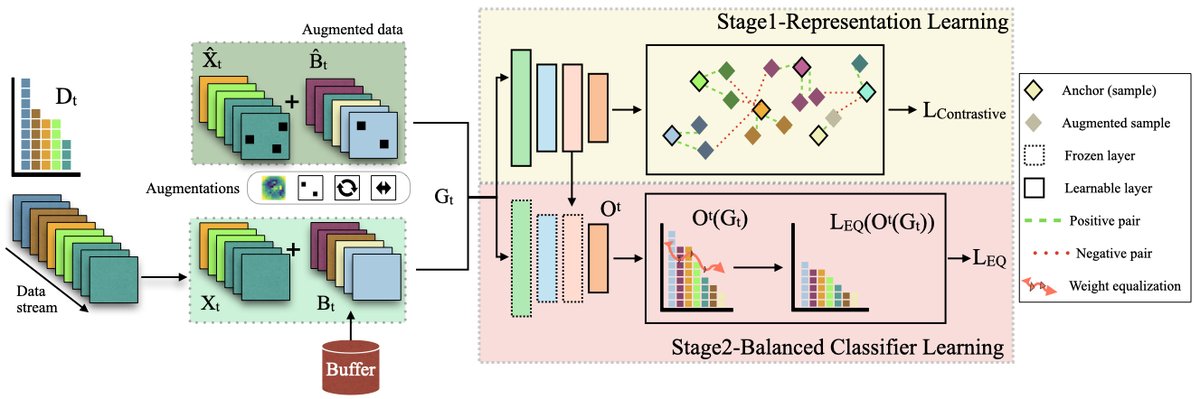
上图展示了 DELTA 框架的概览。在处理任务 $t$ 时，当前批次的样本 $X_t$ 与从记忆存储器 $B_t$ 中检索的样本及其增强版本混合，形成组合数据 $G_t$。该数据流经两阶段训练流程。

第一阶段：表示学习

此阶段的目标是在长尾和单次过数据的条件下学习到有效的特征表示。

• 方法：采用监督对比学习 (Supervised Contrastive Learning)，其灵感来源于 SimCLR。通过将同类样本（正样本）在表示空间中拉近，将不同类样本（负样本）推远，模型能够学习到更具判别力的特征。这对于样本稀少的尾（tail）部类别尤其有益。
• 损失函数：此阶段使用对比损失 $L_{contrastive}$ 进行优化。

\[L_{contrastive}(Z_{T})=\sum_{j\in T}\frac{-1}{ \mid P(j) \mid }\sum_{p\in P(j)}\frac{exp(v_{j}\cdot v_{p}/\tau)}{\sum_{k\in A(j)}exp(v_{j}\cdot v_{k}/\tau)}\]

其中 $v$ 是样本经过编码器和投影网络后的表示向量，$\tau$ 是温度超参数。

第二阶段：均衡分类器学习

在第一阶段学习到高质量的特征表示后，此阶段的目标是训练一个在类别间表现均衡的分类器。

• 方法：采用解耦策略，冻结编码器层的所有参数，仅对分类器层进行训练。
• 创新点：均衡损失 ($L_{EQ}$)：为解决传统交叉熵损失在不平衡数据上偏向多数类的问题，本文设计了均衡损失。它无需全局数据分布，而是根据当前训练批次（包含新数据和回放样本）的类别动态调整。

  1. 首先，计算当前批次数据 $D_t$ 的临时类别分布向量 $P(k^t)$：

     \[D_{t} = [n_{1}, n_{2}, ..., n_{h}]\] \[P(k^{t}) = [\frac{n_{1}}{\sum_{i=1}^{h}n_{i}},\frac{n_{2}}{\sum_{i=1}^{h}n_{i}},...,\frac{n_{h}}{\sum_{i=1}^{h}n_{i}}]\]

     其中 $n_h$ 是类别 $h$ 在当前批次中的样本数。

  2. 然后，在计算 Softmax 之前，将该分布向量作为先验添加到分类器的输出 logits $O^t(I_x)$ 上：

     \[L_{EQ} = -\sum_{i=1}^{N}\log\frac{e^{O^{t}(I_{x_{i}})[I_{y_{i}}] + \log(P(k^{t})[I_{y_{i}}])}}{\sum_{j=1}^{C}e^{O^{t}(I_{x_{i}})[j] + \log(P(k^{t})[j])}}\]

  通过这种方式，批次中样本数量较多的类别会获得较小的梯度，而样本数量较少的类别会获得较大的梯度，从而有效纠正了学习过程中的偏差。

多样本配对学习

为了进一步缓解训练数据（长尾）与测试数据（均衡）之间的分布差异，本文探索了多样本配对策略。

• 方法：对于每一个新任务的输入样本，从记忆存储器中检索并配对多个（而不是传统的一个）旧样本共同组成一个训练批次。
• 优点：
  1. 增大了有效的批次大小，有助于稳定梯度估计。
  2. 更好地平衡了每个批次内的类别构成，减少了模型对训练数据长尾特性的过拟合。
  3. 通过对回放样本的多次暴露和数据增强，有助于对抗灾难性遗忘。

实验结论

本文在 Split CIFAR-100-LT 和 VFN-LT 这两个长尾数据集上进行了广泛实验，验证了 DELTA 方法的有效性。

• 主要性能：如下表所示，在各种设置下，DELTA 的平均准确率显著优于现有的 OCL 方法（如 OnPRO, SCR, ASER 等）。现有方法在长尾场景下性能下降严重，而 DELTA 表现出强大的鲁棒性，性能增益明显。

方法	CIFAR100-LT						VFN-LT
	20 任务	20 任务	20 任务	10 任务	10 任务	10 任务	15 任务	15 任务	15 任务	7 任务	7 任务	7 任务
	M=0.5K	M=1K	M=2K	M=0.5K	M=1K	M=2K	M=0.5K	M=1K	M=2K	M=0.5K	M=1K	M=2K
OnPRO[ICCV ’23]	14.02 $0.44$	16.28 $\pm$ 0.81	18.01 $\pm$ 0.22	16.53 $\pm$ 0.55	16.92 $\pm$ 0.08	18.85 $\pm$ 0.32	11.93 $\pm$ 0.04	12.77 $\pm$ 0.07	13.50 $\pm$ 0.05	8.02 $\pm$ 0.60	9.38 $\pm$ 0.21	11.84 $\pm$ 0.49
SCR[CVPRW ’21]	12.22 $\pm$ 0.72	13.48 $\pm$ 0.90	15.88 $\pm$ 0.79	16.65 $\pm$ 0.90	17.02 $\pm$ 0.77	17.58 $\pm$ 0.66	11.55 $\pm$ 0.17	11.82 $\pm$ 0.10	12.39 $\pm$ 0.73	7.71 $\pm$ 0.49	9.19 $\pm$ 0.46	9.48 $\pm$ 0.47
ASER[AAAI ’21]	8.86 $\pm$ 0.30	7.86 $\pm$ 0.61	8.18 $\pm$ 0.31	12.68 $\pm$ 0.70	13.76 $\pm$ 0.01	15.90 $\pm$ 0.91	6.85 $\pm$ 0.34	7.61 $\pm$ 0.38	7.22 $\pm$ 0.36	7.46 $\pm$ 1.18	7.52 $\pm$ 1.09	6.35 $\pm$ 0.19
PRS[ECCV ’20]	7.61 $\pm$ 0.09	7.54 $\pm$ 0.21	7.03 $\pm$ 0.13	7.34 $\pm$ 0.92	8.95 $\pm$ 0.33	9.01 $\pm$ 0.39	7.17 $\pm$ 0.83	8.72 $\pm$ 0.15	8.39 $\pm$ 0.19	7.85 $\pm$ 0.50	8.66 $\pm$ 0.22	9.21 $\pm$ 0.30
CBRS[ICML ’20]	8.51 $\pm$ 0.19	8.66 $\pm$ 0.61	8.91 $\pm$ 0.33	9.50 $\pm$ 0.48	7.22 $\pm$ 0.43	7.31 $\pm$ 0.08	8.12 $\pm$ 0.94	8.35 $\pm$ 0.33	8.18 $\pm$ 0.44	7.52 $\pm$ 0.11	7.64 $\pm$ 0.08	7.92 $\pm$ 0.34
GSS[NeurIPS ’19]	5.16 $\pm$ 0.10	5.22 $\pm$ 0.22	5.09 $\pm$ 0.21	8.97 $\pm$ 0.65	10.12 $\pm$ 0.02	9.96 $\pm$ 0.47	5.86 $\pm$ 0.30	6.01 $\pm$ 0.91	5.86 $\pm$ 0.06	5.92 $\pm$ 0.54	4.30 $\pm$ 0.22	4.66 $\pm$ 0.60
LT-CIL(offline)	3.01 $\pm$ 0.77	2.67 $\pm$ 0.04	2.43 $\pm$ 0.02	1.76 $\pm$ 0.11	2.36 $\pm$ 0.25	3.76 $\pm$ 0.22	1.82 $\pm$ 0.45	2.02 $\pm$ 0.44	2.38 $\pm$ 0.08	3.08 $\pm$ 0.71	2.92 $\pm$ 0.04	1.99 $\pm$ 0.31
DELTA (本文方法)	16.53 $\pm$ 0.01	17.71 $\pm$ 0.11	19.93 $\pm$ 0.07	20.25 $\pm$ 0.71	21.06 $\pm$ 0.23	22.47 $\pm$ 0.51	12.5 $\pm$ 0.01	13.45 $\pm$ 0.02	13.84 $\pm$ 0.01	8.00 $\pm$ 0.39	10.41 $\pm$ 0.52	12.84 $\pm$ 0.54

• 偏差分析：混淆矩阵（下图）显示，相比于 OnPro 和 CBRS 等单阶段方法，DELTA 对新任务的偏置明显更小。其他方法倾向于将大量样本错误地分类到最新学习的类别中，而 DELTA 的解耦学习架构有效缓解了这一问题。

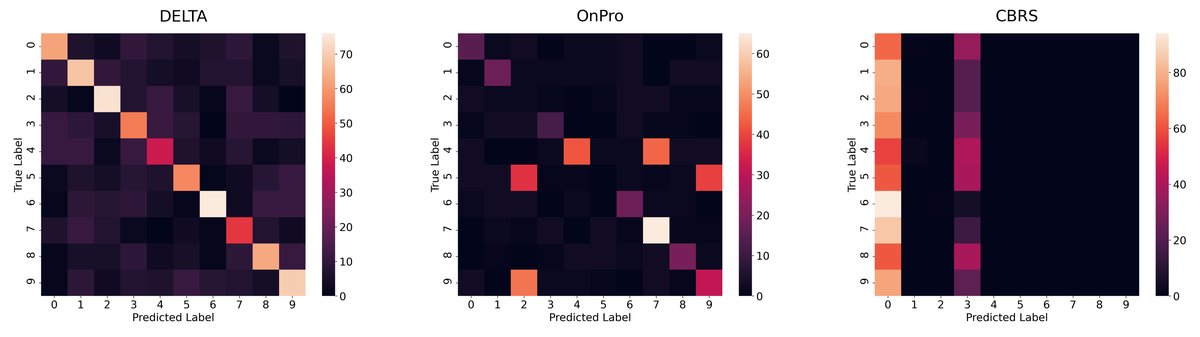
• 消融实验：
  • 均衡损失的有效性：用标准交叉熵损失替换均衡损失后，模型性能显著下降（CIFAR100-LT上准确率从19.93%降至16.62%），证明了 $L_{EQ}$ 的关键作用。
  • 对不同不平衡度的鲁棒性：在不同不平衡比 $\rho$ 下，DELTA 均表现出色。随着不平衡加剧（$\rho$ 变小），DELTA 相较于其他方法的优势愈发明显。
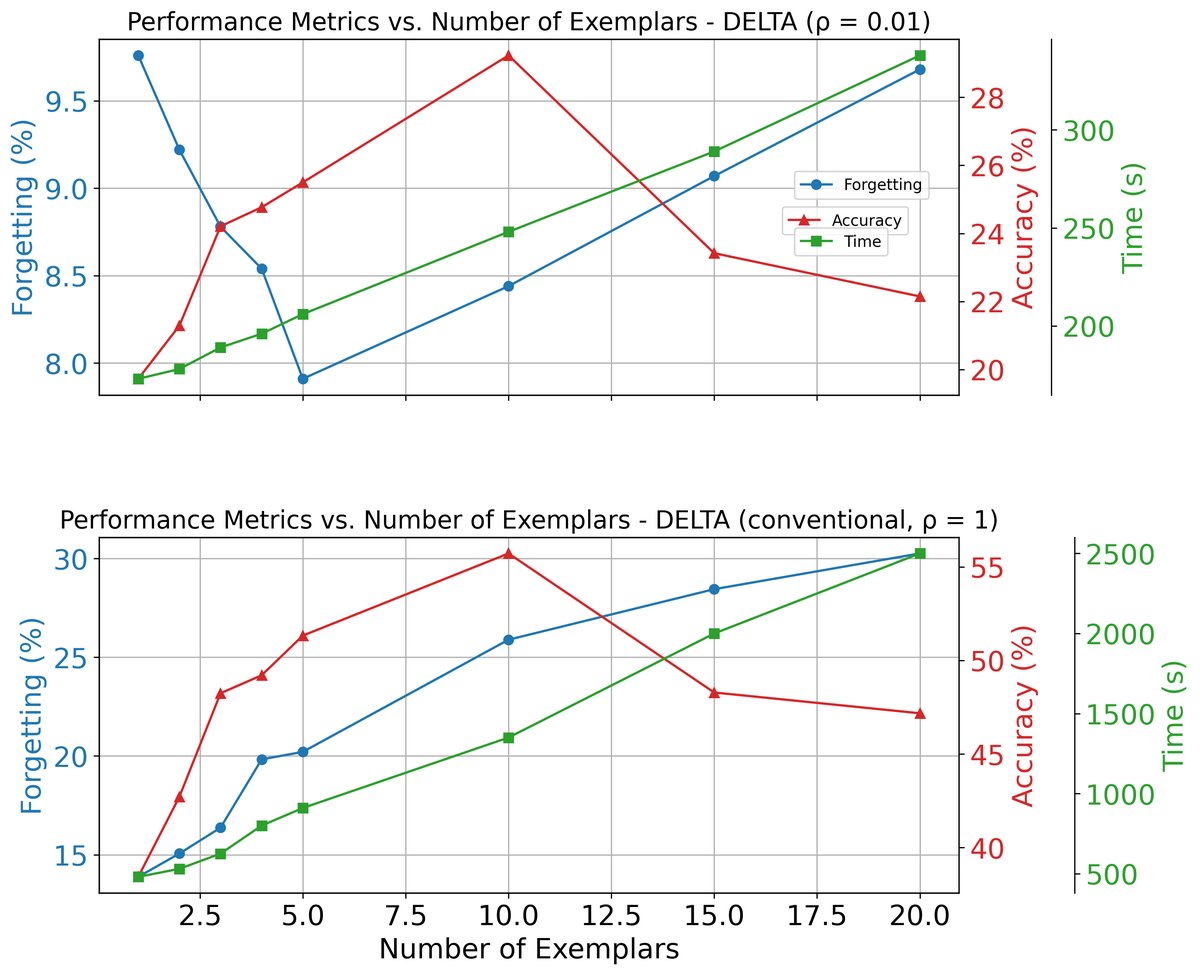
  • 多样本配对分析：在长尾场景下，增加每个输入样本配对的旧样本数量（在10个以内），可以持续提升模型准确率，但会增加训练时间。这证明了该策略在平衡批量数据分布和提升性能方面的潜力。

• 最终结论：本文提出的 DELTA 框架通过其创新的两阶段解耦学习和均衡损失函数，成功应对了长尾在线持续学习的挑战，在多个基准上取得了 SOTA 性能。实验证明，该方法能有效学习高质量表示，并训练出偏差更小的分类器，为 OCL 在现实世界中的应用展示了巨大潜力。