Direct Preference Optimization: Your Language Model is Secretly a Reward Model

• ArXiv URL: http://arxiv.org/abs/2305.18290v3

• 作者: Archit Sharma; E. Mitchell; Rafael Rafailov; Chelsea Finn; Christopher D. Manning; Stefano Ermon

• 发布机构: CZ Biohub; Stanford University

---

TL;DR

本文提出了一种名为直接偏好优化（DPO）的新算法，它通过一个解析性的映射关系，将传统强化学习中带约束的奖励最大化问题，巧妙地转化为一个简单的分类损失函数，从而无需显式训练奖励模型或进行复杂的强化学习，就能高效地使语言模型与人类偏好对齐。

关键定义

本文的核心在于对现有强化学习对齐框架的重新表述，其中关键定义如下：

• KL约束下的奖励最大化 (KL-constrained reward maximization)：这是强化学习从人类反馈（RLHF）中的标准优化目标。其目标是训练一个策略 $\pi$ 来最大化奖励函数 $r(x,y)$ 的期望值，同时通过一个KL散度惩罚项，限制策略 $\pi$ 与初始的参考策略 $\pi_{\text{ref}}$ 不会偏离太远。该目标可以表示为：

  \[\max_{\pi_{\theta}}\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta}(y\mid x)} \bigl{[}r_{\phi}(x,y)\bigr{]}-\beta\mathbb{D}_{\textrm{KL}}\bigl{[}\pi_{\theta }(y\mid x)\mid\mid\pi_{\text{ref}}(y\mid x)\bigr{]}\]

  其中 $\beta$ 是控制KL惩罚强度的系数。

• 布拉德利-特里模型 (Bradley-Terry model, BT)：一种用于对成对比较数据进行建模的概率模型。在本文的背景下，它假设人类对两个回答 $(y_1, y_2)$ 的偏好概率 $p^*$ 可以通过一个潜在的奖励函数 $r^*$ 来建模：

  \[p^{*}(y_{1}\succ y_{2}\mid x)=\frac{\exp\left(r^{*}(x,y_{1})\right)}{\exp\left (r^{*}(x,y_{1})\right)+\exp\left(r^{*}(x,y_{2})\right)} = \sigma(r^*(x, y_1) - r^*(x, y_2))\]

  这个模型是RLHF中训练奖励模型的基础，也是DPO方法推导的起点。

• 直接偏好优化 (Direct Preference Optimization, DPO)：本文提出的核心方法。它绕过了传统的“先训练奖励模型，再用强化学习优化策略”的两阶段流程。DPO通过数学推导，直接将策略模型 $\pi_{\theta}$ 的参数与BT偏好模型联系起来，构建了一个可以直接对策略进行优化的损失函数。它本质上是将策略本身视为一个隐式的奖励模型。

相关工作

当前，为了让大型语言模型（LMs）的行为与人类意图对齐，最主流的方法是基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF）。RLHF通常遵循一个复杂的多阶段流程：

1. 监督微调（SFT）：在一个高质量的指令数据集上对预训练模型进行初步微调。
2. 奖励建模：使用一个经过SFT的模型生成多组回答，由人类标注者对这些回答进行偏好排序（例如，哪个更好）。然后，利用这些偏好数据训练一个独立的奖励模型（Reward Model, RM），该模型旨在预测人类会给特定回答打多少分。
3. 强化学习微调：将训练好的奖励模型作为环境的奖励信号，使用PPO等强化学习算法来微调SFT模型，使其生成的回答能获得更高的奖励分数。

然而，这个RLHF流程存在显著的瓶颈：

• 复杂性高：整个流程涉及训练多个模型（SFT模型、奖励模型、最终策略模型），维护成本高。
• 不稳定：强化学习阶段对超参数敏感，训练过程可能不稳定，且需要从策略模型中采样，计算开销巨大。

本文旨在解决上述问题，即寻找一种更简单、更稳定、计算成本更低的方法来直接利用人类偏好数据优化语言模型，从而替代复杂的RLHF流程。

图1: DPO直接用一个简单的分类目标来优化策略，以满足人类偏好，从而避免了强化学习的复杂性。

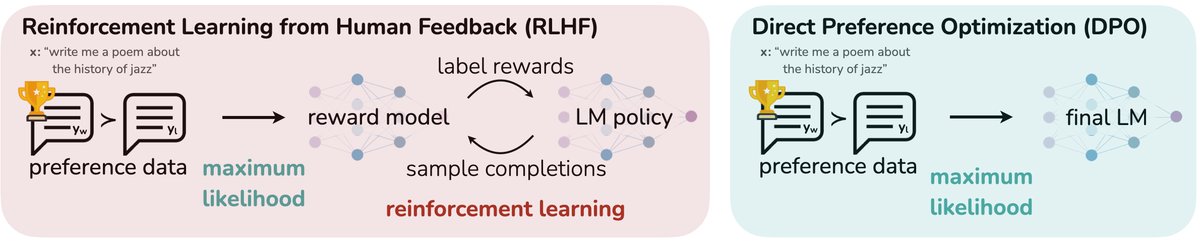
本文方法

DPO方法的核心思想是，语言模型本身就可以被看作是一个隐式的奖励模型。通过建立策略和奖励函数之间的解析关系，可以直接用偏好数据优化策略，而无需显式地拟合一个奖励模型或使用强化学习。

推导过程

DPO的推导过程优雅且直观，分为以下几步：

1. KL约束下最优策略的解析解：对于RLHF的目标函数（公式3），其最优策略 $\pi_r$ 与奖励函数 $r$ 之间存在一个确定的关系：

   \[\pi_{r}(y\mid x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y\mid x)\exp\left(\frac{1}{\beta}r(x,y)\right)\]

   其中，$Z(x)$ 是归一化因子（配分函数），确保概率和为1。这个公式表明，最优策略是在参考策略 $\pi_{\text{ref}}$ 的基础上，根据奖励函数 $r$ 的指数进行加权。

2. 反向推导奖励函数：将上述公式进行变换，可以用策略 $\pi_r$ 来表示奖励函数 $r(x,y)$：

   \[r(x,y)=\beta\log\frac{\pi_{r}(y\mid x)}{\pi_{\text{ref}}(y\mid x)}+\beta\log Z(x)\]

   这个公式揭示了本文的核心洞察：任何一个策略 $\pi_r$ 都隐含地定义了一个奖励函数（相对于参考策略 $\pi_{\text{ref}}$ 而言）。

3. 与偏好模型结合：将这个奖励函数表达式代入布拉德利-特里（BT）偏好模型。BT模型只依赖于两个回答奖励的差值 $r(x, y_w) - r(x, y_l)$。在计算差值时，与具体回答 $y$ 无关的项 $\beta\log Z(x)$ 会被抵消掉。

   因此，人类偏好概率 $p^*$ 可以直接用策略 $\pi$ 和参考策略 $\pi_{\text{ref}}$ 来表示：

   \[p^{*}(y_{w}\succ y_{l}\mid x)=\sigma\left(\beta\log\frac{\pi^{*}(y_{w}\mid x)}{\pi_{\text{ref}}(y_{w}\mid x)}-\beta\log\frac{\pi^{*}(y_{l}\mid x)}{\pi_{\text{ref}}(y_{l}\mid x)}\right)\]

4. 构建DPO损失函数：基于上述关系，可以直接为策略 $\pi_{\theta}$ 构建一个最大似然估计目标，即最小化负对数似然损失。这就得到了DPO的最终损失函数：

   \[\mathcal{L}_{\text{DPO}}(\pi_{\theta};\pi_{\text{ref}})=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D}}\left[\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w}\mid x)}{\pi_{\text{ref}}(y_{w}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{l}\mid x)}{\pi_{\text{ref}}(y_{l}\mid x)}\right)\right]\]

   这个损失函数形式上是一个简单的二元分类损失，其中logits由策略对偏好对 $(y_w, y_l)$ 的对数概率比值之差给出。

创新点

• 端到端优化：DPO将复杂的两阶段（奖励建模+RL）流程简化为单个阶段的策略优化。它直接从偏好数据中学习，无需中间的奖励模型。
• 无需强化学习：整个优化过程不涉及强化学习，避免了策略采样、价值函数估计等复杂且不稳定的步骤。训练过程就像标准的监督微调（如分类任务）一样简单稳定。
• 计算高效：由于不需要从策略模型中采样，DPO的训练成本远低于基于PPO的RLHF方法。
• 理论完备：DPO并非一个启发式方法，它在理论上精确地优化了与传统RLHF方法相同的目标函数。它通过巧妙的变量替换，找到了求解该目标的一种更直接的路径。

梯度分析

DPO损失函数的梯度直观地体现了其工作原理：

\[\nabla_{\theta}\mathcal{L}_{\text{DPO}} \propto - \bigg{[}\underbrace{\sigma( \hat{r}_{\theta}(x,y_{l})-\hat{r}_{\theta}(x,y_{w}))}_{\text{权重}}\bigg{]} \bigg{[}\underbrace{\nabla_{\theta}\log\pi(y_{w}\mid x)}_{\text{增加$y\_w$似然}} - \underbrace{\nabla_{\theta}\log\pi(y_{l}\mid x)}_{\text{降低$y\_l$似然}}\bigg{]}\]

其中，$\hat{r}_{\theta}(x,y)=\beta\log\frac{\pi_{\theta}(y\mid x)}{\pi_{\text{ref}}(y\mid x)}$ 是隐式奖励。梯度更新会增加偏好回答 $y_w$ 的概率，同时降低非偏好回答 $y_l$ 的概率。重要的是，这个更新受到一个动态权重的调节：当隐式奖励模型错误地预测偏好（即认为 $y_l$ 比 $y_w$ 更好）时，样本的权重更大，从而使模型更专注于纠正错误。这个加权机制防止了模型退化。

实验结论

本文在三个任务上评估了DPO的效果：控制情感生成、文本摘要和单轮对话。

• 优化效率极高：在控制情感生成任务中，通过绘制奖励-KL散度边界图，发现DPO在相同的KL散度下能达到比PPO高得多的奖励。DPO的效率甚至超过了能够获取真实奖励函数（而非学习的奖励模型）的PPO-GT（Oracle设置），这证明了DPO在优化RLHF目标函数方面的卓越效率。

图2 (左): DPO在所有KL值下都提供了最高的期望奖励，展示了其优化质量。

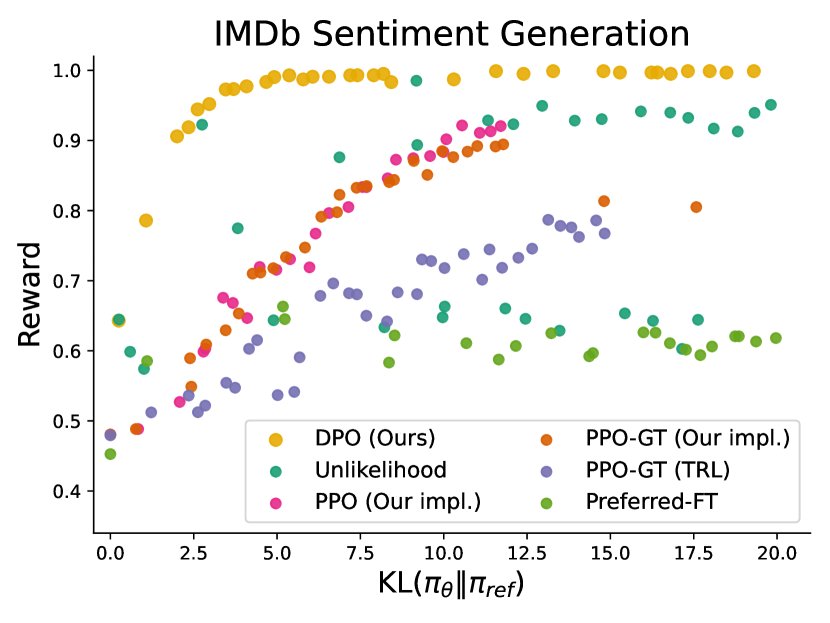
• 在标准RLHF任务上表现优异：
  • 摘要任务（TL;DR）：DPO的性能超过了PPO和Best-of-N基线，并且对采样温度的变化更加鲁棒。在与人类撰写摘要的对比中，DPO的胜率（约61%）高于PPO（约57%）。
  • 对话任务（Anthropic HH）：DPO是唯一能够显著超越数据集中“已偏好回答”的计算高效方法，其性能与计算成本高昂的Best-of-128基线相当或更好。

方法	DPO	SFT	PPO-1
人类胜率 (%)	58	43	17
GPT-4 (C) 胜率 (%)	54	32	12

表2 (节选): TL;DR摘要任务的人类与GPT-4评估对比。DPO在人类评估中显著优于PPO。

图2 (右) 和 图3 (左): 在摘要和对话任务中，DPO的性能均达到或超过了强基线。

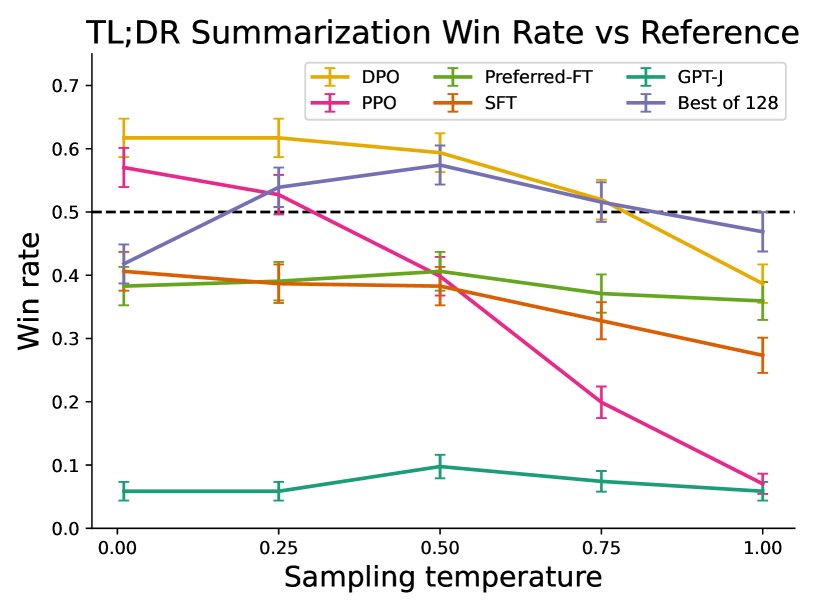
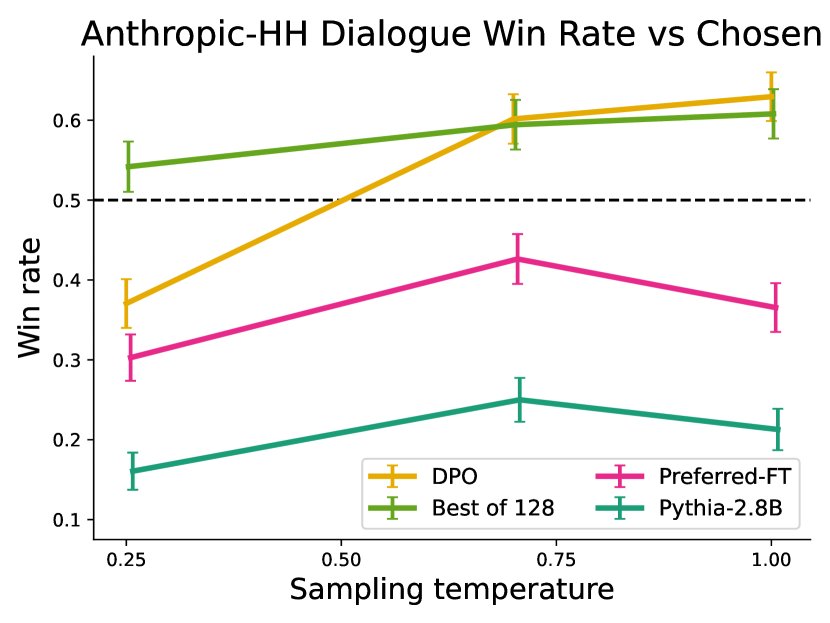
• 良好的泛化能力：将在Reddit摘要数据上训练的模型迁移到新闻文章（CNN/DailyMail）摘要任务上时，DPO的表现同样显著优于PPO，表明DPO学习到的策略具有良好的分布外泛化能力。

算法	温度 0.0	温度 0.25
DPO	0.36	0.31
PPO	0.26	0.23

表1: 在分布外的CNN/DailyMail数据集上，DPO的胜率依然高于PPO。

• 不存在显著弱点：实验结果表明，DPO在各类任务中表现稳定且优越，论文并未报告其性能不佳的场景。

最终结论：DPO是一种稳定、高效且概念简单的算法，能够与现有方法（包括基于PPO的RLHF）表现相当甚至更好，同时显著简化了从人类偏好中微调语言模型的流程。它为语言模型对齐提供了一个极具吸引力的替代方案，摆脱了传统RLHF的复杂性和不稳定性。