DRO-InstructZero: Distributionally Robust Prompt Optimization for Large Language Models

ArXiv URL: http://arxiv.org/abs/2510.15260v1
作者: Yangyang Li
发布机构: Massachusetts Institute of Technology

TL;DR

本文提出了一种名为 DRO-InstructZero 的方法，它将分布式鲁棒优化（Distributionally Robust Optimization, DRO）与贝叶斯优化（Bayesian Optimization, BO）相结合，用于搜索在数据分布发生变化时仍能保持高性能的、具有鲁棒性的语言模型指令。

关键定义

本文的核心是为指令优化引入分布鲁棒性的概念。其关键定义如下：

分布式鲁棒优化 (Distributionally Robust Optimization, DRO): 一种优化范式，其目标不是在单一、固定的数据分布上最大化期望性能，而是在一个围绕该分布构建的不确定性集合（ambiguity set）内的所有可能分布中，最大化最坏情况下的性能。这使得优化结果对分布变化更具鲁棒性。
不确定性集合 (Ambiguity Set): 以评估数据的经验分布为中心，由 f-散度（f-divergence）（如 KL 散度）定义的一个分布“球”。所有与经验分布足够“接近”的概率分布都包含在这个集合内，代表了模型在现实世界中可能遇到的各种分布扰动。
鲁棒采集规则 (Robust Acquisition Rule): 在贝叶斯优化框架中，用于选择下一个评估点的规则。与最大化期望提升（Expected Improvement, EI）或上置信界（Upper Confidence Bound, UCB）等经典采集函数不同，鲁棒采集规则旨在最大化在不确定性集合内的“最坏情况”期望效用，从而引导搜索过程明确地朝向更具鲁棒性的解。
InstructZero: 本文所基于的前人工作。该方法将指令（prompt）优化问题形式化为一个潜在空间的贝叶斯优化问题，通过一个开源语言模型生成候选指令，并由一个黑盒语言模型进行评估，从而实现指令的自动搜索。

本文方法

为了解决传统指令优化方法的脆弱性，本文提出了 DRO-InstructZero，它将分布式鲁棒优化（DRO）的思想整合到 InstructZero 的贝叶斯优化框架中。

鲁棒问题建模

传统的指令优化目标是在一个给定的数据分布 $D^t$ 上最大化期望得分：

\[\max_{v\in V}\ \mathbb{E}_{(X,Y)\sim D^{t}}\big[h(f([v;X]),Y)\big]\]

其中 $v$ 是指令，$f$ 是黑盒LLM，$h$ 是评估函数。

为了提升鲁棒性，本文将其修改为一个分布式鲁棒优化问题。首先定义一个围绕参考分布 $D^t$ 的不确定性集合 $\mathcal{U}(D^{t})$，该集合包含所有与 $D^t$ 在 f-散度（如KL散度）上距离不超过 $\epsilon$ 的分布。然后，优化目标变为最大化在最坏情况分布下的期望得分：

\[\max_{v\in V}\ \inf_{Q\in\mathcal{U}(D^{t})}\ \mathbb{E}_{(X,Y)\sim Q}\big[h(f([v;X]),Y)\big]\]

这个 minimax 结构确保了找到的指令不仅在原始分布上表现良好，在不确定性集合内的任何扰动分布下都能维持可靠的性能。

创新点：分布式鲁棒贝叶斯优化

与 InstructZero 类似，本文并不直接在离散的指令空间 $V$ 中进行搜索，而是在一个低维连续的软提示空间中进行优化。其核心创新在于将贝叶斯优化过程本身变得“鲁棒”。

高斯过程建模: 本文使用高斯过程（Gaussian Process, GP）建模的目标不再是平均得分，而是鲁棒得分 $H(p)$，即在不确定性集合内的最坏情况得分。
\[H(p)\triangleq\inf_{Q\in\mathcal{U}(D^{t})}\ \mathbb{E}_{(X,Y)\sim Q}\big[h(f([g([Ap;\text{exemplars}]);X]),Y)\big]\]
鲁棒采集函数: 这是与传统贝叶斯优化的关键区别。在每一步迭代中： a. 首先，像标准 UCB 策略一样，为候选的软提示 $p_m$ 计算一个置信上界分数 $ucb$。 b. 接着，在不确定性集合中寻找一个对抗性分布 $w_m^*$，这个分布会最小化刚刚计算出的 $ucb$ 分数。这一步是在数学上找到了当前候选提示的“最坏情况”。
\[w_{m}^{*} = \arg\min_{w' : \ \mid w' - w_{\text{ref}}\ \mid _{\mathcal{M}} \leq \epsilon(m)} \langle \mathrm{ucb}_{m}, w' \rangle\]
c. 最后，选择下一个要评估的软提示 $p_{m+1}$，使其在刚才找到的对抗性分布 $w_m^*$ 下的 $ucb$ 分数最大化。
\[p_{m+1} = \arg\max_{p} \langle \mathrm{ucb}_{m}, w_{m}^{*} \rangle\]

通过这个过程，搜索被明确地引导去寻找那些即使在最不利的分布下也能表现良好的指令，而不是仅仅追求平均表现。

算法流程

DRO-InstructZero 的完整算法流程如下。它在 InstructZero 的基础上，于每次贝叶斯优化迭代中增加了一个计算对抗性分布 $w_m^*$ 的步骤，并使用鲁棒采集规则来选择下一个候选提示。

DRO-InstructZero 算法

初始化软提示 $p_1$。
循环直到收敛或达到最大步数 $M$： a. 使用开源 LLM $g(\cdot)$ 根据当前软提示 $p_m$ 生成自然语言指令 $v_m$。 b. 使用黑盒 LLM $f(\cdot)$ 在验证集上评估指令 $v_m$，得到分数 $h_m$。 c. 将 $(p_m, v_m, h_m)$ 加入历史数据，更新高斯过程（GP）的后验均值 $\mu$ 和方差 $\sigma$。 d. 【核心步骤】： i. 定义置信上界 $ucb$。 ii. 在不确定性集合中求解，找到使 $ucb$ 最小化的对抗性权重 $w_m^*$。 iii. 选择下一个软提示 $p_{m+1}$，使其在对抗性权重 $w_m^*$ 下的 $ucb$ 值最大。 e. $m \leftarrow m+1$。
返回历史评估中得分最高的指令 $v_{i^*}$。

这一设计巧妙地将对鲁棒性的追求融入到了高效的贝叶斯搜索框架中。

实验结论

核心成果

在包含文体改写、代码调试、翻译和推理等32个BIG-Bench风格任务上的实验表明，相比于基线方法 InstructZero，DRO-InstructZero 取得了显著的性能提升。

整体性能: 在所有32个任务上，DRO-InstructZero 的平均准确率比 InstructZero 高出3.6个百分点。
分布变化下的鲁棒性: 在那些验证集和测试集表述容易发生变化的“分布漂移”任务上，DRO-InstructZero 表现尤其出色。例如，在信息性文本到正式文本的改写任务上，准确率从61.3%提升到约85-90%，绝对增益达到25-30个百分点。在领域变化的自动代码调试任务上，也获得了约25个百分点的增益。
稳定性: 在一些分布稳定的任务（如因果关系判断）上，DRO-InstructZero 同样保持了超过96%的高准确率，证明其在追求鲁棒性的同时，没有牺牲在原有分布上的性能。

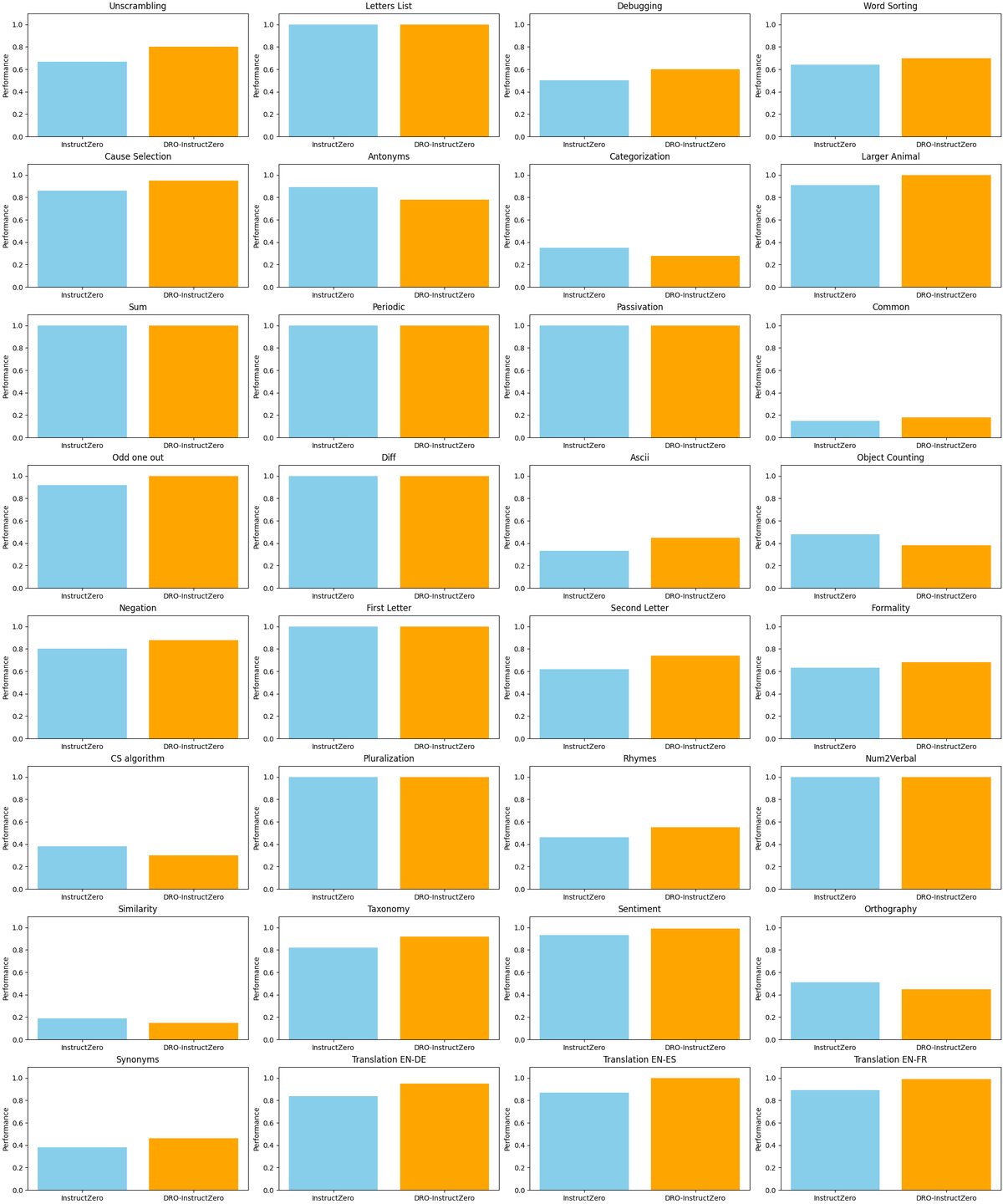
各任务准确率对比

在32个BIG-Bench任务上，DRO-InstructZero（橙色）与InstructZero（蓝色）的逐任务准确率对比

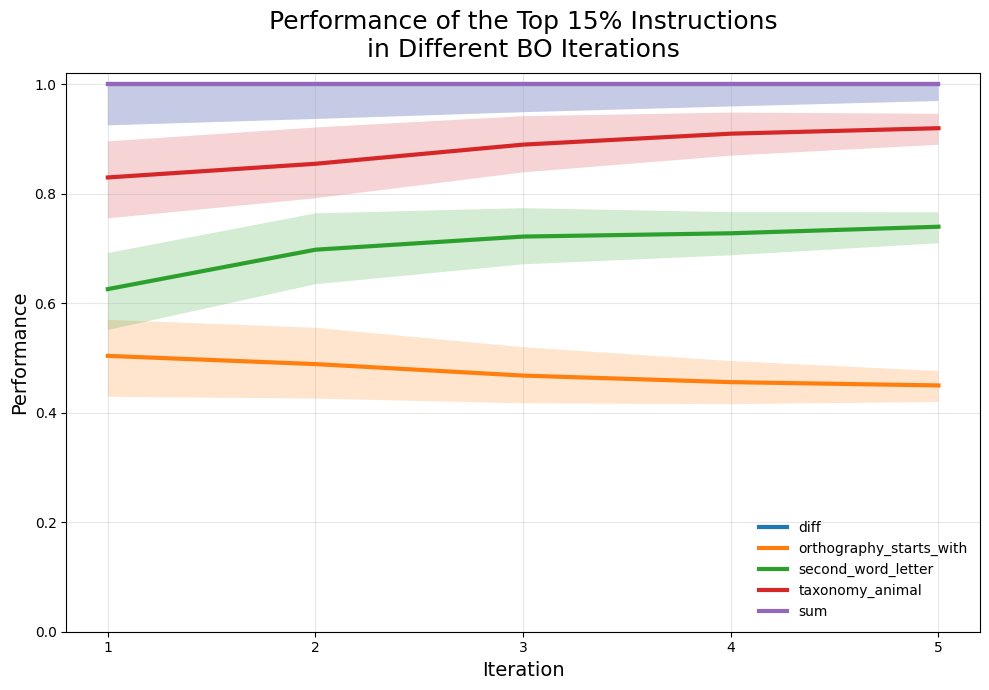
迭代过程中的性能轨迹

贝叶斯优化迭代过程中，DRO-InstructZero（橙色）与InstructZero（蓝色）的性能轨迹对比

表现不佳的场景

在少数词汇或分类任务（如同义词、对象计数等）上，本文方法出现了轻微的性能下降。这可能是因为最坏情况加权策略所强调的模式与评估器使用的精确词汇规则存在偏差。

消融实验

为了验证鲁棒性增益的确来自于本文提出的分布式鲁棒采集策略，实验对比了 InstructZero-EI (原始方法)、InstructZero-UCB (标准BO变体) 和 DRO-InstructZero。

如下表所示，DRO-InstructZero 在分布内（ID）和分布迁移（Shift）的评估中均表现最佳，尤其是在分布迁移场景下，其性能远超其他方法，证明了其优越的鲁棒性。

方法	平均准确率 (ID)	平均准确率 (Shift)
InstructZero–EI	-	61.3 ± 0.7 %
InstructZero–UCB	-	-
DRO-InstructZero (本文)	≥ 96 %	≈ 85–90 %

总结

实验结果有力地证实了本文的核心论点：通过将分布式鲁棒优化（DRO）集成到贝叶斯优化框架中，DRO-InstructZero 能够发现泛化能力更强、对分布变化更具鲁棒性的指令。这种方法在不牺牲原有分布性能的前提下，显著提升了在挑战性场景下的可靠性，为在多变的现实世界中部署大型语言模型提供了更可靠的指令对齐方案。