Dual-Weighted Reinforcement Learning for Generative Preference Modeling
-
ArXiv URL: http://arxiv.org/abs/2510.15242v1
-
作者: Han Fang; Licheng Yu; Julian Katz-Samuels; Shuang Ma; Manaal Faruqui; Karishma Mandyam; Karthik Abinav Sankararaman; Yuanhao Xiong; Hejia Zhang; Vincent Li; 等14人
-
发布机构: Carnegie Mellon University; Meta Superintelligence Labs
TL;DR
本文提出了一种名为双重加权强化学习（Dual-Weighted Reinforcement Learning, DWRL）的新框架，该框架通过一个保留了偏好建模归纳偏置的双重加权强化学习目标，将思维链（CoT）推理与Bradley-Terry（BT）模型相结合，从而在不依赖可验证奖励的通用任务上有效提升了生成式偏好模型的性能。
关键定义
本文的核心是围绕为生成式偏好模型（GPM）设计一个更优的训练框架，提出了以下关键概念：
- 生成式偏好模型 (Generative Preference Models, GPMs)：一种扩展传统标量偏好模型的方法。GPMs 不直接输出偏好分数，而是先生成一段“思考”或“评判”（即思维链），然后再基于这段思考给出最终的偏好判断（如分数或选择）。
- 对话式GPM (Dialog-based GPM)：本文提出的一种GPM实现方式。它将偏好建模重构为一个两轮对话：模型首先被要求生成对候选回答的评判（思考），然后被要求对该回答进行打分。这种设计将思考过程与打分过程解耦，便于分别进行优化。
- 双重加权强化学习 (Dual-Weighted Reinforcement Learning, DWRL)：本文提出的核心算法。它通过近似BT模型的最大似然目标，为GPM的训练引入了两个互补的权重，旨在将强化学习与偏好建模的归纳偏置结合起来。
- 实例级错位权重 (Instance-wise Misalignment Weight)：DWRL中的第一个权重。该权重在实例（即每个偏好对）级别上计算，用于强调那些模型预测与人类偏好不一致的、训练不足的样本对，其值等于模型预测错误偏好的概率。
- 群组级（自归一化）条件偏好得分 (Group-wise (Self-normalized) Conditional Preference Score)：DWRL中的第二个权重。该权重作为强化学习中的奖励信号，用于鼓励模型生成能够导出正确偏好判断的“思考”。它通过对一组采样思考的条件偏好得分进行自归一化得到。
相关工作
当前，对于具有可验证答案的任务（如数学、编程），研究者们通过从可验证奖励中进行强化学习 (Reinforcement Learning from Verifiable Rewards, RLVR) 成功地扩展了大型语言模型的思维链（Chain-of-Thought, CoT）训练。然而，将这种方法推广到答案无法自动验证的通用任务（其数据通常是成对的人类偏好）仍然是一个挑战。
这类任务通常采用Bradley-Terry (BT) 模型来学习一个偏好模型，该模型为偏好度更高的回答赋予更高的分数。受CoT的启发，近期的工作提出了生成式偏好模型 (GPMs)，让模型在打分前先生成一段评判性思考。早期的GPMs依赖于从更强模型蒸馏出的高质量思考数据进行监督训练，适用性有限。后续工作尝试将GPMs视为纯粹的生成任务，并应用RLVR进行优化，但这种方法往往会舍弃BT模型中宝贵的偏好建模归纳偏置 (preference-modeling inductive bias)，导致性能甚至不如简单的BT模型。
本文旨在解决的核心问题是：如何在不依赖外部监督思考数据的情况下，设计一个训练框架，能够有效地将CoT推理的优势与偏好建模的内在结构（归纳偏置）相结合，从而在通用偏好数据上训练出更强大的GPM。
本文方法
本文的核心方法是双重加权强化学习（DWRL），它建立在一种新颖的对话式GPM结构之上，旨在将强化学习的探索能力与传统偏好建模的结构优势结合起来。
对话式生成式偏好模型
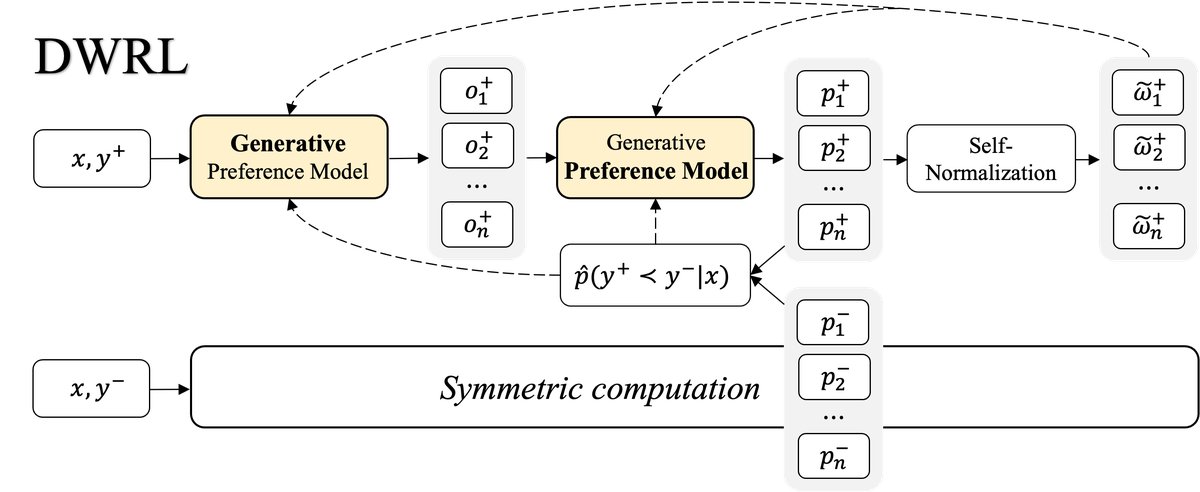
为了更好地将“思考”过程（thought generation）与“评分”过程（preference scoring）解耦，本文提出了一种对话式的GPM。其工作流程如下图所示：
- 生成思考：给定一个输入 \(x\) 和一个候选回答 \(y\)，模型首先被提示生成一段关于 \(y\) 质量的评判或思考，记为 \(o\)。
-
进行评分：随后，模型被要求基于生成的思考 \(o\) 来对 \(y\) 进行评分。具体实现上，并非让模型生成一个分数，而是计算模型在特定答案词（如对 “Is this response good? A: Yes, B: No” 问题回答 “Yes”）上的输出概率 $$p(a x,y,o)$$，这个概率被用作最终的偏好得分。
| 这种多轮对话的形式确保了思考先于评分，允许将思考 \(o\) 视为一个潜变量，并为其设计独立的优化目标。整个过程通过一次前向传播即可同时获得思考的概率 $$p(o | x,y)\(和评分的概率\)p(a | x,y,o)$$。 |
双重加权强化学习 (DWRL)
DWRL的目标是直接优化GPM在BT模型框架下的最大对数似然。对于一个偏好对 \((y+, y-)\)，其偏好概率定义为：
\[p(y^{+}\succ y^{-}\mid x)=\frac{\mathbb{E}_{o^{+}}[p(a\mid x,y^{+},o^{+})]}{\mathbb{E}_{o^{+},o^{-}}[p(a\mid x,y^{+},o^{+})+p(a\mid x,y^{-},o^{-})]}\]直接优化该目标函数非常困难，因为它涉及期望的比例，无法简单使用Jensen不等式。因此，本文通过蒙特卡洛方法直接估计损失函数 $l(\phi)=-\log p(y^{+}\succ y^{-}\mid x)$ 的梯度。
该梯度的推导形式为：
\[\nabla_{\phi}l(\phi)=-\left(\frac{p^{-}}{p^{+}+p^{-}}\right)\bigl(\nabla_{\phi}\log p^{+}-\nabla_{\phi}\log p^{-}\bigr)\]其中 $p^{+} = \mathbb{E}_{o^{+}}[p(a \mid x,y^{+},o^{+})]$，$p^{-} = \mathbb{E}_{o^{-}}[p(a \mid x,y^{-},o^{-})]$。这个梯度可以被分解为两个关键部分，从而构成了DWRL的“双重加权”机制。
权重一：实例级错位权重
梯度公式中的第一项 $\frac{p^{-}}{p^{+}+p^{-}}$ 恰好是模型预测 $y^-$ 优于 $y^+$ 的概率，即 $p(y^{+}\prec y^{-}\mid x)$。本文将其定义为 实例级错位权重 (instance-wise misalignment weight)。这个权重的作用是：当模型预测与人类偏好不一致（即错误地认为 $y^-$ 更好）时，该权重值较大，从而放大对这个“困难样本”的梯度更新，促使模型纠正错误。
权重二：群组级条件偏好得分
梯度公式中的第二项 $\nabla_{\phi}\log p^{+}-\nabla_{\phi}\log p^{-}$ 涉及对数期望的梯度，难以直接计算。通过一系列推导和蒙特卡洛近似，本文将其转化为对思考生成和评分部分分别进行优化的形式。其中，用于奖励思考生成的部分是一个自归一化的权重：
\[\tilde{\omega}_{i}=\frac{\pi_{\phi}(a\mid x,y,o_{i})}{\sum_{j=1}^{n}\pi_{\phi}(a\mid x,y,o_{j})}\]这被称为 群组级（自归一化）条件偏好得分 (group-wise (self-normalized) conditional preference score)。对于从一个候选回答 \(y\) 生成的一组思考 ${o_1, …, o_n}$，如果某个思考 $o_i$ 能够引导模型给出更高的偏好分数，那么它的权重 $\tilde{\omega}_{i}$ 就更大。这个权重作为强化学习中对思考 $o_i$ 的奖励信号，鼓励模型生成“好”的思考。
最终，DWRL的梯度估计器整合了这两个权重，同时对偏好评分和思考生成两部分进行优化。
交替更新策略
为了提高训练稳定性，DWRL采用了一种交替优化的策略：
- 优化偏好评分：固定采样的思考 \(o\)，使用加权的目标函数（Equation 14）更新模型参数，使其能更准确地打分。
- 更新权重：使用更新后的模型重新计算错位权重和条件偏好得分。
- 优化思考生成：将更新后的条件偏好得分作为优势函数（advantage），使用类似PPO的裁剪目标函数（Equation 15）来优化思考生成策略，鼓励模型产生能获得高奖励的思考。
实验结论
本文在三个偏好数据集（HH-RLHF子集、一个内部指令遵循数据集、一个数学推理数据集）和多种模型规模（Llama3和Qwen2.5）上进行了广泛实验。
| 数据集 | HH-RLHF (子集) | 指令遵循 | 数学推理 |
|---|---|---|---|
| # 训练数据 | 20,000 | 14,407 | 16,252 |
| # 测试数据 | 1,000 | 784 | 841 |
主要结果
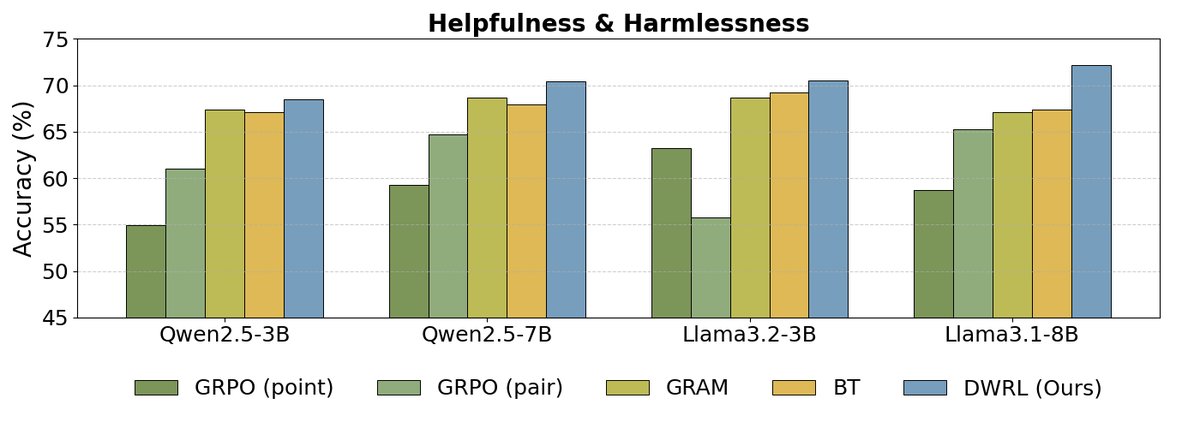
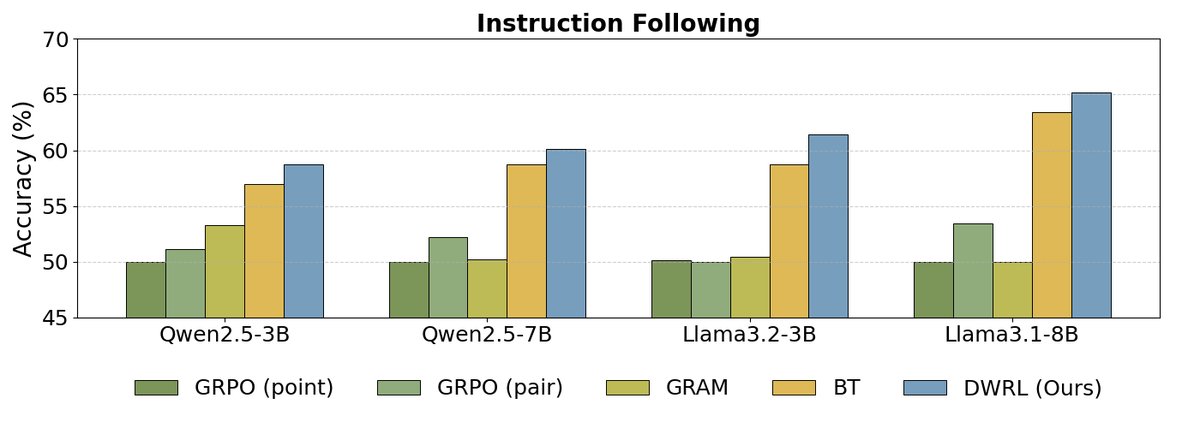
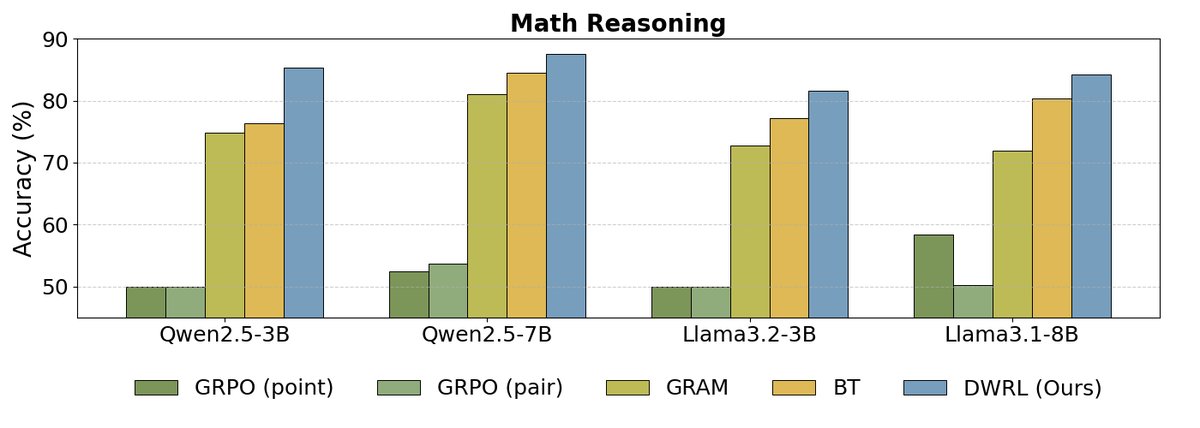如上图所示，实验结果表明：
- DWRL性能最优：在所有基准测试和模型规模上，DWRL的性能均显著优于所有基线方法，包括标准的BT模型、成对比较模型（GRAM），以及使用标准强化学习算法（GRPO）训练的GPM。在数学推理任务上，准确率提升高达9.1%。
- 标准RL方法的局限性：实验发现，直接将偏好建模视为生成任务并应用标准RL算法（如GRPO）的GPMs，其性能甚至远不如简单的BT模型。这验证了本文的核心论点：保留偏好建模的归纳偏置至关重要，简单粗暴地套用生成式RL框架是无效的。
- 成对模型（Pairwise GPM）的不足：实验还发现，将两个候选回答拼接在一起让模型判断优劣的成对模型（GRAM），在需要逐步推理的任务（如指令遵循和数学）上表现不佳，表明其泛化能力有限。
为了进一步验证，本文还与其他已发布的使用SFT（监督微调）的GPM模型（RM-R1）进行了比较。结果显示，即使经过SFT，这些模型的性能仍然远低于DWRL，这再次证明了DWRL方法的优越性。
| 模型 (Qwen2.5-7B) | HH-RLHF | 指令遵循 | 数学推理 |
|---|---|---|---|
| RM-R1 (官方) | 62.7 | 52.2 | 55.0 |
| RM-R1 (微调后) | 62.7 | 52.2 | 55.9 |
| GRPO (pair) | 64.7 | 52.2 | 53.7 |
| DWRL | 69.5 | 54.9 | 64.1 |
消融研究
消融实验进一步揭示了DWRL成功的关键因素：
- DWRL能提升思考质量：与离线生成思考再训练BT模型的方式相比，DWRL的端到端训练能够生成更具信息量的思考，从而显著提升最终的偏好判断准确率。
- 错位权重的重要性：移除实例级错位权重后，模型性能在多个数据集上出现大幅下降。这表明，该权重所代表的偏好建模归纳偏置是DWRL成功的关键组成部分。
| 模型 (Llama3.2-3B) | HH-RLHF | 指令遵循 | 数学推理 |
|---|---|---|---|
| BT (使用预填充思考) | 69.1 | 59.6 | 78.1 |
| DWRL (无错位权重) | 59.1 | 58.5 | 62.1 |
| BT (无预填充思考) | 69.2 | 58.7 | 77.2 |
| DWRL (完整版) | 70.2 | 61.3 | 81.0 |
总结
本文提出的DWRL框架成功地将CoT推理与偏好数据的内在结构相结合，为在非可验证任务上进行CoT训练提供了一条有效路径。实验证明，保留偏好建模的归纳偏置对于GPM的成功至关重要，而DWRL通过其双重加权机制巧妙地实现了这一点，从而在多个基准上取得了SOTA性能。