Dynamic Speculative Agent Planning

TL;DR

本文提出动态推测规划 (Dynamic Speculative Planning, DSP)，一个通过在线强化学习自适应调整推测步骤（speculation step）的智能体规划框架，旨在实现无损加速的同时显著降低成本，并允许用户控制延迟与成本之间的权衡。

关键定义

相关工作

当前，基于大型语言模型（LLM）的智能体在复杂任务中表现出色，但其高昂的端到端延迟严重影响了用户体验和在实时场景中的应用。现有的延迟优化方法，如减少上下文长度、步骤并行化和模仿人类双过程思维（快思考与慢思考）等，普遍存在一些关键瓶颈：

  1. 性能无法保证无损: 大多数方法为了提速会牺牲规划质量，例如依赖于额外的路由模块或复杂的提示工程，其效果不稳定。
  2. 需要预部署准备: 许多方法要求在部署前进行耗时的离线训练或模块准备，增加了实施复杂性和开销。
  3. 成本过高: 以往的推测规划方法（如ISP）采用固定的推测步骤，若设置过大，会导致大量冗余的计算和Token消耗。
  4. 缺乏用户可控性: 现有方法通常不提供让用户根据自身需求（如对延迟和成本的不同偏好）来调整系统行为的灵活性。

本文旨在解决上述问题，特别是固定推测步骤所带来的“要么加速不足，要么成本过高”的困境。其目标是创建一个无损、零准备、低成本且用户可控的智能体规划加速框架。

本文方法

为何固定推测步骤是昂贵的？

推测规划通过并行化来加速，但固定推测步骤 \(k\) 的策略存在固有矛盾：

图2：固定推测步骤的局限性

分析表明，最优的 \(k\) 值在任务执行的不同阶段是动态变化的，没有一个固定的 \(k\) 值能适应所有情况。因此，动态调整 \(k\) 值是平衡延迟与成本的关键。

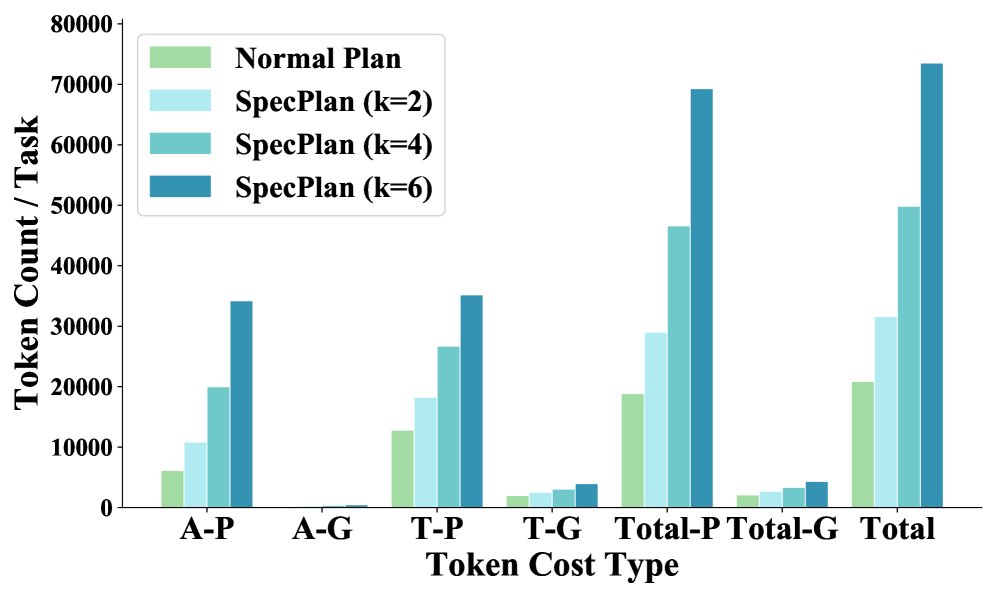
图3：不同固定k值下的Token成本分解 图3：不同固定k值下的Token成本分解 上图详细展示了在不同 \(A-T\) 组合下，随着 \(k\) 值增大，总Token成本（特别是提示Token）显著增加。

DSP框架：用在线强化学习动态预测\(k\)

本文的核心思想是：与其猜测一个固定的 \(k\)，不如在系统运行时在线学习预测它。DSP框架通过一个轻量级预测器，在每个规划片段开始时，根据当前的状态（即已有的规划轨迹）来预测接下来能成功推测的步数 \(k\)。

上图展示了DSP的工作流程：

  1. 预测: \(Predictor\)根据当前状态 \(s_i\) 预测推测步数 \(k\)。
  2. 并行执行: 近似智能体 \(A\) 和目标智能体 \(T\) 并行执行。
  3. 处理不匹配: 当 \(T\) 的验证结果与 \(A\) 的提议不符时（如 \(C\) vs \(C'\)），系统会取消后续的无效线程，并从最后一个验证正确的步骤（\(B\)）继续。
  4. 异步训练: 完成的规划片段会生成一个训练数据对（如 \((s1, k=3)\) 表示从状态\(s1\)开始成功推测了3步），一个独立的 \(Trainer\) 线程会异步地使用这些新数据来更新 \(Predictor\)，整个过程不阻塞智能体的规划。

将\(k\)值预测形式化为强化学习问题

本文将预测最优推测步数 \(k\) 的问题建模为一个马尔可夫决策过程（MDP）中的状态价值预测问题。

模型使用一个神经网络 \(V_θ(s)\) 来近似价值函数，并通过时序差分学习 (Temporal-Difference, TD learning) 进行在线更新。损失函数为：

\[L_{\theta}=\mathbb{E}_{\tau\sim\pi}[(G_{t}^{\lambda}-V_{\theta}(s_{t}))^{2}]\]

其中 \(G_t^λ\) 是 \(λ-return\)，它通过混合不同步数的回报来平衡偏差和方差。这种在线学习方式使得预测器能够实时适应任务难度的变化。

用户可控的成本-延迟权衡

DSP提供了两种机制让用户能够根据需求控制系统的行为偏好（偏向速度或偏向成本）。

  1. 有偏的\(k\)值预测 (Biased \(k\) Prediction): 在训练阶段，使用分位数回归 (Expectile Regression) 代替标准的均方误差（MSE）损失函数。

    \[L^{\tau}_{2}(u)= \mid \tau-\mathbf{1}(u<0) \mid u^{2}\]

    通过调整超参数 \(τ\) (其中 \(τ ∈ (0,1)\)):

    • \(τ > 0.5\): 模型倾向于高估 \(k\) 值，使规划更激进（更快但更贵）。
    • \(τ < 0.5\): 模型倾向于低估 \(k\) 值，使规划更保守（更慢但更省钱）。
    • \(τ = 0.5\): 无偏估计，等同于MSE。

  2. 带偏置的\(k\)值偏移 (k with Biased Offset): 在推理阶段，直接对预测出的 \(k\) 值进行调整，无需重新训练模型。

    \[k=\max(1,\hat{k}+\beta)\]

    用户可设置一个整数偏移量 \(β\)。正值 \(β\) 增加 \(k\)，负值则减少 \(k\)。

实验结论

实验在OpenAGI和TravelPlanner两个基准上进行，使用了GPT和DeepSeek系列模型作为智能体骨干。DSP与不同固定 \(k\) 值的基线进行了比较。

评估指标:

核心实验结果: 以下为OpenAGI基准测试中，使用GPT作为骨干网络的结果摘要。

表1：OpenAGI基准测试 (GPT骨干)

模式 Direct-ReAct (配置1)           CoT-MAD (配置2)          
  T(×) P(×) G(×) Cost(×) $\overline{MC}$ $\overline{K}$ T(×) P(×) G(×) Cost(×) $\overline{MC}$ $\overline{K}$
固定 (k=2) 1.00 1.00 1.00 1.00 3.00 2.00 1.00 1.00 1.00 1.00 3.00 2.00
固定 (k=4) 0.92 1.56 1.23 1.41 4.95 4.00 0.83 1.41 1.38 1.37 4.97 4.00
固定 (k=6) 0.90 2.24 1.57 1.92 6.32 6.00 0.81 1.87 1.75 1.77 6.44 6.00
Dyn. (τ=0.5) 1.01 0.87 0.91 0.88 4.33 1.78 0.98 0.95 0.95 0.95 4.44 2.10
Dyn. (τ=0.99) 0.91 1.32 1.19 1.25 5.24 3.59 0.82 1.41 1.37 1.37 5.87 4.06
Dyn. (offset=2) 0.90 1.33 1.15 1.25 5.13 3.47 0.80 1.29 1.27 1.27 5.60 3.99

表格中还包含其他\(τ\)和\(offset\)的设置以及使用DeepSeek模型和TravelPlanner基准的详细结果，趋势相似。

结论分析:

  1. DSP在降低成本的同时保持了高速: 从表中可以看出，激进的固定\(k=6\)策略虽然延迟最低（\(T(×)=0.81\)），但成本极高（\(Cost(×)=1.77\)）。而激进的DSP策略（如\(τ=0.99\)或\(offset=2\)）能够实现几乎相同的延迟（\(T(×)\)分别为0.82和0.80），但成本显著降低（\(Cost(×)\)分别为1.37和1.27），成本节省高达23%-28%。
  2. DSP能有效节省成本: 保守的DSP策略（\(τ=0.5\)）甚至可以将成本降低到基线（\(k=2\)）以下（\(Cost(×)=0.88\)），代价是轻微的延迟增加。这证明了其自适应调整、避免无效推测的能力。
  3. 用户可控性得到验证: 随着\(τ\)或\(offset\)值的增加，平均推测步数\(K\)随之上升，导致延迟\(T(×)\)下降而成本\(Cost(×)\)上升。这表明用户确实可以通过调整这些参数在延迟和成本之间进行权衡。
  4. 更低的资源占用: 相比于达到同等速度的固定\(k\)策略，DSP的平均预测步数\(K\)更低，这意味着它以更智能、更节约的方式实现了加速，对系统并发能力的压力也更小。

最终结论: 动态推测规划（DSP）框架成功地解决了固定推测步数的局限性。通过在线强化学习，它能够自适应地选择推测的激进程度，从而在不牺牲规划质量和加速效果的前提下，将总成本降低了高达30%，不必要的成本减少了60%。此外，其提供的用户控制机制，使其成为一个在多变真实世界环境中部署高效、经济的LLM智能体的强大解决方案。