Enhancing Large Language Model Reasoning with Reward Models: An Analytical Survey

• ArXiv URL: http://arxiv.org/abs/2510.01925v2

• 作者: Qiyuan Liu; Yee Whye Teh; Ning Miao; Hao Xu; Wei Chen

• 发布机构: City University of Hong Kong; Li Auto Inc.; University of Oxford

---

TL;DR

本文系统性地介绍了奖励模型（Reward Models, RMs）的基础概念、分类体系和主流应用，并深入分析了它们在提升大型语言模型（LLM）推理能力中的关键作用，最后探讨了该领域面临的核心挑战与未来方向。

引言

大型语言模型（LLM）在许多领域展现出卓越的能力，但在需要多步复杂推理的任务（如数学解题和代码生成）中仍面临挑战。早期的改进方法主要依赖于创新的提示工程或在高质量数据集上进行微调，但这些方法受限于优质推理数据的稀缺性。

最近，可验证奖励机制 (Verifiable Reward Mechanism, VRM) 显示了其潜力，它能通过单元测试或精确解等确定性规范，为模型输出提供明确的“通过/失败”反馈。然而，VRM 的局限性也很明显：它依赖于已有答案的问题，且通常只提供最终结果的稀疏反馈，无法指导中间推理过程。

因此，奖励模型（RMs）应运而生，作为真实世界评估的学习代理，为 LLM 生成的内容提供可扩展、自动化的反馈。与 VRM 不同，RM 既能应用于没有参考答案的新问题，也能评估没有确定性解的领域。本文对当代 RM 进行了系统性综述，重点关注其在增强 LLM 推理能力方面的贡献。

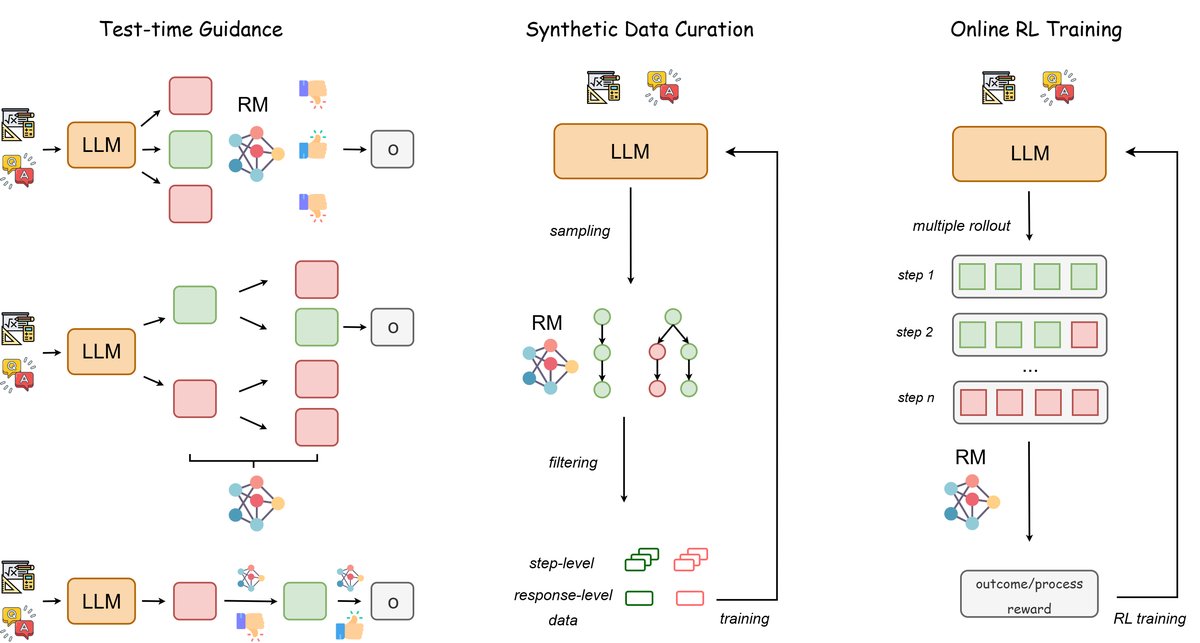
奖励模型的基础

奖励模型（RM）是一个参数化函数 \(\)R_{\theta}:\mathcal{X}\rightarrow\mathbb{R}\(\)，它将问题陈述 $p$、推理步骤 $\tau$ 等输入 $\mathcal{X}$ 映射到一个标量奖励值。RM 旨在评估 LLM 生成的推理轨迹 $\tau$ 的质量。

分类体系

本文从三个维度对奖励模型进行分类：输入粒度、奖励生成范式和输出格式。

结果奖励模型 (ORM) 与 过程奖励模型 (PRM)

根据评估的粒度，RM 可分为评估整个响应的 结果奖励模型 (Outcome Reward Models, ORM) 和评估每个独立推理步骤的 过程奖励模型 (Process Reward Models, PRM) [52]。

结果奖励模型 (ORM)

ORM 最初用于人类反馈强化学习 (RLHF)，对整个输出进行评分。它通常被构建为一个二元分类器，其输出 \(r = R_{\theta}(p, \tau) \in [0, 1]\) 表示推理过程正确的概率。训练时使用交叉熵损失：

\[\mathcal{L}_{\mathrm{ORM}}=-\mathbb{E}_{(p,\tau,\hat{y})}\bigl[\,\hat{y}\,\log r\;+\;(1-\hat{y})\,\log(1-r)\bigr].\]

其中 $\hat{y}$ 是真实标签（正确为1，错误为0）。

过程奖励模型 (PRM)

PRM 对每个推理步骤 $\tau_i$ 进行细粒度评估，输出一个步骤奖励 \(r_i = R_{\theta}(p, \tau_{1:{i-1}}, \tau_i)\)。其训练损失是所有步骤损失的总和：

\[\mathcal{L}_{\mathrm{PRM}}=-\,\mathbb{E}_{(p,\tau,\hat{y})}\Biggl[\sum_{i=1}^{n}\Bigl(\hat{y}_{i}\,\log r_{i}+(1-\hat{y}_{i})\,\log\bigl(1-r_{i}\bigr)\Bigr)\Biggr].\]

PRM 能为复杂推理提供更详细的指导，但面临标签稀缺和推理步骤定义模糊等挑战。

PRM 的数据构建与训练：

• 数据构建：PRM 的数据构建是一个关键挑战。方法包括通过蒙特卡洛树搜索（MCTS）定位首个错误步骤 (OmegaPRM [16])，或者通过自动分割策略来定义原子步骤 (ASPRM [22])。在标签标注方面，近期方法分为两类：
  • 价值模型 (Value models)：估计一个步骤导向正确最终答案的概率，常使用蒙特卡洛估计 [28, 29, 30]。
  • 奖励模型 (Reward models)：直接评估步骤本身的正确性，如标注为+1（正确）或-1（错误）[27, 31]。 一些研究如 ReasonFlux [36] 和 BiRM [37] 结合了这两种方法的优点。
• 训练方法：PRM 的训练方法也多种多样。
  • 判别式 PRM 通常作为分类器训练。方法包括多阶段训练 (Math-minos [39])、离线 Q-learning (VerifierQ [40])、时间差分学习 (TDRM [43]) 以及在无需步骤级标签的情况下隐式学习过程奖励 (ImplicitPRM [42])。
  • 生成式 PRM 则将任务视为生成问题，通过生成自然语言解释来给出奖励。方法包括利用现成模型进行评判 (LLM-as-a-judge [45])，或在特定数据上进行微调，如自然语言判断 (R-PRM [46]) 或代码验证数据 (GenPRM [47])。

判别式与生成式奖励模型

根据奖励生成范式，RM 可以分为 判别式 (Discriminative) 和 生成式 (Generative)。

• 判别式奖励模型：直接输出一个标量奖励值。
  • 显式 (Explicit) RM [53, 61] 通常在 LLM 的基础上增加一个线性头来直接输出分数。
  • 隐式 (Implicit) RM [54, 66] 则不通过监督学习，而是从模型优化前后的似然比中推导出奖励信号。例如，直接偏好优化 (DPO) 的隐式 RM 由以下公式给出：
  \[r(p,\tau_{1:{i}})=\beta\log\frac{\pi_{\theta}(\tau_{i}\mid p,\tau_{<i})}{\pi_{\mathrm{ref}}(\tau_{i}\mid p,\tau_{<i})},\]

  其中 $\pi_{\mathrm{ref}}$ 和 $\pi_{\theta}$ 分别是参考策略和优化后策略。

• 生成式奖励模型：首先生成文本形式的评价或推理过程，然后从中提取最终的数值奖励。
  • 最常见的例子是 LLM-as-a-judge [45]，它能适应多种评估任务。
  • 混合生成式 RM 是一个中间范式，它在输出标量分数的同时，还会生成文本解释以提高可解释性和鲁棒性，例如 GenRM [58] 和 CLoud [59]。

逐点与成对奖励模型

根据输出格式，RM 可分为 逐点 (Pointwise) 和 成对 (Pairwise)。

• 逐点 RM [62, 63] 为单个响应独立打分：\(\)R_{\text{pointwise}}(p, \tau) = r\(\)。
• 成对 RM [64, 78] 比较两个响应并输出更优者，这有助于学习更细微的偏好差异：\(\)R_{\text{pairwise}}(p, \tau_1, \tau_2) = \tau^*\(\)。

评测基准

为了评估不同 RM 的能力，学术界已经开发了多个基准，涵盖文本和多模态领域。

类别	领域	基准名称	主要评估内容/特点
文本RM	ORM	RewardBench [79]	首个综合性RM基准，评估聊天、推理、安全等
		RM-Bench [80]	评估对微小错误和风格偏见的敏感度
		RMB [81]	覆盖细粒度真实场景，引入 Best-of-N 评估
		PPE [82]	作为RLHF性能的低成本代理
		RAG-RewardBench [83]	评估在检索增强生成（RAG）设置下的RM
		AceMath-RewardBench [84]	专注于不同复杂度的数学问题评估
	PRM	ProcessBench [89]	任务是识别数学解题中的第一个错误步骤
		PRMBench [91]	包含更细粒度的错误类型，评估定位步骤错误的能力
		UniversalBench [90]	评估对完整推理轨迹的预测
	LLM-as-a-judge	MT-Bench [45]	评估模型在多轮对话中与人类偏好的一致性
		JETTS [92]	关注测试时任务，如重排、束搜索和批判性修正
多模态RM	ORM/PRM	VL-RewardBench [95]	挑战视觉问答、幻觉检测和复杂推理
		MJ-Bench [96]	评估作为文生图评判者的RM，覆盖对齐、安全、质量等
		Multimodal RewardBench [97]	跨六个关键领域进行综合评估
		VilBench [23]	针对视觉语言PRM，采用Best-of-N选择准确率
		VisualProcessBench [20]	使用人工标注的步骤级标签评估多模态推理正确性

奖励模型的应用：指导推理

测试时计算扩展（Test-time scaling）是一种通过在推理阶段投入更多计算资源来提升模型性能的有效方法。RM 在其中扮演了关键角色，主要通过以下三种策略增强LLM的推理能力：选择、搜索和修正。

选择

选择策略通过从一个策略模型中采样多个候选解，然后使用一个决策规则选出最终答案。

• Best-of-N (BoN) 是最流行的策略，它采样 $N$ 个解，然后选择 RM 评分最高的一个。
• 使用 ORM 进行选择：早期研究 [53, 52] 使用 ORM 对候选解进行整体评估。近期工作如 AceMath [84] 通过精心构建数据集来训练更强的 ORM。为解决 RM 可能被“欺骗”（Reward Hacking）的问题，QAlign [101] 和 Huang 等人 [102] 的工作引入了 MCMC 采样和基于不确定性的拒绝采样等方法，以获得更鲁棒的性能。
• 使用 PRM 进行选择：由于 ORM 可能忽略细节错误，后续研究转向使用 PRM 进行步骤级评分，并通过聚合函数（如最终步得分、最小步得分等）计算总分。这些方法 [27, 28, 41] 通常比 ORM 或简单的多数投票表现更好。
• 计算成本权衡：增加采样数量和提升验证器（RM）准确性都能提升性能。然而，生成更多候选解与部署一个计算成本高昂的生成式 RM 之间存在权衡。确定如何在解的生成和验证之间最优地分配计算资源是一个重要问题 [103]。

搜索

与从固定候选集中进行选择不同，测试时搜索在推理过程中动态地探索多个推理路径以构建最优解。树搜索是其中的经典框架。

• 不可逆剪枝搜索：这类方法为了效率，在每一步根据启发式评分做出决策后便不再回溯。
  • 贪心搜索 (Greedy Search) 在每一步都选择 RM 评分最高的路径。例如，GRACE [105] 和 HGS-PRM [106] 分别使用 ORM 和 PRM 在测试时进行贪心搜索。
  • 束搜索 (Beam Search) 在每一步保留多个（beam size）得分最高的候选路径，以增加找到最优解的概率。

总结与未来展望

基于现有研究和本文的分析，可以总结出关于奖励模型的几个关键发现和开放性问题：

• 模型类型的权衡：生成式 RM 通常比判别式 RM 表现更好，这可能是因为它们更好地利用了 LLM 的思维链推理能力。然而，生成式 RM 的部署和训练成本更高，使判别式 RM 在计算受限场景中更具优势。
• PRM vs. ORM：在测试时验证和排序候选解方面，PRM 因其细粒度反馈而优于 ORM。但在在线强化学习中，由于训练数据有限可能导致 PRM 信号噪声较大，其优势并不明显。
• 泛化能力：大多数 RM，特别是判别式 RM，在分布外（OOD）设置下泛化能力较差。当问题领域、难度或推理路径格式发生变化时，其性能会显著下降，这是实现通用人工智能（AGI）的关键挑战。
• 性能的共生关系：生成式 RM 的判别能力与其基础 LLM 的推理性能有很强的正相关性。这意味着提升基础模型的推理能力可以增强 RM，反之，更强大的 RM 也能通过数据生成和强化学习进一步提升 LLM 的推理能力，形成一个潜在的良性循环。
• 评估指标的局限性：当前主要关注判别准确率的 RM 评估方法，并不能充分反映其在下游任务中的实际效果。未来需要开发与真实任务性能更紧密相关的评估指标，例如 Best-of-N (BoN) 分数。