Every Question Has Its Own Value: Reinforcement Learning with Explicit Human Values

ArXiv URL: http://arxiv.org/abs/2510.20187v1
作者: Dong Yu; Haitao Mi; Kishan Panaganti; Yulai Zhao; Linfeng Song; Dian Yu
发布机构: Princeton University; Tencent AI Lab

TL;DR

本文提出 RLEV 方法，通过将可验证的正确性奖励与人类定义的显式价值（如题目分数）相结合，直接优化语言模型，使其不仅追求正确性，更优先处理高价值任务，并学会根据任务重要性调整回答的详略程度。

关键定义

本文提出或沿用了以下关键概念：

强化学习与显式人类价值 (Reinforcement Learning with Explicit Human Values, RLEV)：一种新的训练范式，它扩展了基于可验证奖励的强化学习 (RLVR) 框架。其核心思想是，将代表问题重要性的人类定义价值信号，直接整合到奖励函数中，从而使模型优化与量化的人类优先级对齐。
人类效用函数 (Human Utility Function)：一个形式化的目标函数 $U(x,y) = v(x) \cdot \mathbf{1}_{\text{correct}}(y)$，用于评估模型对提示 $x$ 的响应 $y$ 的价值。其中，$v(x)$ 是提示 $x$ 的内在价值或重要性，$\mathbf{1}_{\text{correct}}(y)$ 是一个指示函数，当响应 $y$ 正确时为 1，否则为 0。
归一化价值 (Normalized Value)：为了在不同任务间（如不同考试）创建一致的价值尺度，本文将原始分数 $s_{ij}$ （试卷 $i$ 的问题 $j$）通过除以该试卷的总分 $T_i$ 来进行归一化：$v(x) = \frac{s_{ij}}{T_i}$。这使得价值可解释为问题的“相对重要性”。
RLEV 奖励函数 (RLEV Reward Function)：为保证训练稳定性而设计的实际奖励函数。其形式为 $r(x,y) = s(x) \cdot \mathbf{1}_{\text{correct}}(y)$，其中缩放因子 $s(x) = 1 + \min(\alpha \cdot v(x), 1)$。该设计确保任何正确答案的奖励至少为 1，同时为高价值问题提供一个有上限的额外奖励，从而在激励模型的同时防止奖励过大导致训练不稳定。

本文方法

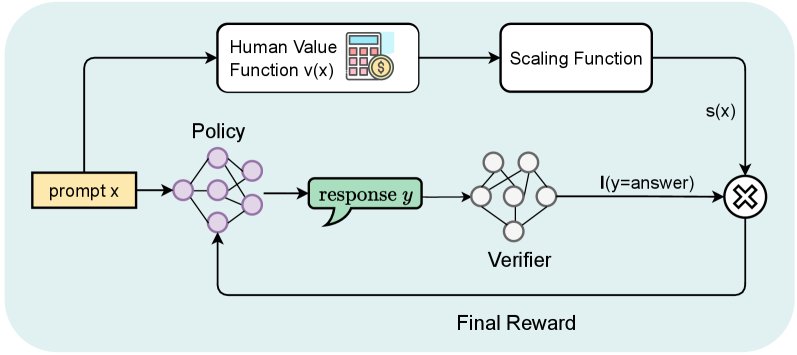
RLEV 概述。验证器可以是一个奖励模型或基于规则的函数。

方法核心

本文的核心是将人类定义的、可量化的任务价值直接融入到强化学习的奖励函数中。其出发点是一个简单而强大的原则：一个响应的效用不仅取决于其正确性，还取决于该任务本身的重要性。

本文首先定义了一个理想的人类效用函数：

\[U(x,y) = v(x) \cdot \mathbf{1}_{\text{correct}}(y)\]

其中，$v(x)$ 是提示（问题）的内在价值，$\mathbf{1}_{\text{correct}}(y)$ 判断答案是否正确。这个函数明确指出，只有正确的答案才具有价值，且其价值等于问题本身的分数。

奖励函数设计

直接使用上述效用函数 $U(x,y)$ 作为奖励信号可能导致训练不稳定，因为对于价值非常低的问题（$v(x) \approx 0$），即使回答正确，奖励也接近于零，这会抑制模型学习回答这类问题的能力。

为了解决这个问题，本文设计了一个更实用的代理奖励函数 $r(x,y)$：

\[r(x,y) = s(x) \cdot \mathbf{1}_{\text{correct}}(y)\]

其中，缩放因子 $s(x)$ 的设计是关键：

\[s(x) = 1 + \min(\alpha \cdot v(x), 1)\]

这里的 $v(x)$ 是归一化后的问题价值（分数占比），$\alpha$ 是一个超参数。

这个奖励函数的设计有两大优点：

保证基础学习信号：对于任何正确的回答，奖励至少为 1，确保模型有动力学习所有类型的问题。
提供价值激励：对于价值更高的问题，模型会获得一个额外的、最高为 1 的奖励（总奖励在 $[1, 2]$ 区间），从而激励模型优先处理高价值任务。通过 $min$ 函数进行裁剪，可以防止极端高价值问题产生过大的奖励，从而保证训练的稳定性。

梯度分析与创新点

本文的创新之处在于，通过一个简单的奖励缩放机制，显著改变了模型的学习动态。通过对策略梯度进行推导，可以揭示其工作原理。对于任意一个 token $k$ 的 logit $z_k$，其梯度可以表示为：

\[\frac{\partial J}{\partial z_{k}} = \pi(k \mid x,y_{<t})s(x) \cdot \Big(p_{k}-\sum_{v\in\mathcal{V}}\pi(v \mid x,y_{<t})p_{v}\Big)\]

其中，$p_k$ 是在当前时间步选择 token $k$ 后，最终回答正确的概率。

从这个公式可以看出，价值缩放因子 $s(x)$ 直接乘以整个梯度项。这意味着：

对于高价值问题（$s(x)$ 更大），梯度幅度会被放大。这使得模型在处理这些问题时学习得更快、更新更显著。
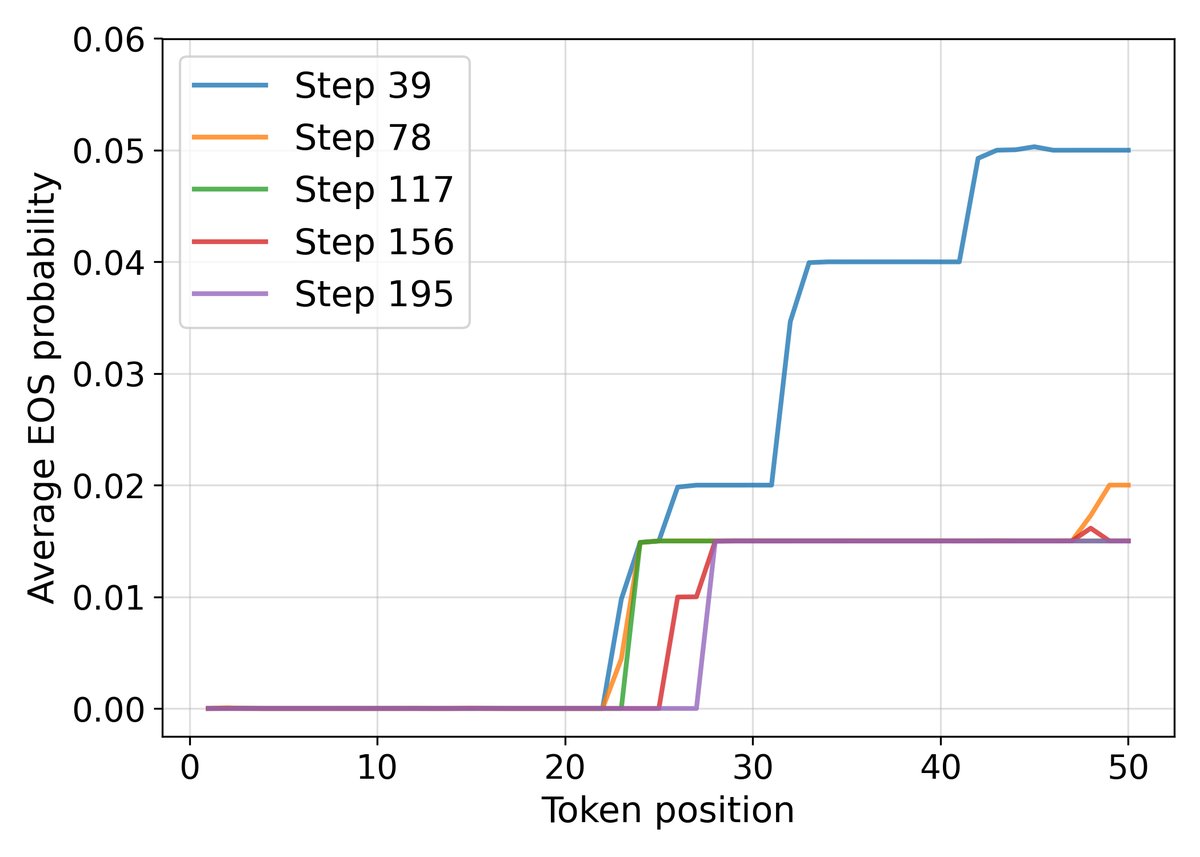
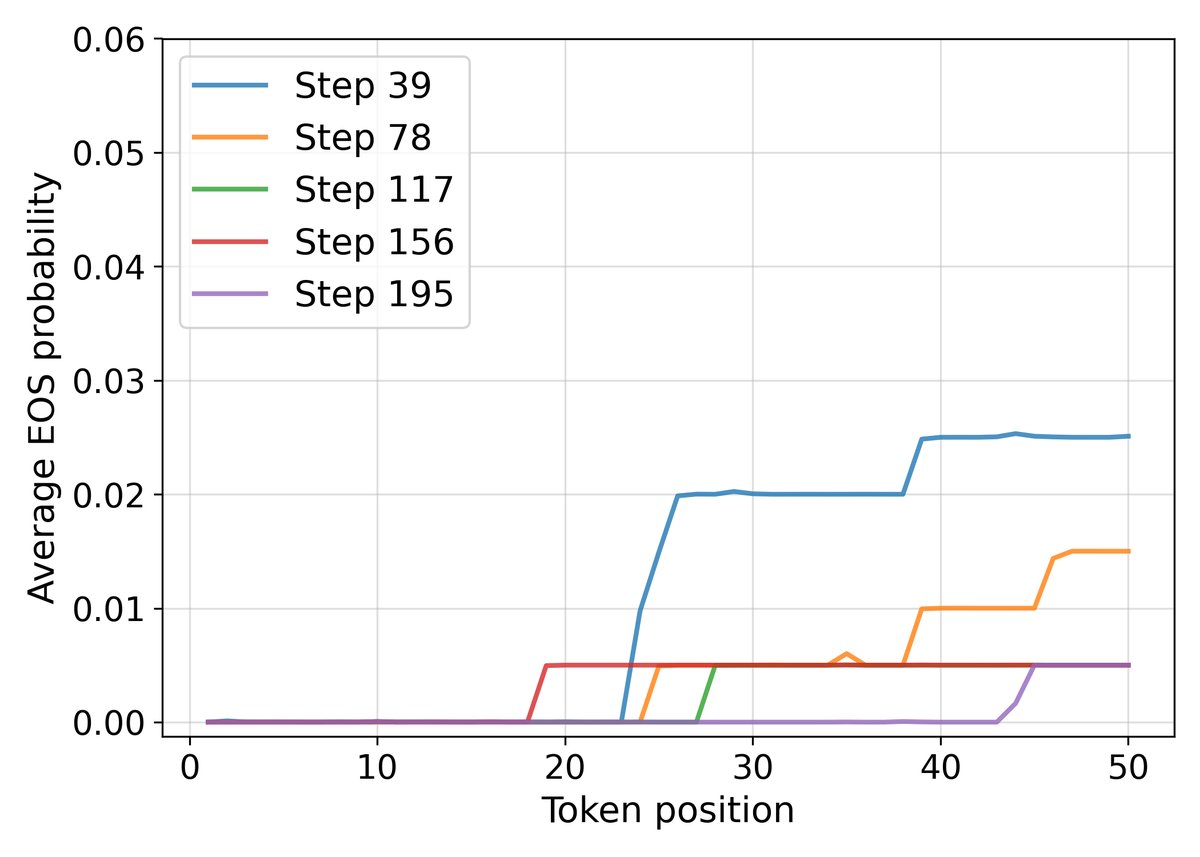
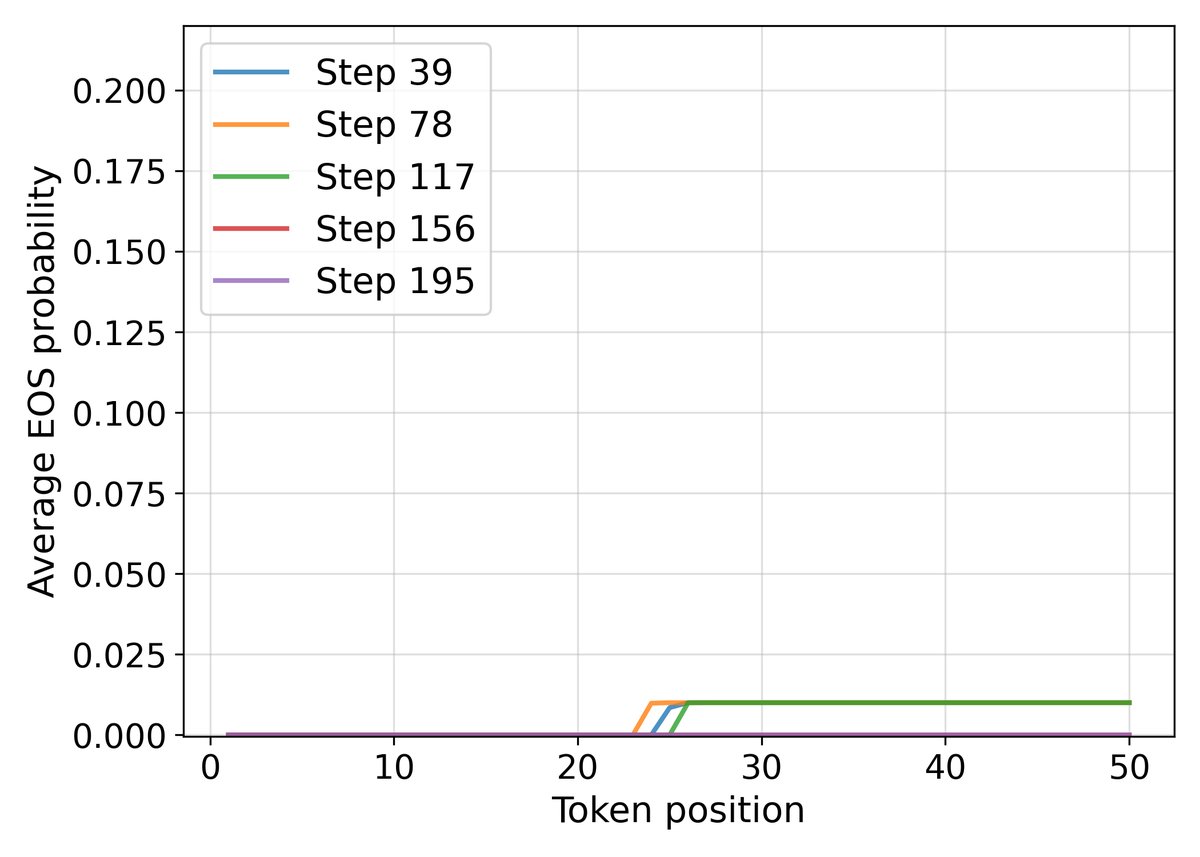
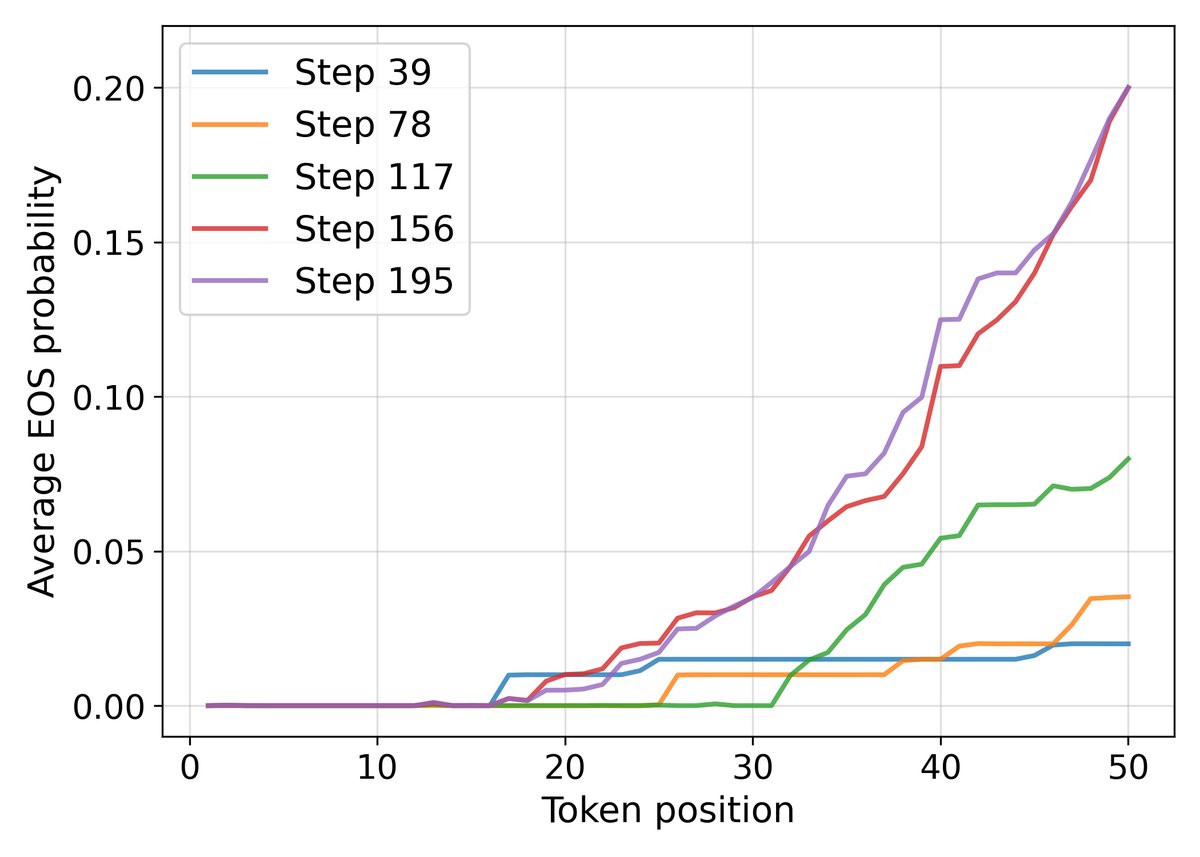
这种放大效应尤其体现在对序列结束符（End-of-Sequence, EOS）的学习上。对于 EOS 符号 $e$，其 logit 的梯度为：

\[\frac{\partial J}{\partial z_{e}} = s(x) \cdot \pi_{e}(1-\pi_{e})\big(p_{e}-\overline{p}_{\neg e}\big)\]

当提前结束序列（选择 EOS）比继续生成更有可能得到正确答案时（即 $p_e > \overline{p}_{\neg e}$），高价值问题的 $s(x)$ 会更强地推动模型学习提前终止。这解释了 RLEV 模型为何能在低价值问题上生成简洁的答案，在高价值问题上则更详尽，因为它学会了根据任务价值来动态权衡回答的详略和正确率。

实验结论

核心结果

实验结果表明，RLEV 在多个 RL 算法（REINFORCE++, RLOO, GRPO）和模型规模（7B, 32B）上均一致优于仅考虑正确性的基线方法。

算法	模型	奖励类型	准确率 (Acc)	人类对齐准确率 (H-Acc)	响应长度	价值密度
Average	7B	correctness	65.1	55.9	201.8	0.28
		RLEV	66.6 (+1.5)	57.9 (+2.0)	106.3 (-95.5)	0.55 (+0.27)
Average	32B	correctness	69.7	59.5	246.9	0.26
		RLEV	70.6 (+0.9)	62.3 (+2.8)	98.6 (-148.3)	0.63 (+0.37)

提升价值对齐准确率：RLEV 在 人类对齐准确率 (Human-Aligned Accuracy, H-Acc) 上取得了显著提升，7B 和 32B 模型平均分别提升了 2.0% 和 2.8%。这表明模型确实学会了优先答对高价值问题。
学习到价值敏感的终止策略：最引人注目的效果是，RLEV 训练的模型在响应长度上大幅缩短。例如，32B 模型的平均响应长度从 246.9 减少到 98.6。分析表明，这并非简单的“长度坍塌”，而是模型学会了在低价值问题上简洁作答，在高价值问题上保持详尽，从而实现了更高效的“价值密度”。
良好的泛化能力：尽管在中文数据上训练，RLEV 模型在多个域外（OOD）的英文和中文通用基准测试中也表现出优于基线的性能。

模型	GPQA Diamond	C-Eval	MMLU-Pro	SuperGPQA
Base-32B	33.2	84.4	57.9	33.2
+ correctness	39.9	84.9	59.9	34.0
+ RLEV	42.2 (+2.3)	85.3 (+0.4)	60.3 (+0.4)	36.0 (+2.0)

鲁棒性与消融研究

对嘈杂价值信号的鲁棒性：实验证明，即使使用不精确的“嘈杂”价值信号，如基于问题难度的弱标签或预测器生成的分数，RLEV 仍然能超越仅考虑正确性的基线。这表明该方法在现实世界中缺乏精确价值标签的场景下依然具有实用性。

方法 (RLOO)	Acc	H-Acc	响应长度	价值密度
correctness (baseline)	65.9	56.7	186.2	0.30
uniform scaling	65.3	55.1	358.4	0.15
random weights (shuffled)	66.4	57.4	280.5	0.20
RLEV (human-aligned)	66.8	58.8	86.4	0.68

价值对齐是性能提升的关键：消融研究有力地证明了性能提升来源于价值与奖励的对齐，而非简单的奖励放大。
- $uniform scaling$（所有正确答案获得相同的放大奖励）策略甚至导致性能下降。
- $random weights$（随机打乱价值标签）策略未能带来 RLEV 的核心优势（如响应长度缩短）。
- 只有当奖励的缩放与问题本身的价值明确相关时，模型才能同时提升 H-Acc 并学会高效的生成策略。

高价值问题的 EOS 概率（上）和低价值问题的 EOS 概率（下），左为基线，右为 RLEV。