Expand Neurons, Not Parameters

• ArXiv URL: http://arxiv.org/abs/2510.04500v1

• 作者: Nir Shavit; Micah Adler; Linghao Kong; Dan Alistarh; Yonadav Shavit

• 发布机构: IST Austria; MIT; OpenAI; Red Hat

---

TL;DR

本文提出了一种名为“固定参数扩展”（Fixed Parameter Expansion, FPE）的方法，通过在不增加非零参数总数的情况下增加网络中的神经元数量，来减少由特征叠加（superposition）引起的干扰，从而提升模型性能。

关键定义

• 多义性神经元 (Polysemantic Neurons)：指单个神经元同时编码多个不相关或不同概念的特征。这是导致神经网络可解释性差和性能下降的关键问题。
• 叠加假说 (Superposition Hypothesis)：一种理论，认为神经网络为了在有限的神经元数量下表示超出其容量的特征，会将多个特征“叠加”或压缩到同一个神经元中。虽然这增加了模型的表征容量，但会导致特征间的干扰。
• 固定参数扩展 (Fixed Parameter Expansion, FPE)：本文提出的核心方法。该方法将一个训练好的稠密网络重构为一个更宽的稀疏网络。具体操作是：将一个父神经元分裂成多个子神经元，并将其父神经元的输入连接（权重）不重叠地划分给这些子神经元。这样做的结果是增加了神经元的总数，但保持了网络中非零参数的总量不变。

相关工作

当前，神经网络因其复杂性和规模而常被视为“黑箱”，其内部运作机制尚不完全明了。一个核心的瓶颈是多义性神经元的存在，即单个神经元会响应多种不相关的特征。根据叠加假说，当需要表示的特征数量超过可用神经元数量时，网络会强制将多个特征的表示“叠加”在同一个神经元上。这种特征纠缠会引发相互干扰，从而降低模型的性能和可解释性。

另一方面，彩票假说 (Lottery Ticket Hypothesis, LTH) 提出，大型网络中包含着能够独立实现优异性能的稀疏子网络（“中奖彩票”）。这两种理论都揭示了网络宽度、稀疏性与可解释性之间的联系。

现有方法通常采用“训练后剪枝”或“动态增长模型”的策略。本文旨在解决由特征叠加直接导致的性能问题，提出了一条不同的路径：不改变参数总量，而是通过增加神经元数量来解耦纠缠在一起的特征，从而减少干扰。

本文方法

本文的核心是一种名为“固定参数扩展”（FPE）的后处理程序，旨在通过增加神经元的数量来缓解特征叠加问题，同时保持非零参数的总数恒定。

FPE的程序

该方法从一个预训练好的、具有单个隐藏层的全连接前馈网络开始。

1. 选择扩展因子：给定一个整数扩展因子 \(α > 1\)，将原始宽度为 \(h\) 的隐藏层扩展到新的宽度 \(h' = αh\)。
2. 分裂神经元与划分权重：对于原始网络中的每一个神经元 \(n_i\)，在新的网络中创建 \(α\) 个子神经元。然后，将父神经元 \(n_i\) 的输入权重 \(w_i\) 划分为 \(α\) 个互不相交的子集。每个子神经元继承其中一个权重子集，从而形成一个新的、更宽但稀疏的输入层权重矩阵 \(W'_1\)。这一步确保了原本共享一个父神经元的输入特征现在被分配到不同的子神经元上。
3. 调整输出层：为了匹配变宽的隐藏层，输出层的权重矩阵 \(W_2\) 也相应地被扩展。为了保持总参数量不变，会对新生成的权重矩阵 \(W'_1\) 和 \(W'_2\) 中绝对值最小的一部分权重进行剪枝。

不同参数效率范式的对比。本文提出的路径（右下）直接将一个小型稠密网络转化为一个大型稀疏网络，旨在通过增加神经元来减少特征干扰，同时保持参数数量不变。

创新点

• 解耦神经元数量与参数数量：传统方法通常将增加神经元与增加参数量等同起来。FPE的创新之处在于它打破了这种关联，允许在固定的参数预算内增加神经元的数量。
• 直击叠加问题：FPE的设计初衷就是为了解决特征叠加问题。通过将父神经元的连接分散到多个子神经元，它为原本相互竞争的特征提供了独立的计算单元，从而直接减少了特征间的干扰。
• 理论支撑：本文从理论上证明，即使是随机划分权重，FPE也能大概率保持对原有特征的覆盖，同时以 \(α^{-(2k-1)}\) 的比例减少特征冲突的概率（其中k是每个特征子句的文字数）。这说明，仅仅是增加神经元以减少“碰撞”，就能带来性能提升，而不需要精确的特征划分。

优点

该方法不仅在理论上有据可依，而且在实践中具有优势。它特别适用于现代硬件加速器，因为在这些硬件上，主要的性能瓶颈往往是移动非零参数的内存带宽，而不是原始计算量。一个更宽、更稀疏的模型可能因此更有效率。

实验结论

本文通过在符号推理任务和真实世界视觉任务上的一系列实验，验证了FPE方法的有效性。

符号推理任务（布尔可满足性问题）

在受控的布尔公式任务中，特征（子句）结构清晰，便于进行精确分析。

• 性能提升显著：与稠密的基线模型相比，FPE（特别是基于子句结构的“子句分割”策略）显著提升了任务准确率。例如，在一个8子句任务中，基线模型准确率为78.7%，而子句分割FPE模型达到了99.4%。
• 随机分割同样有效：一个关键发现是，即使是随机划分神经元权重，FPE模型（准确率88.7%）也远超基线模型。这表明性能提升的主要驱动力是减少特征在神经元上的冲突，而不仅仅是精确的特征解耦。
• 干扰度量验证：通过测量“特征容量”（Feature Capacity）和神经元权重间的“余弦相似度”，实验表明FPE确实能减少特征干扰。如下图所示，FPE模型的特征容量更高，神经元正交性更强，且这些指标的改善与模型性能的提升有很强的正相关性。

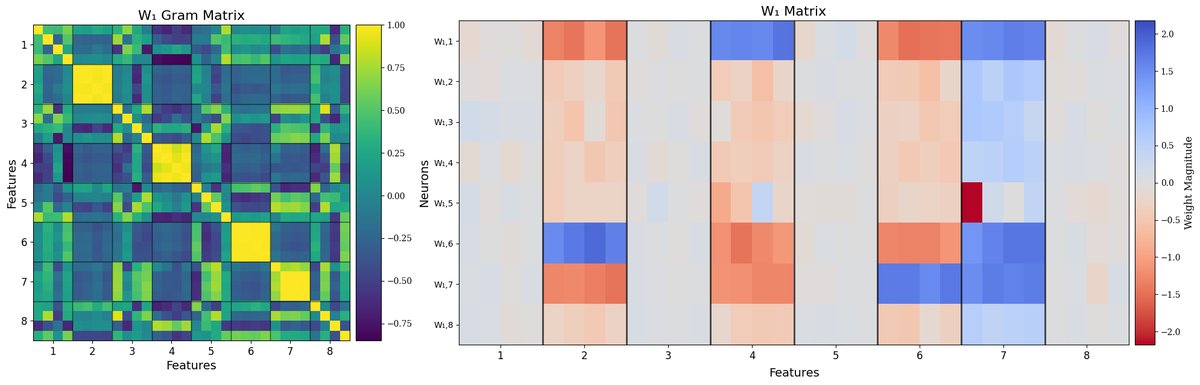稠密模型（上）与子句分割FPE模型（下）的Gram矩阵和权重矩阵。FPE模型表现出更清晰的块对角结构，表明特征解耦更好。

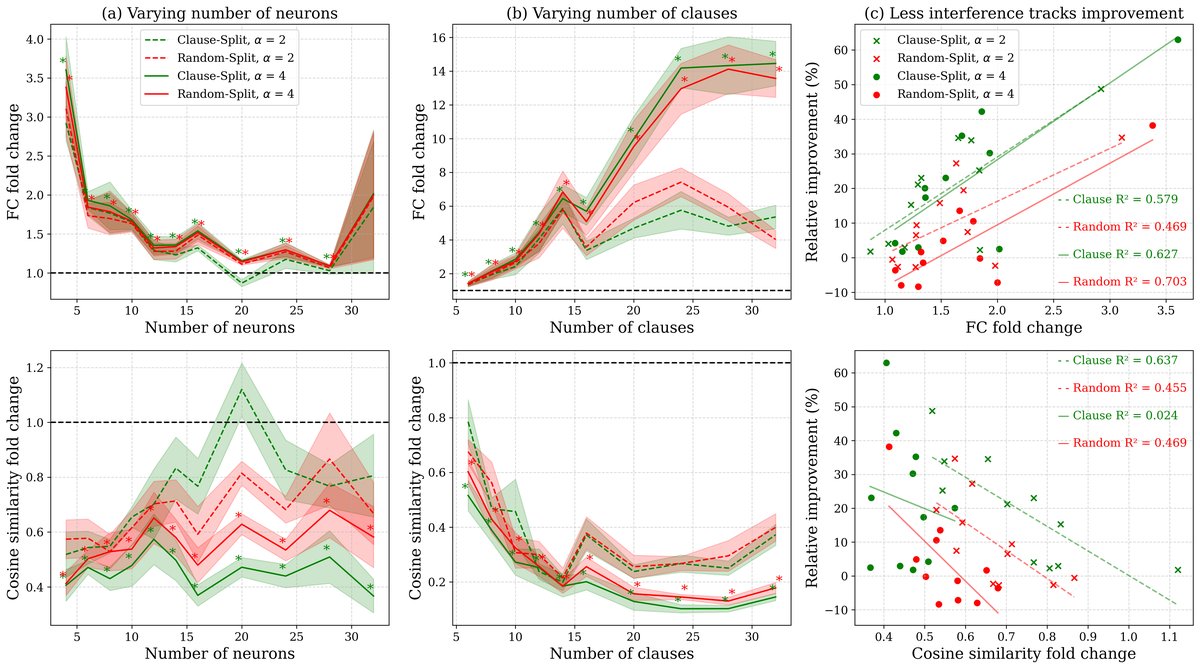特征干扰度量的变化。（a, b）图显示FPE在不同设置下均能提升特征容量、降低余弦相似度。（c）图的回归分析表明，干扰的减少与性能的提升呈强相关性。

• 叠加压力越高，收益越大：实验一致表明，当模型的表征压力（即特征数量多而神经元数量少）越大时，FPE带来的性能增益也越大。这符合叠加假说的预测。

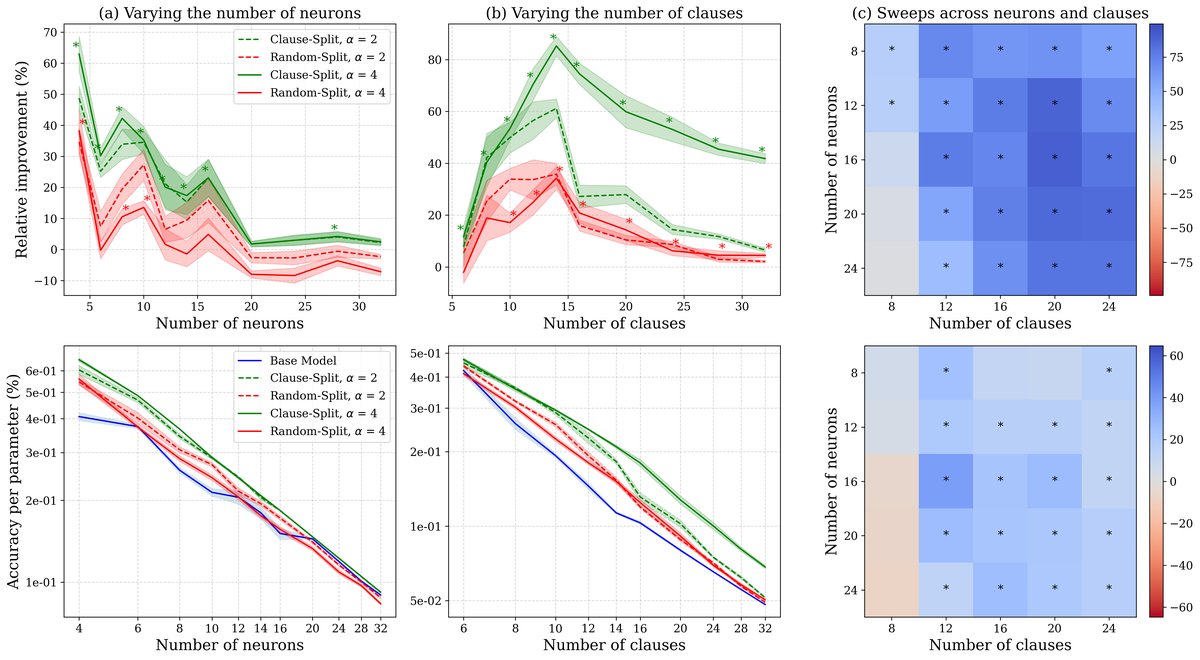不同神经元和子句数量下的性能趋势。FPE的相对性能提升在神经元较少（a）或子句较多（b）时最为明显，即叠加压力大的情况。

真实世界视觉任务

为了验证FPE的泛化能力，本文在FashionMNIST、CIFAR-100和ImageNet等数据集上进行了实验。

数据集	模型	相对准确率提升 (α=2)	相对准确率提升 (α=4)
FashionMNIST	特征分割	1.1%	1.3%
	随机分割	1.0%	1.2%
CIFAR-100	特征分割	100.2%	114.3%
	随机分割	97.4%	108.9%
ImageNet-100	特征分割	9.0%	10.3%
	随机分割	8.8%	10.5%
ImageNet-1k	特征分割	2.5%	2.9%
	随机分割	2.4%	3.0%

• 普遍有效：如上表和下图所示，FPE在所有视觉任务上都一致地优于稠密基线模型，有时甚至能将性能翻倍（如CIFAR-100）。
• 随机分割再次表现出色：在这些更复杂的任务中，基于特征聚类的分割策略与随机分割策略的表现相当。这一结果进一步强化了核心结论：增加神经元数量以创造更多的“独立空间”来分离特征，是FPE成功的根本原因，即便分割策略并非最优。

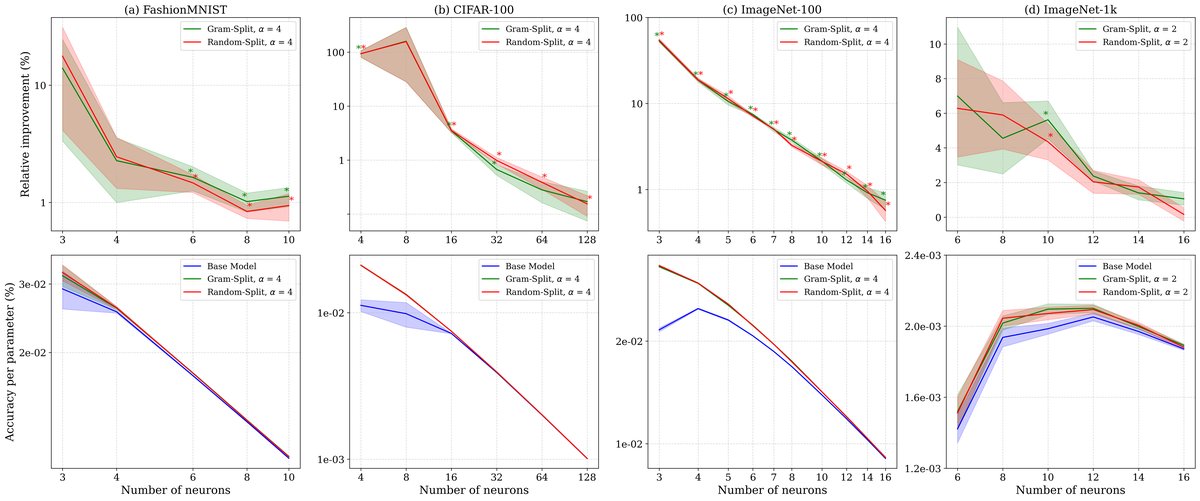FPE在真实数据集上的性能提升。无论是哪种分割策略，FPE模型在(a)FashionMNIST, (b)CIFAR-100, (c)ImageNet-100, (d)ImageNet-1k上均优于稠密基线。

总结

实验结果有力地证明，在固定的非零参数预算下，增加神经元数量是一种减少特征叠加干扰、提升模型性能的有效机制。FPE方法为在不增加模型存储成本的前提下提升模型能力提供了一条新颖且实用的途径。