Fast attention mechanisms: a tale of parallelism

• ArXiv URL: http://arxiv.org/abs/2509.09001v1

• 作者: Clayton Sanford; Jingwen Liu; Hantao Yu; Daniel Hsu; Alexandr Andoni

• 发布机构: Columbia University; Google Research

---

TL;DR

本文提出了一种名为“近似最近邻注意力”（ANNA）的高效注意力机制，其时间复杂度为亚二次方，并从理论上证明了它在保持与大规模并行计算（MPC）模型等价的强大表达能力的同时，能够高效解决关键推理任务，且其能力可涵盖低秩注意力机制。

关键定义

本文提出或沿用了以下对理解论文至关重要的核心概念：

• 大规模并行计算 (Massively Parallel Computation, MPC)：一个理论计算模型，用于描述像 MapReduce 这样的大规模分布式计算框架。该模型由多个计算机构成，这些机器在多轮（rounds）中交替进行本地计算和受限的全体通信。其关键复杂度参数包括输入大小 $N$、机器数量、每台机器的本地内存大小 $s$ 以及计算轮数 $R$。本文使用 MPC 来刻画 Transformer 的理论计算能力。

• 近似最近邻搜索 (Approximate Nearest Neighbor, ANN Search)：给定一个度量空间中的点集 $P$ 和一个查询点 $q$，ANN 搜索的目标是找到 $P$ 中任意一个点 $p$，使得其到 $q$ 的距离至多是 $q$ 的真实最近邻点距离的 $c$ 倍（其中 $c > 1$ 是近似因子）。

• 局部敏感哈希 (Locality-Sensitive Hashing, LSH)：一种用于解决高维空间中 ANN 搜索问题的核心技术。其基本思想是设计一个哈希函数族，使得空间中距离相近的点有很高的概率被映射到同一个哈希值，而距离较远的点则概率很低。

• 近似最近邻注意力 (Approximate Nearest Neighbor Attention, ANNA)：本文提出的核心注意力机制。它不是一个具体的算法，而是一族满足特定约束的注意力模型。其核心思想是，对于一个给定的查询 $q_i$，只有当键 $k_j$ 是 $q_i$ 的近似最近邻（在 $cr$ 距离内）时，注意力权重 $w_{i,j}$ 才可能大于零；而当 $k_j$ 是一个确切的近邻（在 $r$ 距离内）时，其权重 $w_{i,j}$ 必须大于一个最小阈值。这使得注意力计算变得稀疏和高效。

• 低秩注意力 (Low-rank attention)：一种主流的高效注意力机制。它通过将 $N \times N$ 的注意力矩阵 $A$ 分解为两个低秩矩阵的乘积来近似，即 $A \approx \phi_q(Q)\phi_k(K)^T$，其中 $\phi_q$ 和 $\phi_k$ 的输出维度远小于 $N$，从而将计算复杂度从 $O(N^2)$ 降低到近线性。

相关工作

标准的 Transformer 模型凭借其强大的并行信息处理能力，在深度学习领域取得了巨大成功。其表达能力已被证明与大规模并行计算（MPC）模型存在紧密联系，这意味着 Transformer 能够高效解决一大类复杂的计算任务。

然而，标准 Transformer 的一个核心瓶颈是其注意力机制的二次方时间复杂度 ($O(N^2)$，其中 $N$ 是序列长度)，这严重限制了其在处理长序列时的可扩展性。虽然已有很多工作提出了亚二次方复杂度的替代方案，如低秩近似或基于最近邻搜索的方法，但这些高效方法是否能保持标准注意力的强大表达能力，在理论上尚不明确。

本文旨在解决这一核心问题：是否存在一种计算上高效（亚二次方时间）的注意力机制，它不仅能够保持标准注意力强大的理论表达能力，还能更紧密地与 MPC 模型的计算能力对等？

本文方法

本文的核心是提出并分析了一种名为“近似最近邻注意力”（ANNA）的新型高效注意力机制。

ANNA 的核心思想与定义

ANNA 的核心思想是将注意力计算从“全局所有 token 交互”转变为“局部邻近 token 交互”。它借鉴了近似最近邻（ANN）搜索的理念，规定一个查询（query）只与其在嵌入空间中的“邻居”键（key）进行交互。

形式上，一个注意力单元被称为 ANNA，如果它对于给定的半径 $r$、近似因子 $c > 1$、分布因子 $\ell \ge 1$ 和失败概率 $\eta \in [0, 1)$ 满足以下两个条件：

1. 稀疏性约束：只有当键 $k_j$ 位于查询 $q_i$ 的 $cr$ 邻域内时，注意力权重 $w_{i,j}$ 才可能为正。

   \[w_{i,j} > 0 \Rightarrow k_j \in \mathcal{N}(q_i, cr)\]

2. 重要性约束：当键 $k_j$ 位于查询 $q_i$ 的 $r$ 邻域内时，其获得的注意力权重必须不低于一个下限。

   \[k_j \in \mathcal{N}(q_i, r) \Rightarrow w_{i,j} \ge \frac{1}{( \mid \mathcal{N}(q_i,cr) \mid -1)\ell+1}\]

这个定义描述了一个模型家族，而不是一个单一的实现。

基于 LSH 的高效实现

为了让 ANNA 能够高效计算，本文提出了一种基于局部敏感哈希（LSH）的具体实现算法。该算法的运行时间为亚二次方，从而解决了标准注意力的效率瓶颈。 算法流程如下：

1. 预处理（Hashing）：创建 $\ell$ 个哈希表。对于每一个键值对 $(k_j, v_j)$，使用 $\ell$ 组不同的哈希函数将其哈希到每个哈希表对应的桶（bucket）中。每个桶累加落入其中的所有值向量 $v$ 和对应的计数。
2. 查询（Querying）：对于每一个查询 $q_i$，使用相同的哈希函数找到它在 $\ell$ 个哈希表中对应的桶。
3. 聚合（Aggregation）：将从这 $\ell$ 个桶中检索到的所有值向量求和，并除以总计数，得到最终的注意力输出。这个过程等效于对与查询 $q_i$ 哈希冲突的键的值向量进行加权平均。

该 LSH 实现保证了 ANNA 的定义，并且其总运行时间为 $O(mN^{1+3\rho}\log N)$，其中 $\rho$ 可以通过调整 LSH 参数变得很小，从而实现近线性的时间复杂度。

创新点与优点

• 创新点：本文的根本创新在于，它不仅提出了一种高效的注意力机制，更重要的是通过与 MPC 计算模型建立等价关系，从理论上严格证明了其表达能力。这为评估和理解各种高效注意力机制提供了一个统一的理论框架。

• 优点：

  1. 高效性与表达能力的统一：ANNA-Transformer 在实现亚二次方复杂度的同时，保留了标准 Transformer 模拟 MPC 算法的能力，解决了效率和性能之间的权衡。本文证明了 ANNA-Transformer 和 MPC 模型之间存在一个更紧密的双向模拟关系，相比标准 Transformer，所需的机器数量从 $O(N^2)$ 降低到近乎线性的 $O(N^{1+3\rho})$。
  2. 更强的模型表达力：本文证明了常数层 ANNA-Transformer 能够模拟常数层低秩 Transformer。这意味着在同等高效的条件下，ANNA 的表达能力不弱于、甚至可能强于低秩注意力。例如，对于 $k$-hop 推理任务，ANNA-Transformer 可以在 $O(\log k)$ 的深度内解决，而低秩注意力需要 $\Omega(k)$ 的深度。
  3. 坚实的理论基础：通过将 ANNA-Transformer 与 MPC 关联，可以直接将 MPC 领域的复杂度下界转化为 ANNA-Transformer 的深度下界，从而为其能力边界提供了理论依据。

实验结论

理论任务验证

本文通过理论构建和实证实验，在两个关键的基准推理任务上验证了 ANNA-Transformer 的能力：

• Match2：一个衡量模型关联配对元素能力的任务。理论分析表明，单层 ANNA 注意力机制即可解决此问题。
• $k$-hop Induction Heads：一个泛化的“上下文学习”任务，要求模型进行多步关联推理。理论分析表明，ANTA-Transformer 可以在 $O(\log k)$ 的深度和亚线性的宽度下解决此任务，这远优于需要 $\Omega(k)$ 深度的低秩注意力模型和循环网络。

实验结果

由于本文提出的 LSH 实现是不可微的，实验采用了一种“蒸馏”策略：首先训练一个可微的、带有归一化和温度参数的 Softmax 注意力模型作为代理，然后将其权重迁移到 ANNA-Transformer 中进行评估。

• Match2 任务：在序列长度 $N=32$ 的设定下，单层 ANNA-Transformer（使用 8 个哈希表）能够达到零错误率，成功解决了该任务。
• Induction Heads 任务 ($k=1$)：在序列长度 $N=100$ 的设定下，两层 ANNA-Transformer（使用 32 个哈希表）能够达到低至 $0.1$ 的错误率，表现优异。

实验结果图直观展示了模型性能随哈希表数量的变化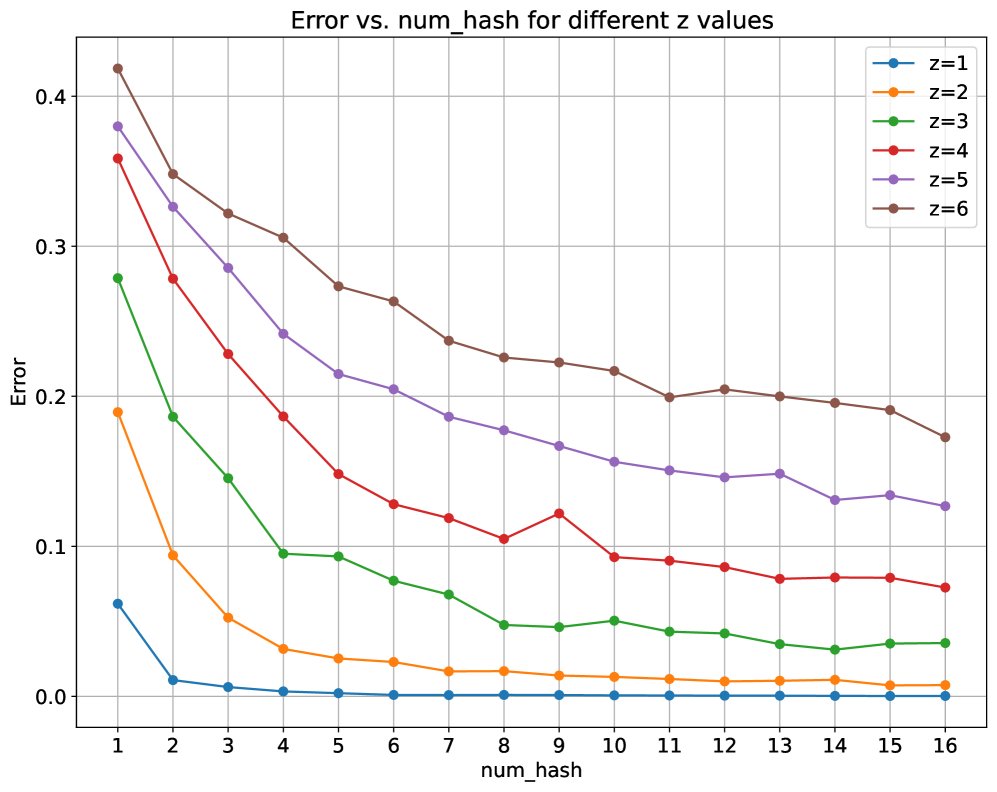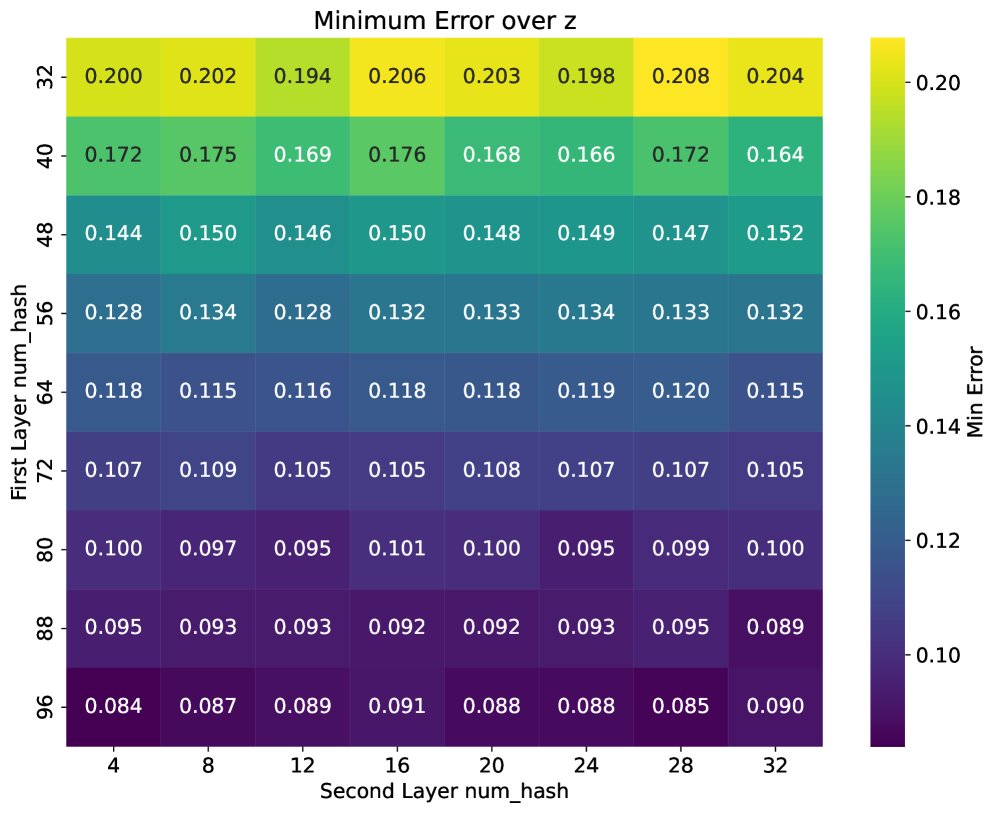： 左图为 Match2 任务的错误率，右图为 Induction Heads 任务的错误率。可以看出，随着哈希表数量 $\ell$ 的增加，模型错误率显著下降。

总结

实验结果为理论分析提供了实证支持，证明了 ANNA-Transformer 不仅在理论上强大，在实践中也能够被有效训练（通过代理模型）来解决复杂的推理任务。这表明 ANNA 是一种兼具高效率和强表达能力的有前途的注意力变体。本文最终结论是，ANNA-Transformer 在保持标准 Transformer 核心计算能力的同时，提供了一条通向更长序列、更高效模型的路径。