FlowRL: Matching Reward Distributions for LLM Reasoning

• ArXiv URL: http://arxiv.org/abs/2509.15207v1

• 作者: Ning Ding; Dinghuai Zhang; Kaiyan Zhang; Lin Chen; Bo Xue; Zhouhan Lin; Qizheng Zhang; Zhenjie Yang; Che Jiang; Bowen Zhou; 等22人

• 发布机构: Microsoft Research; Peking University; Renmin University of China; Shanghai AI Laboratory; Shanghai Jiao Tong University; Stanford University; Toyota Technological Institute at Chicago; Tsinghua University

---

TL;DR

本文提出了一种名为 FlowRL 的强化学习算法，它通过匹配完整的奖励分布而非简单地最大化奖励，来提升大型语言模型（LLM）的推理能力，从而解决了现有方法容易陷入模式崩溃、探索多样性不足的问题。

关键定义

本文的核心是围绕将传统的奖励最大化范式转变为奖励分布匹配范式，关键概念如下：

• FlowRL: 本文提出的核心算法。它是一种策略优化算法，其目标不是像传统强化学习那样找到单一的最优解，而是让模型的输出分布与奖励信号引导的目标分布相匹配。这通过一种受流网络（GFlowNets）启发的流平衡（flow balancing）机制实现，鼓励智能体探索更多样化且有效的推理路径。

• 奖励分布匹配 (Reward Distribution Matching): 本文的核心理念。与最大化标量奖励值的传统方法不同，该方法旨在学习一个策略 $$π_θ(y

  x)\(，使其输出的概率与奖励值\)r(x,y)\(的指数成正比，即\)π_θ(y

  x) ∝ exp(β * r(x,y))$$。这能有效避免策略过分集中于少数几个高奖励的“主模式”，从而提升生成解决方案的多样性。

• 轨迹平衡 (Trajectory Balance): 源自 GFlowNets 的一个核心概念，被本文用作实现奖励分布匹配的可行优化目标。它将复杂的反向KL散度最小化问题，转化为一个更稳定的均方误差损失函数：$$ (log Z_φ(x) + log π_θ(y

  x) - βr(x,y))^2 \(。通过最小化该损失，可以同时学习策略\)π_θ\(和用于归一化的配分函数\)Z_φ$$。

• 可学习的配分函数 (Learnable Partition Function, \(Z_φ(x)\)): 借鉴了能量基模型的思想，本文引入一个可学习的函数 \(Z_φ(x)\)，用于将标量奖励 \(r(x,y)\) 归一化为一个合法的概率分布。这使得在不知道整个解空间的情况下，也能构建一个有效的目标分布进行匹配。

相关工作

当前，应用于大型语言模型推理任务的强化学习（RL）方法，如 REINFORCE、PPO 和 GRPO，已取得显著成功。这些方法构成了该领域的主流技术（SOTA）。

然而，这些方法共同的根本目标是奖励最大化 (reward-maximizing)。这一目标导致了一个关键瓶颈：模式崩溃 (mode collapse)。具体来说，模型倾向于过度优化那些最常见或最容易获得高分的推理路径（即奖励分布的主导模式），而忽略了其他同样有效但出现频率较低的解法。这种现象极大地限制了生成推理路径的多样性，并损害了模型在面对新问题时的泛化能力。

因此，本文旨在解决的核心问题是：如何在强化学习训练中促进智能体的多样化探索，以防止其过早收敛到少数几个占主导地位的解决方案模式，从而提升模型的泛化推理能力。

本文方法

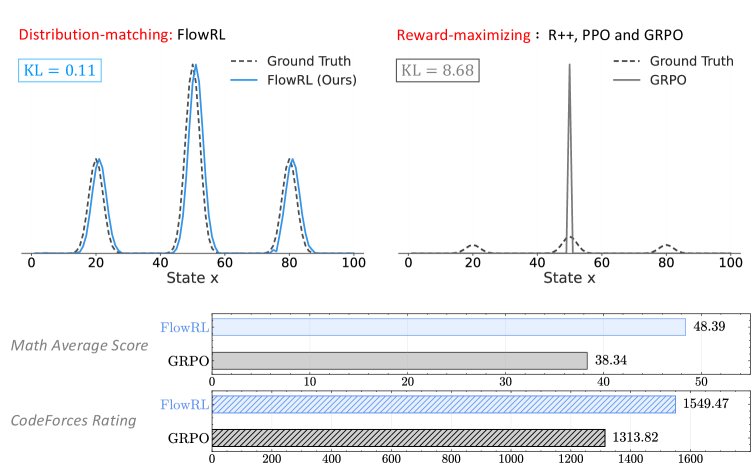
本文方法的核心是将优化目标从传统的奖励最大化转变为奖励分布匹配。

从奖励最大化到分布匹配

传统RL方法如PPO和GRPO因追求最高奖励而易陷入模式崩溃。为解决此问题，本文提出将策略 \(π_θ\) 的输出分布与一个由奖励定义的目标分布对齐。这通过最小化策略分布与目标分布之间的反向KL散度 (reverse KL divergence) 来实现。

由于奖励 \(r(x,y)\) 是一个标量，无法直接构成概率分布，本文引入一个可学习的配分函数 (partition function) \(Z_φ(x)\) 来进行归一化，从而构建出目标分布 $$~π(y

x) = exp(βr(x,y)) / Z_φ(x)$$。优化目标形式化为：

\[\min\_{\theta}\mathcal{D}\_{\mathrm{KL}}\left(\pi\_{\theta}(\mathbf{y}\mid\mathbf{x})\,\middle\ \mid \,\frac{\exp(\beta r(\mathbf{x},\mathbf{y}))}{Z\_{\phi}(\mathbf{x})}\right)\quad\Rightarrow\quad\pi\_{\theta}(\mathbf{y}\mid\mathbf{x})\propto\exp(\beta r(\mathbf{x},\mathbf{y}))\]

这个目标鼓励策略按奖励高低成比例地采样所有高奖励轨迹，而不仅仅是奖励最高的轨迹。

直接优化上述KL散度是困难的。本文证明（命题3.1），该KL散度最小化问题等价于最小化一个轨迹平衡 (Trajectory Balance) 损失：

\[\min_{\theta}\left(\log Z_{\phi}(\mathbf{x})+\log\pi_{\theta}(\mathbf{y}\mid\mathbf{x})-\beta r(\mathbf{x},\mathbf{y})\right)^{2}\]

这个均方误差形式的目标更易于优化，并可直接集成到现有的RL框架中。

FlowRL算法

尽管轨迹平衡目标在理论上很优雅，但直接应用于长达数千token的思维链（CoT）推理时会遇到两个关键挑战：

1. 问题 I：长轨迹导致的梯度爆炸。 轨迹平衡是序列级别的目标，\(logπ_θ(y|x)\) 项是所有token的对数概率之和。对于长序列，该项的梯度会随序列长度线性增长，导致训练不稳定。

2. 问题 II：采样不匹配。 轨迹平衡目标理论上要求从当前策略 \(π_θ\) 中进行在线（on-policy）采样，而PPO等高效算法通常使用从旧策略 \(π_θ_old\) 中采集的离线（off-policy）数据，存在分布不匹配问题。

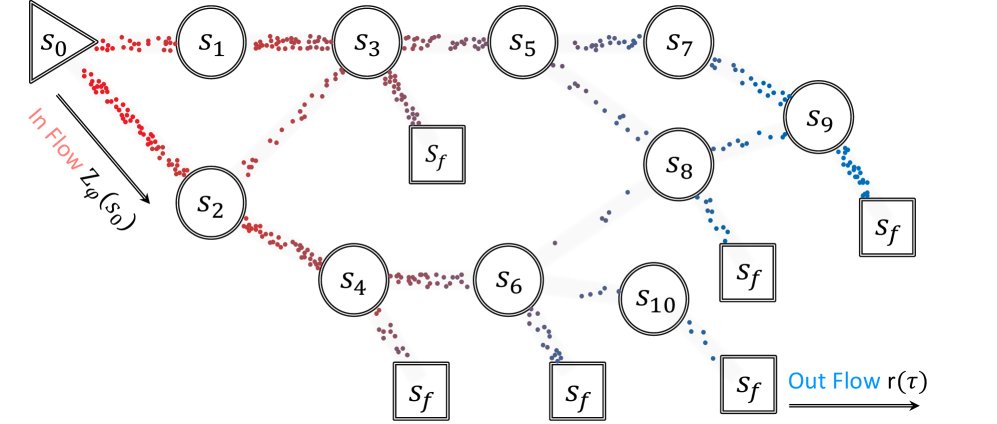
为解决上述问题，本文提出了FlowRL算法，其最终的优化目标在轨迹平衡的基础上集成了以下改进：

• 引入参考模型：为了更好地约束奖励分布，目标奖励中加入了参考模型 \(π_ref\) 作为先验，形式为 $$exp(βr(x,y)) * π_ref(y

  x)$$。

• 长度归一化 (Length Normalization)：为解决梯度爆炸问题，将序列对数概率项 $$logπ_θ(y

  x)\(除以其长度\)

  y

  $$。这平衡了长短序列对梯度的贡献，稳定了训练信号。

• 重要性采样 (Importance Sampling)：为修正采样不匹配问题，引入了PPO风格的重要性权重 $$w = π_θ(y

  x) / π_old(y

  x)$$ 来对损失进行加权。为保证稳定，计算权重时对当前策略的梯度进行分离（detach），并对权重进行裁剪。

综合以上改进，FlowRL的最终损失函数为：

\[\mathcal{L}\_{\text{FlowRL}}(\theta) = \mathbb{E}\_{\mathbf{y}\sim\pi\_{\text{old}}}\left[w\cdot\left(\log Z\_{\phi}(\mathbf{x})+\frac{1}{ \mid \mathbf{y} \mid }(\log\pi\_{\theta}(\mathbf{y}\mid\mathbf{x})-\log\pi\_{\mathrm{ref}}(\mathbf{y}\mid\mathbf{x}))-\beta\hat{r}(\mathbf{x},\mathbf{y})\right)^{2}\right]\]

其中，裁剪后的重要性权重 \(w\) 和归一化奖励 \(r̂\) 定义为：

\[w=\text{clip}\left(\frac{\pi\_{\theta}(\mathbf{y}\mid\mathbf{x})}{\pi\_{\text{old}}(\mathbf{y}\mid\mathbf{x})},1-\epsilon,1+\epsilon\right)^{\text{detach}},\quad\hat{r}\_{i} =\frac{r\_{i}-\mathrm{mean}(\mathbf{r})}{\mathrm{std}(\mathbf{r})}\]

通过这个精心设计的优化目标，FlowRL成功地将分布匹配的思想应用于长序列生成任务，同时保持了训练的效率和稳定性。

实验结论

主要结果

实验在数学和代码推理两大领域展开，使用了7B和32B参数规模的模型。结果表明，FlowRL在各个基准上均一致且显著地优于所有基于奖励最大化的基线方法（REINFORCE++, PPO, GRPO）。

数学推理：如下表所示，在32B模型上，FlowRL的平均准确率达到了48.4%，相比PPO和GRPO分别提升了5.1%和10.1%。在MATH-500和Olympiad等高难度基准上表现尤其出色。

方法	模型	AIME’24/25	AMC’23	MATH-500	Minerva	Olympiad	平均
R++	7B	20.37	53.69	24.32	34.18	7.92	28.10
PPO	7B	25.00	54.49	28.57	42.45	11.23	32.35
GRPO	7B	25.00	56.40	30.15	40.54	11.39	32.70
FlowRL	7B	28.75	58.60	31.33	45.45	14.07	35.63
R++	32B	30.00	73.10	38.65	45.42	16.58	40.75
PPO	32B	31.87	78.80	37.15	50.11	18.00	43.19
GRPO	32B	32.50	78.50	37.00	49.33	17.56	42.98
FlowRL	32B	36.25	83.10	42.22	59.33	21.11	48.40

代码推理：如下表所示，FlowRL在LiveCodeBench、CodeForces和HumanEval+三个 challenging 的代码基准上也全面超越了基线方法，展示了其强大的泛化能力。

方法	LiveCodeBench	CodeForces (Rating / Percentile)	HumanEval+
R++	35.03	1297.0 / 64.9	80.59
PPO	35.83	1480.9 / 79.5	82.52
GRPO	36.33	1515.2 / 81.3	82.72
FlowRL	37.43	1549.5 / 83.3	83.28

消融实验

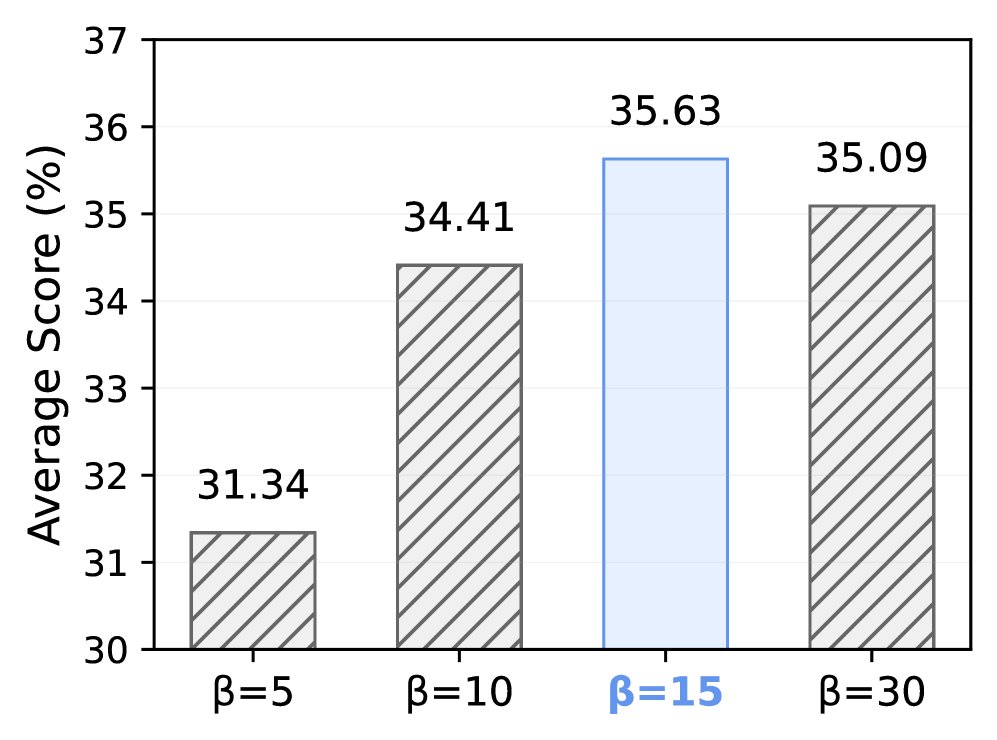
消融实验验证了FlowRL设计的有效性。

• 重要性采样：移除重要性采样会导致性能大幅下降（平均准确率从35.63%降至26.71%），证明了该模块对于修正离线采样带来的分布不匹配问题至关重要。
• 超参数\(β\)：对 \(β\) 的研究表明，\(β=15\) 时模型表现最佳，该参数控制了奖励信号在目标分布中的权重。

分析

多样性分析

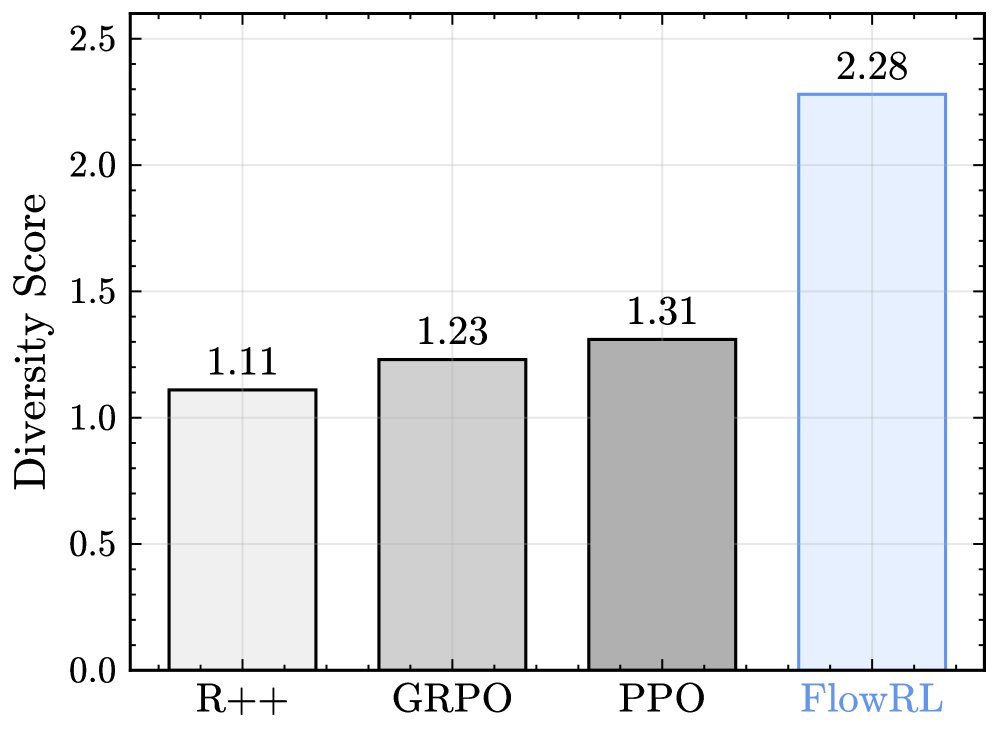
通过使用GPT-4评估不同方法在AIME数据集上生成的解法多样性，结果显示FlowRL的多样性得分显著高于所有基线。这经验性地证实了FlowRL的核心假设：流平衡优化能够促进模式覆盖，产生更多样化的解决方案，而不是对同一策略进行微小变动。

案例研究

下表展示了一个AIME问题的案例。GRPO反复尝试使用均值不等式（AM-GM），陷入了循环，最终未能解决问题。相反，FlowRL探索了不同的策略，通过假设 \(a=b\) 将问题转化为一个三次方程，并最终通过有理根定理找到了正确答案。这直观地展示了FlowRL如何通过多样性探索来避免陷入局部最优的推理模式。

总结

本文提出的FlowRL算法通过将RL的优化目标从奖励最大化转变为奖励分布匹配，并引入长度归一化和重要性采样解决了长序列推理中的实际挑战，最终在多个数学和代码推理任务上取得了SOTA性能。实验分析有力地证明，FlowRL通过提升探索多样性，有效避免了模式崩溃，从而增强了模型的泛化能力。