ForTIFAI: Fending Off Recursive Training Induced Failure for AI Models

TL;DR

本文提出了一种名为截断交叉熵（TCE）的置信度感知损失函数，通过在训练中忽略对高置信度预测的损失贡献，有效缓解了因循环使用合成数据进行训练而导致的模型崩溃现象。

关键定义

本文提出或沿用了以下对理解论文至关重要的核心概念：

相关工作

当前，生成式AI模型（如LLM）的持续发展依赖于海量且不断更新的训练数据。然而，随着模型生成的内容（即合成数据）在互联网上占比越来越高，用于训练下一代模型的数据集不可避免地会受到污染。

这种在合成数据上进行递归训练的现象会导致“模型崩溃”，即模型性能逐代下降。已有研究表明，即使是少量（如1%）的合成数据也可能引发崩溃，而简单地扩大模型或数据集规模并不能有效解决此问题。

先前的缓解策略包括将合成数据与真实数据混合、进行后处理监督或使用水印技术识别合成内容，但这些方法存在局限性，例如难以在实践中区分真实与合成数据。值得注意的是，作为模型学习核心的损失函数，其在缓解模型崩溃中的作用尚未得到充分关注。

本文旨在解决的核心问题是：如何通过改进训练过程来有效延缓或阻止因递归训练于合成数据而引发的模型崩溃。具体来说，本文将矛头指向了模型对其自身生成的合成数据存在的过度自信 (overconfidence) 问题。

本文方法

本文提出了一种名为 ForTIFAI 的模型无关框架，其核心思想是通过设计置信度感知的损失函数来缓解模型崩溃。

核心观察

本文的一个关键观察是，模型在处理其自身生成的合成数据时，会表现出比处理未见过的真实数据更高的预测置信度。

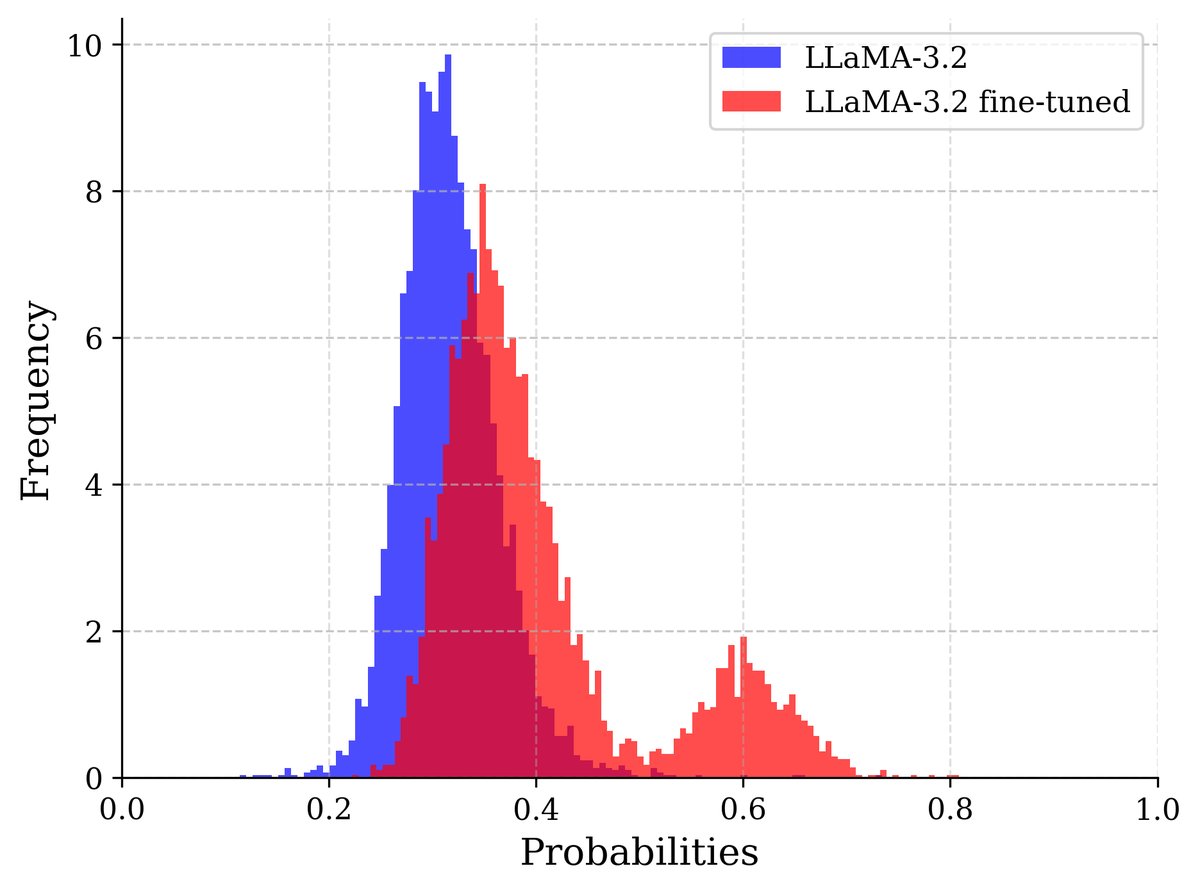模型在真实数据(a)和合成数据(b)上的置信度分布对比 (a) Wikitext上的置信度

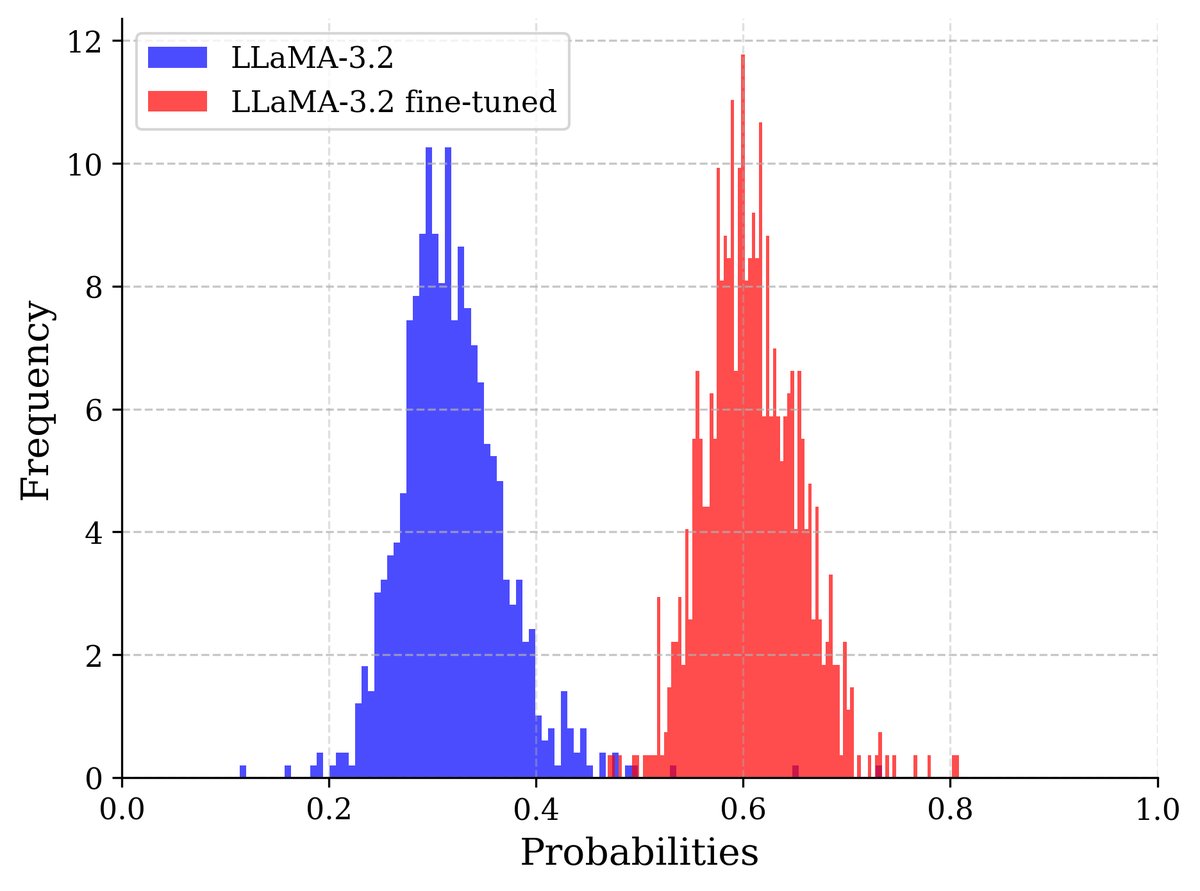模型在真实数据(a)和合成数据(b)上的置信度分布对比 (b) 再生Wikitext上的置信度

图1：模型在递归训练后对其自身生成的数据表现出更高的置信度。图中展示了LLaMA-3.2-1B模型及其在部分Wikitext上微调后的版本所分配的概率。微调后的模型在其训练过的Wikitext部分以及由它生成的整个数据集上都显示出更高的置信度，而原始模型在两种情况下的置信度分布相似。

如图1所示，这种置信度差距成为一个有用的信号，可以用来在训练中识别并降低合成数据的影响，从而减缓模型崩溃。

创新点：截断交叉熵 (TCE)

基于上述观察，本文提出了一种新颖的损失函数——截断交叉熵 (Truncated Cross Entropy, TCE)。与传统的交叉熵（CE）损失不同，TCE通过设置一个置信度阈值 $\gamma$，在计算损失时直接“截断”或屏蔽掉那些预测置信度超过该阈值的token。

其定义如下：

\[\text{TCE}(p_{t}) = \chi_{\gamma}(p_{t}) \times \text{CE}(p_{t})\] \[\chi_{\gamma}(p_{t}) = \begin{cases} 1 & \text{if } p_{t} \leq \gamma \\ 0 & \text{if } p_{t} > \gamma \end{cases}\]

通过这种方式，TCE迫使模型更多地从那些不确定、低置信度的样本中学习，而不是在已经“学会”的高置信度样本上过度拟合。这有助于保护数据分布的尾部，减缓因递归训练导致的分布坍缩。

优点

理论支撑

TCE对一维高斯估计器在全合成训练循环中的影响 图2：在一个全合成数据训练循环中，TCE对一维高斯分布估计器的影响。标准交叉熵（CE）导致方差迅速崩溃。相比之下，选择合适的阈值（γ=0.85）的TCE能显著延迟崩溃。

本文从一个简化的数学模型出发，为TCE的有效性提供了理论直觉。

  1. 在纯合成数据的自循环训练中，模型的估计方差会因采样偏差 $\lambda \le 1$ 而逐渐收缩，最终趋近于0，导致多样性丧失。

    \[\mathbb{E}[\sigma_{t} \mid \sigma_{t-1}] = \lambda \sigma_{t-1}, \quad \text{with } \lambda \leq 1, \qquad \Rightarrow \quad \sigma_{t} \xrightarrow{a.s.} 0.\]
  2. 为了对抗这种方差收缩，本文分析了一个一维高斯模型，并提出只对分布尾部（即低概率区域）的样本进行训练。

  3. 对截断后的分布进行训练，其条件方差会引入一个放大因子 $\eta(a) > 1$。

    \[\mathrm{Var}(X_{t} \mid \mid X_{t} \mid \geq a\sigma_{t}) = \eta(a) \cdot \sigma_{t}^{2}, \quad \text{where} \quad \eta(a) = 1 + \frac{a\,\phi(a)}{1-\Phi(a)} > 1\]

  4. 这样，方差的迭代关系变为：

    \[\mathbb{E}[\sigma_{t+1}^{2}] = \lambda \cdot \eta(a) \cdot \mathbb{E}[\sigma_{t}^{2}].\]
  5. 通过选择合适的截断阈值，可以使 $\lambda \cdot \eta(a) \approx 1$，从而稳定方差，延缓崩溃。

TCE正是这一思想的推广：通过忽略高置信度的预测，它将训练信号引向低置信度的、通常代表性不足的token，从而缓解分布尾部消失效应和统计误差的递归放大。

实验结论

实验框架

本文设计了一个模拟真实世界数据演变的实验框架。该框架从一个纯净的数据集开始，在每一代（stage）训练中，模型都会重新生成前一代的整个数据集，并与一部分新的真实数据混合，作为新一代模型的训练语料。随着迭代的进行，合成数据的比例越来越高。

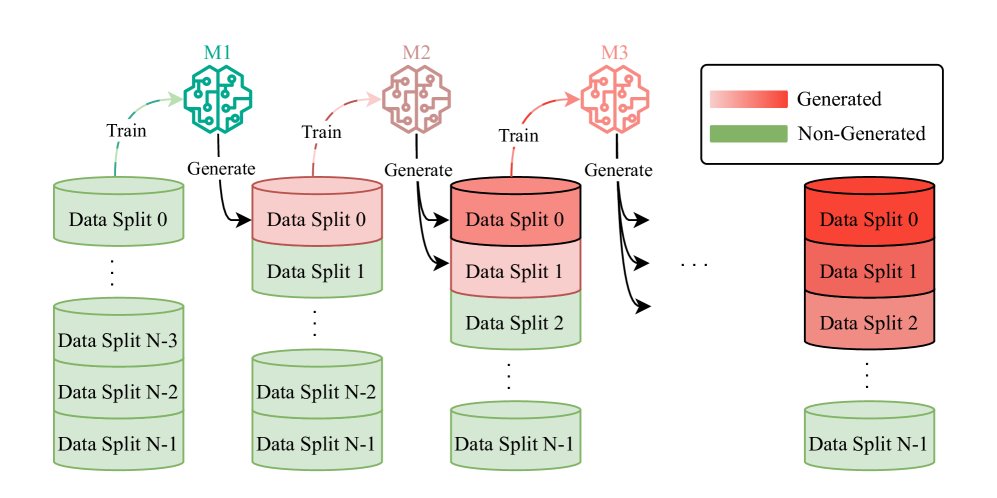实验设置模拟模型崩溃过程 图3：实验设置模拟模型崩溃，展示了从主要由人类生成的内容到大部分为合成数据集的过渡。$M_i$ 表示第 i 代递归训练的模型。在每一代，前一迭代的整个数据集被重新生成，并与一份新的干净数据合并，用于下一代模型的训练。

关键实验结果

1. LLM性能表现: 在Wikitext和更复杂的Imagination-of-Web（包含事实、常识和数学）数据集上，使用TCE训练的LLaMA和Gemma模型在多轮合成数据污染后，其性能（包括语法、常识、数学推理和知识保留）均显著优于使用标准交叉熵（CE）训练的基线模型。

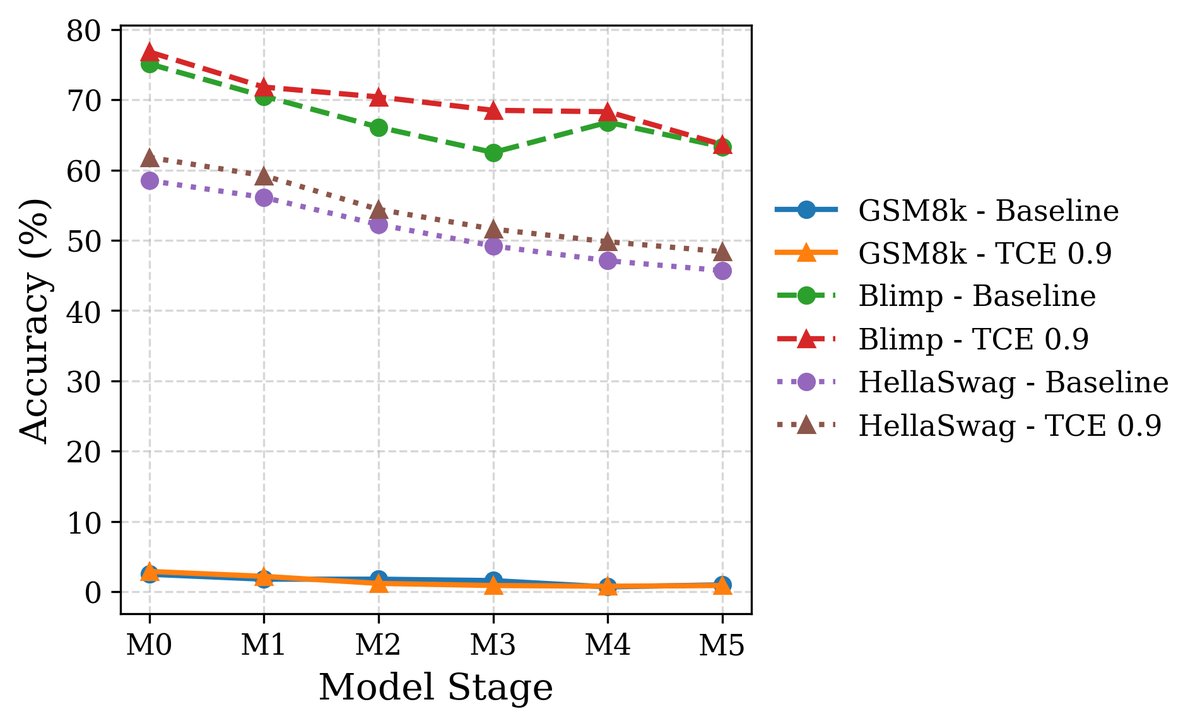TCE在不同数据集上的性能优于基线 (a) Wikitext

TCE在不同数据集上的性能优于基线 (b) Imagination

图5：在Wikitext和Imagination数据集上，TCE在所有基准测试中持续优于基线（CE）。

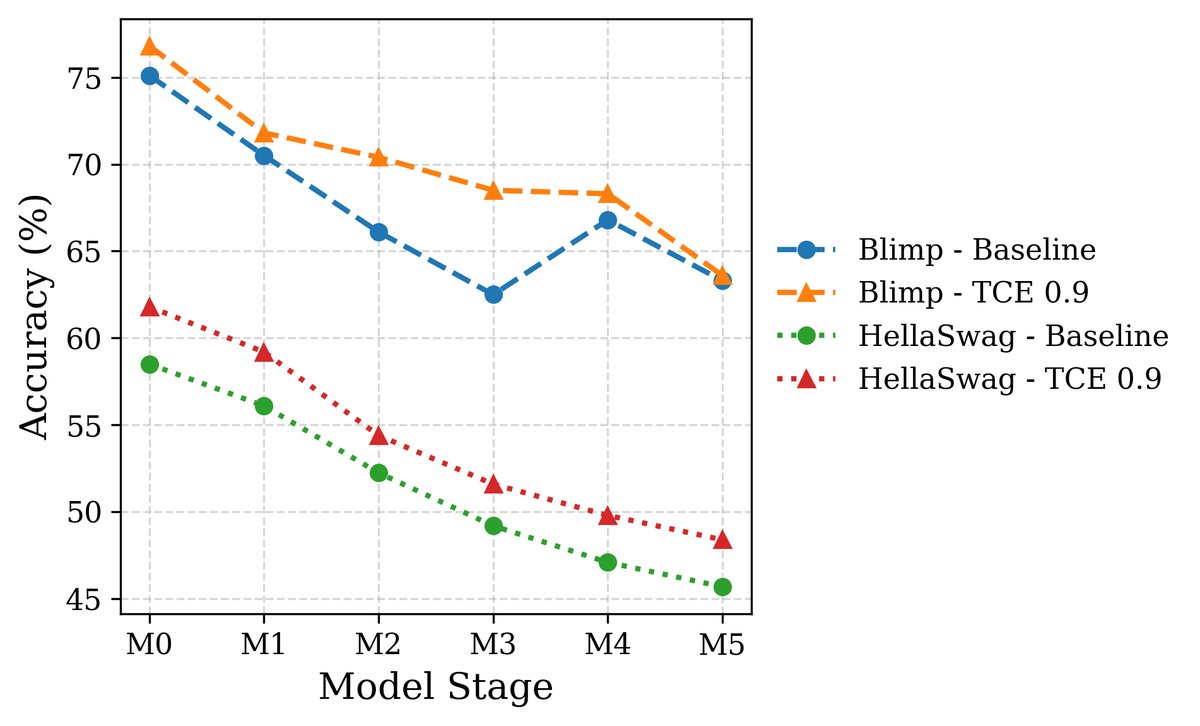
2. 失败时间延长: 在完全由合成数据迭代的子集上，TCE将模型的“失败时间”（KR-test准确率降至75%以下所需的迭代次数）从基线CE的不足两次迭代延长到了三次以上，时间延长超过2.3倍。

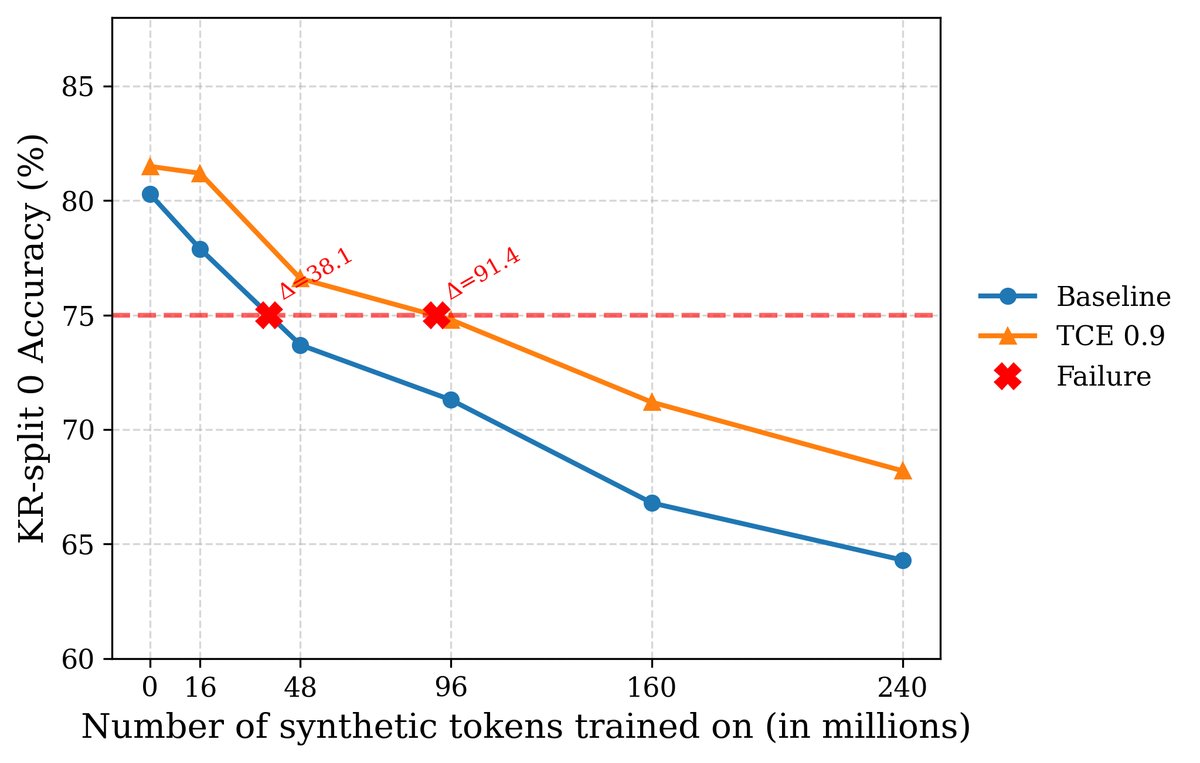TCE显著延长模型的失败时间 图6：在完全合成的数据子集上，TCE有效缓解模型崩溃。使用CE的模型在第二代就已崩溃，而TCE将崩溃点延迟到第三代之后。

3. 分布保真度: 通过测量生成数据分布与原始数据分布之间的KL散度，实验表明，使用TCE训练的模型其KL散度增长远慢于CE模型，说明TCE能更好地保持原始数据分布的多样性。

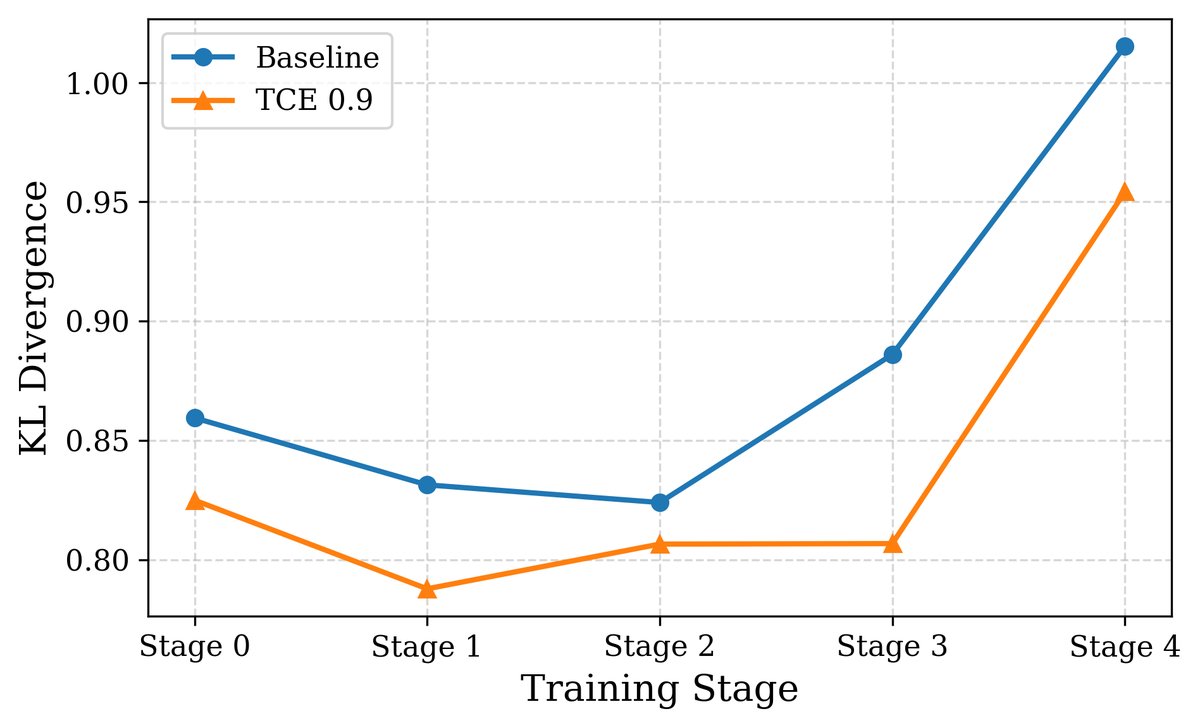TCE能更好地保持数据分布 (a) LLaMA-3.2-1B

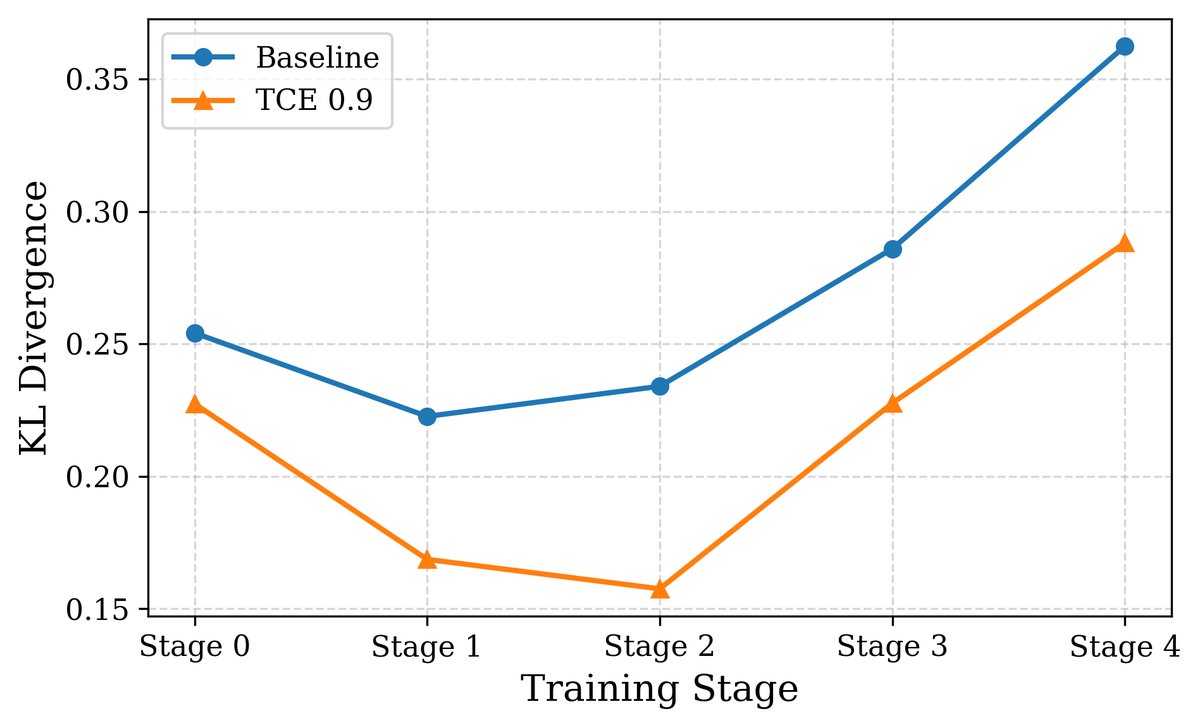TCE能更好地保持数据分布 (b) Gemma-3-1b-pt

图7：与CE相比，使用TCE训练的模型在多代递归训练后，其输出与原始数据分布的KL散度更低，表明其能更好地保持分布相似性。

4. 跨模态泛化: 本文将此方法成功应用于高斯混合模型（GMM）和变分自编码器（VAE）（用于图像生成）。结果表明，通过排除高可能性/高置信度的样本进行训练，同样可以有效延缓GMM的模式崩溃和VAE生成图像的质量退化，证明了该方法的普适性。

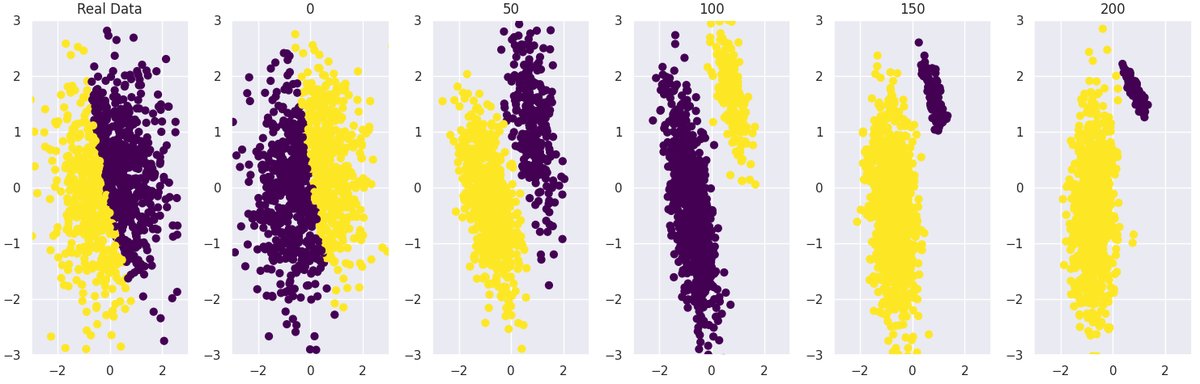GMM中的模型崩溃与缓解 基线GMM快速崩溃 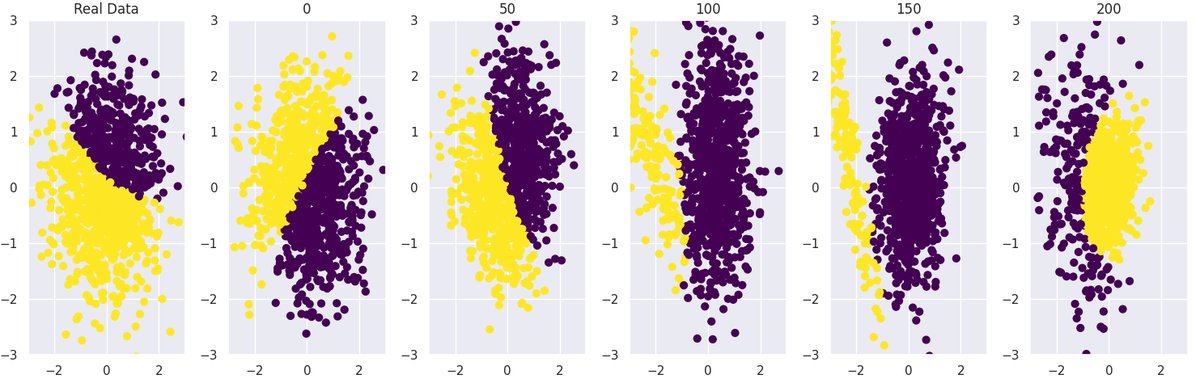GMM中的模型崩溃与缓解 截断训练的GMM有效延迟崩溃 图8：在高斯混合模型（GMM）中，标准训练（上图）导致模式迅速崩溃，而本文提出的截断方法（下图）显著延迟了崩溃，更久地保留了数据结构。

VAE中的模型崩溃与缓解 图9：在VAE图像生成中，使用CE训练（上行）导致所有数字的生成形状趋同（崩溃），而使用本文方法（下行）则在多轮迭代中保持了每个数字的独特结构。

总结

实验结果有力地证明，截断交叉熵（TCE）是一种简单、高效且模型无关的策略，能通过解决模型对自生成数据的过度自信问题，显著缓解模型崩溃。它不仅在各种任务和模型上优于标准交叉熵，还能将模型的有效寿命延长超过2.3倍，同时其核心思想能够成功泛化到文本之外的其他生成领域。

未来方向