GaLLoP: Gradient-based Sparse Learning on Low-Magnitude Parameters
-
ArXiv URL: http://arxiv.org/abs/2510.19778v1
-
作者: Antoine Bosselut; Lukas Mauch; Fabien Cardinaux
-
发布机构: EPFL; Sony Europe Ltd.; University of Stuttgart
TL;DR
本文提出了一种名为 GaLLoP 的稀疏微调新方法,它通过优先选择在下游任务上梯度最大、且在预训练模型中权重绝对值最小的参数进行微调,从而在提升任务性能的同时有效保留预训练知识,实现了卓越的分布内(ID)和分布外(OOD)泛化能力。
关键定义
本文提出或重点使用了以下核心概念:
-
GaLLoP (Gradient-based Sparse Learning on Low-Magnitude Parameters):本文提出的核心方法。一种稀疏微调技术,其参数选择标准是:同时满足在下游任务上具有高梯度幅度和在预训练模型中具有低权重幅度。这一双重标准旨在平衡任务适应性和知识保留。
-
稀疏微调 (Sparse Fine-Tuning, SpFT):一种参数高效微调(PEFT)策略,它仅更新模型原始参数的一小部分稀疏子集,而保持其余参数冻结,从而在不引入额外参数的情况下适配下游任务。
-
遗忘率 (Forget Ratio):本文提出的一个新评估指标,用于量化微调过程中发生的灾难性遗忘。它衡量了模型在分布外(OOD)任务上的性能相对于零样本(vanilla)模型的性能下降比例。其定义如下:
\[\text{Forget Ratio}_{r}=\max\left(0,\dfrac{\text{Accuracy}_{\text{Vanilla},\,r}^{\text{OOD}}-\text{Accuracy}_{r}^{\text{OOD}}}{\text{Accuracy}_{\text{Vanilla},\,r}^{\text{OOD}}}\right)\]理想情况下,该比率应为0,表示没有知识遗忘。
-
崩溃率 (Collapse Rate):本文提出的另一个新评估指标,用于量化微调导致的灾难性记忆。它计算的是模型在所有分布外(OOD)任务中,有多少个任务的准确率降至约等于0%(即性能完全崩溃)的比例。其定义如下:
\[\text{Collapse Rate}_{r}=\sum_{\begin{subarray}{c}n=1\\ n\neq{f_{r}}\end{subarray}}^{N^{D}}\mathbf{1}[\lfloor\text{accuracy}({\mathcal{D}_{test}^{n}})\rfloor=0\]\]理想情况下,该比率应为0,表示没有发生灾难性记忆。
相关工作
当前的大语言模型(LLM)微调领域,参数高效微调(PEFT)技术是主流。这些技术主要分为三类:
- 附加模块法:如Adapter,通过在模型中添加新模块进行训练。缺点是会引入额外的推理延迟。
- 低秩重参数化法 (Reparametrization-based Fine-Tuning, RFT):如LoRA、DoRA,通过低秩分解来近似权重更新。这类方法虽然高效,但仍然容易过拟合,导致灾难性遗忘和对训练数据的过度记忆。
- 稀疏微调法 (Sparse Fine-Tuning, SpFT):直接微调模型固有参数的一小部分。这类方法的关键瓶颈在于如何选择最合适的参数子集进行更新。现有方法通常采用单一标准,例如:
- 选择梯度最大的参数(如SAFT, SIFT),侧重于任务相关性。
- 选择预训练权重最小的参数(如PaFi),侧重于保留重要知识。
本文旨在解决的核心问题是:如何设计一种更优的参数选择策略,以同时提升模型的分布内(In-Distribution, ID)泛化能力(即任务性能)和分布外(Out-of-Distribution, OOD)泛化能力(即知识保留),从而克服现有方法的局限性。
本文方法
动机
为了平衡ID和OOD泛化,微调算法必须既能最小化下游任务的损失,又能最大限度地保留预训练知识。高梯度参数对于任务收敛至关重要,但直接微调它们可能损害预训练模型中已有的重要知识。
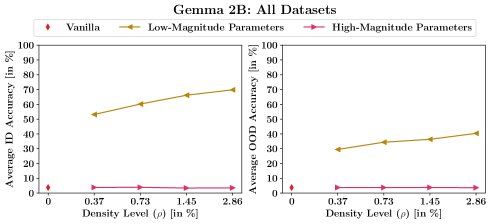
本文通过一个初步实验来验证假设:微调低幅度的预训练参数对保留知识更有利。实验结果表明,仅微调预训练权重幅度最小的参数,能够显著提升ID和OOD性能;而微调幅度最大的参数则几乎没有效果,性能与未微调的原始模型相当。这一发现支持了本文的核心假设:微调低幅度参数有助于增强预训练知识的利用。
GaLLoP 算法
基于上述动机,本文提出了GaLLoP算法。其核心思想是,在给定的稀疏度 $\rho$ 下,选择并微调那些同时满足“高梯度”和“低幅度”的参数。该算法分为两个阶段:
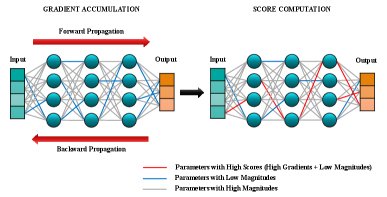
阶段一:参数选择
-
计算梯度:首先,在下游任务数据集 $\mathcal{D}$ 的一个小子集上计算模型参数 $\mathbf{\theta}$ 相对于损失函数 $\mathcal{L}$ 的梯度向量 $\mathbf{g}$。
\[\mathbf{g}=\dfrac{1}{d_s N}\sum_{n=1}^{d_s N}\nabla_{\mathbf{\theta}}\mathcal{L}(\mathbf{x}_n,\mathbf{y}_n;\mathbf{\theta})\]这满足了“高梯度”这一选择标准。
-
计算分数:为了同时满足“低幅度”标准,本文设计了一个分数向量 $\mathbf{s}$,其计算方式如下:
\[\mathbf{s}=\left(\dfrac{\text{abs}(\mathbf{g})}{\text{abs}(\mathbf{\theta})+\epsilon}\right)\]其中,$\text{abs}(.)$ 计算逐元素的绝对值,$\epsilon$ 是一个很小的数(如 $10^{-8}$)以防止分母为零。这个分数直接体现了“高梯度/低幅度”的比率。
-
生成掩码:根据分数向量 $\mathbf{s}$,选出分数最高的 $\rho\%$ 的参数。具体方法是计算一个分数阈值 $s_t$,然后生成一个二元掩码向量 $\mathbf{m}$。对于每个参数,如果其分数大于等于阈值,则掩码值为1(表示被选中进行微调),否则为0。
\[\mathbf{m}_i=\begin{cases}1&\text{if }\mathbf{s}_i\geq s_t,\\ 0&\text{otherwise.}\end{cases}\]
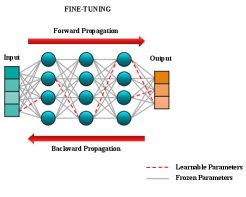
阶段二:稀疏微调
在获得掩码 $\mathbf{m}$ 后,使用标准的梯度下降法(如mini-batch GD)进行模型微调。在反向传播更新参数时,只更新掩码值为1的参数,而其他参数保持冻结。
创新点
GaLLoP的核心创新在于其双重标准参数选择得分函数。与之前仅依赖梯度(如SAFT)或仅依赖权重幅度(如PaFi)的稀疏微调方法不同,GaLLoP首次将两者结合,形成一个统一的、更有原则性的选择标准。这种设计使得算法能够:
- 通过高梯度标准,确保所选参数与下游任务高度相关,从而提升ID性能。
- 通过低幅度标准,避免修改预训练模型中被认为更重要的高幅度参数,从而有效保留预训练知识,提升OOD性能,并减少灾难性遗忘。
实验结论
本文在LLaMA3 8B和Gemma 2B模型上,针对8个常识推理数据集进行了详尽的实验,并将GaLLoP与全量微调(FFT)、LoRA、DoRA、SAFT、SpIEL等多种SOTA方法进行了比较。
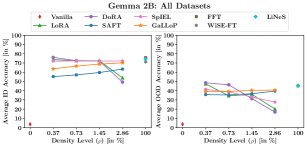
ID 和 OOD 准确率
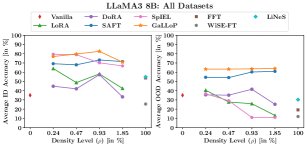
- 性能卓越:GaLLoP在ID和OOD准确率上均表现出色。对于LLaMA3 8B,GaLLoP在所有稀疏度下都构成了ID与OOD性能的帕累托最优前沿,显著优于其他所有对比方法。
- 优于SAFT:GaLLoP稳定地超越了同样基于梯度的SAFT方法,ID和OOD平均准确率高出约10%,证明了其双重选择标准的优越性。
- 对“过度预训练”鲁棒:在LLaMA3 8B这类经过海量数据预训练的模型上,FFT等方法性能严重下降,而GaLLoP依然表现稳健,展示了其对不同预训练程度模型的鲁棒性。
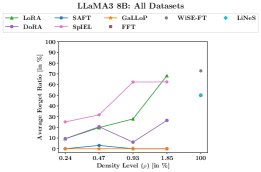
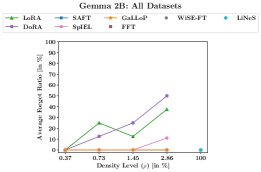
灾难性遗忘
- 零遗忘:通过本文提出的遗忘率指标进行衡量,GaLLoP在所有实验设置和稀疏度下均实现了 0% 的遗忘率。
- 对比方法表现不佳:相比之下,LoRA、DoRA、FFT等方法均表现出明显的灾难性遗忘,尤其是在LLaMA3 8B上,其遗忘率随可训练参数密度的增加而升高。
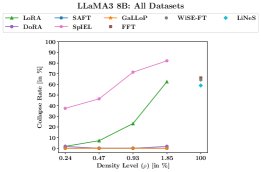
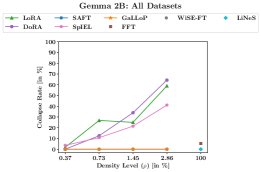
灾难性记忆
- 零崩溃:通过崩溃率指标进行衡量,GaLLoP和SAFT都实现了 0% 的崩溃率,即在任何OOD任务上性能都不会完全崩溃。
- 其他方法的记忆问题:相比之下,RFT(LoRA, DoRA)和SpIEL等方法在部分OOD任务上会因过度拟合ID任务的数据模式(如回答格式、高频词汇)而导致性能崩溃。在更极端的情况下,FFT和SpIEL甚至会导致模型只生成EOS token。
稳定性
实验还表明,GaLLoP在不同随机种子下的性能表现更加稳定,方差更小,说明其训练过程更为可靠。
总结
实验结果全面证实了GaLLoP方法的有效性。通过其创新的双重标准参数选择策略,GaLLoP在不牺牲OOD泛化能力的前提下,显著提升了ID任务性能。它成功地缓解了灾难性遗忘和记忆问题,在性能、鲁棒性和稳定性方面均优于现有的多种主流PEFT技术。