Graph of Thoughts: Solving Elaborate Problems with Large Language Models

• ArXiv URL: http://arxiv.org/abs/2308.09687v4

• 作者: Maciej Besta; Michal Podstawski; H. Niewiadomski; Aleš Kubíček; Torsten Hoefler; Robert Gerstenberger; P. Nyczyk; Lukas Gianinazzi; Joanna Gajda; Tomasz Lehmann; 等1人

• 发布机构: Cledar; ETH Zurich; Warsaw University of Technology

---

TL;DR

本文提出了一种名为“思想图谱 (Graph of Thoughts, GoT)”的新型提示框架，通过将大型语言模型 (LLM) 的思维过程建模为任意图结构，其中“思想”是节点，依赖关系是边，从而实现了超越链式或树状思维模式的、更复杂和强大的推理能力，尤其擅长聚合多个推理路径以生成协同的、更高质量的解决方案。

关键定义

• 思想图谱 (Graph of Thoughts, GoT)：一个将 LLM 推理过程建模为图 \(G = (V, E)\) 的框架。其中，每个节点 \(v ∈ V\) 代表一个“思想”（即 LLM 生成的一个完整的解决方案或部分解决方案），每条有向边 \((u, v) ∈ E\) 代表思想 \(v\) 是基于思想 \(u\) 生成的。这种图结构允许思想之间存在任意复杂的依赖关系，是本文最核心的贡献。
• 思想变换 (Thought Transformations)：指在 GoT 框架中对思想图谱进行修改以推进推理过程的操作。本文定义了三大类图驱动的变换：
  1. 聚合 (Aggregation)：将多个并行的思想节点合并成一个新节点，以综合不同推理路径的优点。这是 GoT 区别于以往方法的关键能力。
  2. 提炼 (Refining)：对单个思想节点进行迭代式优化，通过创建一个指向自身的环 \((v, v)\) 来表示。
  3. 生成 (Generation)：从一个现有思想节点派生出多个新的思想节点，类似于树状搜索中的分支。
• 思想的操作图 (Graph of Operations, GoO)：一个静态的数据结构，由用户预先定义，用于规划整个任务的执行流程。它规定了在推理过程中需要执行哪些思想变换（如生成、聚合、评分），以及这些操作的顺序和依赖关系。
• 思想的体积 (Volume of a thought)：本文提出的一个新指标，用于衡量某个思想 \(t\) 背后潜在的信息量。其定义为在思想图谱中，能够通过有向路径到达思想 \(t\) 的所有前驱思想的总数。体积越大，代表该思想综合了越多的先前信息。

相关工作

当前，提升大型语言模型 (LLM) 推理能力的主流提示工程 (Prompt engineering) 方法包括：

1. 思维链 (Chain-of-Thought, CoT)：通过引导 LLM 生成一系列中间推理步骤来解决复杂问题，但其线性结构限制了探索的广度。
2. 自洽性思维链 (Self-Consistency with CoT, CoT-SC)：通过生成多条独立的思维链并投票选出最佳答案，增加了鲁棒性，但各分支间无法交互。
3. 思维树 (Tree of Thoughts, ToT)：将推理过程建模为一棵树，允许在不同分支上进行探索、评估和回溯，比 CoT 更灵活。

然而，这些方法存在一个共同的瓶颈：它们的结构（链式或树状）过于刚性。它们无法自然地表达一种在复杂问题解决中至关重要的能力：合并或融合多个不同的推理路径。例如，人类在解决问题时，可能会探索一条思路，然后转而探索另一条，最后发现可以将两条思路中的优点结合起来，形成一个更优的解决方案。现有的提示方法无法实现这种“思想的聚合”。

本文旨在解决这一问题，通过引入图结构，提供一个更通用、更强大的推理范式，以释放 LLM 更复杂的推理潜力。

本文方法

本文的核心是提出了 Graph of Thoughts (GoT) 框架，它将 LLM 的推理过程从线性链条或树状结构推广到了通用的图结构，从而实现了更高级的思维操作。

GoT 核心思想

GoT 将整个推理过程形式化为一个元组 \((G, T, E, R)\)，包含四个核心要素：

• 推理过程图 (G)：一个有向图 \(G = (V, E)\)，节点 \(V\) 是 LLM 的思想，边 \(E\) 是思想间的依赖。这种结构允许一个思想节点拥有多个父节点，这是实现“聚合”的关键。
• 思想变换 (T)：对图 \(G\) 进行操作的函数，用以推进推理。
• 评估器 (E)：一个评分函数，用于评估每个思想的质量。
• 排序器 (R)：一个排序函数，用于筛选出最重要的思想。

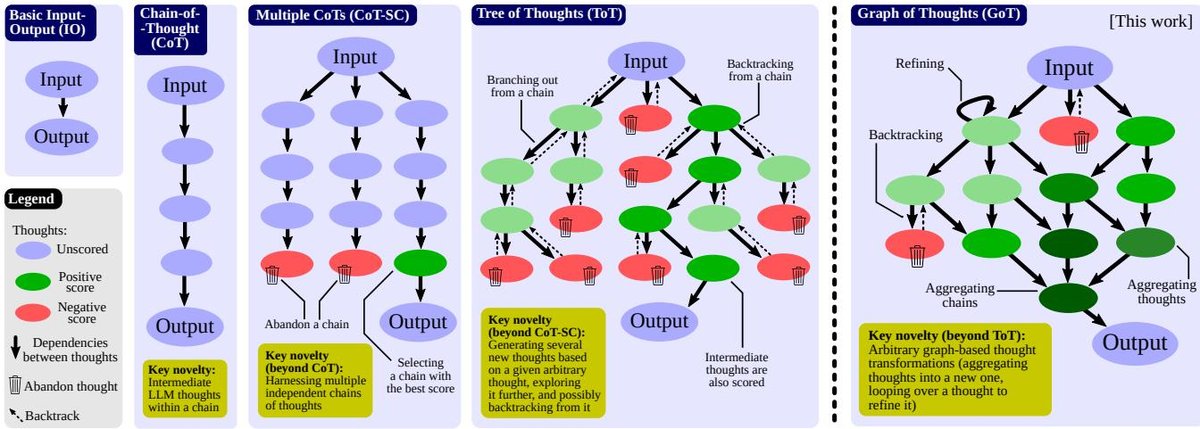图1：GoT 与其他提示策略（IO, CoT, ToT）的比较。GoT 的图结构可以无缝地概括 CoT 和 ToT，并增加了聚合等新能力。

创新点：图驱动的思想变换

GoT 的图模型催生了新的思想变换能力，超越了以往的方法。

• 聚合 (Aggregation)：允许将多个思想 \(v1, ..., vk\) 的信息融合成一个新的思想 \(v+\)。这在图上表现为创建一个新节点 \(v+\)，并从 \(v1, ..., vk\) 向其引出多条边。这一变换使得 GoT 非常适合于“分而治之”策略，即将一个大问题分解成多个子问题，独立解决后再将子答案合并。
• 提炼 (Refining)：通过迭代循环来优化单个思想，图上表现为一个自环 \((v, v)\)。
• 生成 (Generation)：从一个思想 \(v\) 派生出多个新思想 \(v+1, ..., v+k\)，类似于 ToT 的分支操作。

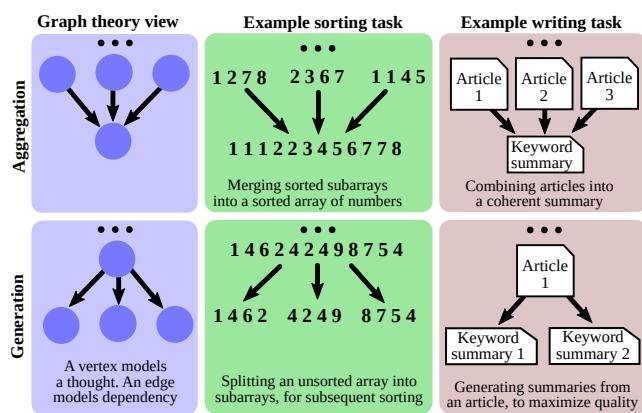图2：聚合（左）和生成（右）思想变换的示例。聚合将多个输入思想合并成一个，而生成则从一个思想派生出多个。

GoT 系统架构

为了将 GoT 思想付诸实践，本文设计了一个模块化的系统架构，确保了灵活性和可扩展性。 图3：GoT 的系统架构概览（蓝色部分）、模块 API（绿色部分）及示例（红色部分）。

该架构主要包括：

• 控制器 (Controller)：整个系统的“大脑”，负责协调所有模块。它根据思想的操作图 (Graph of Operations, GoO) 来制定执行计划，并维护着图推理状态 (Graph Reasoning State, GRS)，一个记录当前所有思想及其状态的动态结构。GoO 是用户预定义的静态任务分解图，而 GRS 是执行中的动态产物。
• 提示器 (Prompter)：根据控制器指令，负责生成发送给 LLM 的具体提示 (prompt)。
• 解析器 (Parser)：负责从 LLM 的回复中提取结构化信息，并更新 GRS。
• 评分与验证模块 (Scoring & Validation)：负责验证 LLM 输出的正确性并为其打分，评分结果会反馈给控制器用于决策。

这个架构不仅实现了 GoT，也能够通过配置 GoO 来模拟 CoT、ToT 等现有方案，并支持方便地扩展新的思想变换和集成不同的 LLM 模型。

案例应用：排序任务

以排序任务为例，GoT 的应用流程如下：

1. 定义 GoO：将排序任务分解为“分、治、合”三个阶段。
   • 分解：将一个长数字序列（如64个数字）分解成多个独立的子序列（如8个长度为8的子序列）。
   • 排序：并行地让 LLM 对每个子序列进行排序（这是一个LLM更容易解决的小任务）。
   • 合并：分层地、两两合并已排序的子序列，直到最终得到一个完全排序的序列。
2. 执行：控制器根据 GoO 的规划，调用 LLM 完成每一步，并用评分函数评估中间结果的质量。

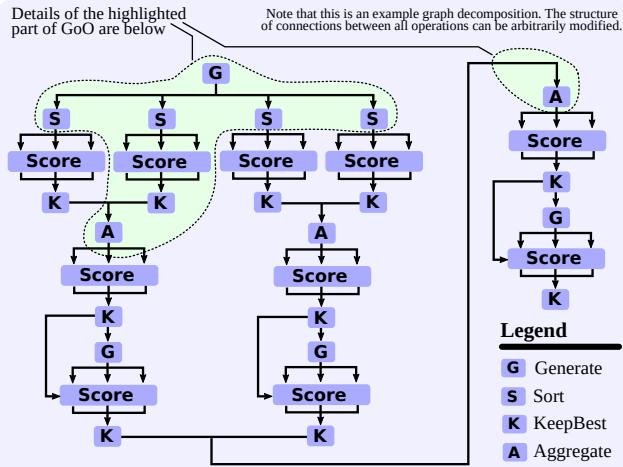图4：一个将64个数字排序任务分解为子任务的GoO示例。

通过这种方式，GoT 将一个 LLM 难以一次性完美解决的复杂任务，转化成了一系列 LLM 可以高质量完成的简单子任务，最后通过聚合操作得到高质量的最终解。

实验结论

本文通过在排序、集合交集、关键词计数和文档合并等多个任务上的实验，验证了 GoT 框架的有效性。

实验结果

• 性能优势：在所有测试任务上，GoT 的表现均显著优于 IO、CoT 和 ToT 等基线方法。例如，在排序128个数字的任务中，GoT 的中位误差比 ToT 低约 62%，同时成本还降低了 31% 以上。
• 处理复杂问题的能力：GoT 的优势随着问题复杂度的增加而愈发明显。对于更长序列的排序或更大规模的集合运算，GoT 的性能领先幅度更大，而 IO 和 CoT 等简单方法的性能则急剧下降。这证明了 GoT 的思想分解与聚合机制对于解决复杂问题至关重要。

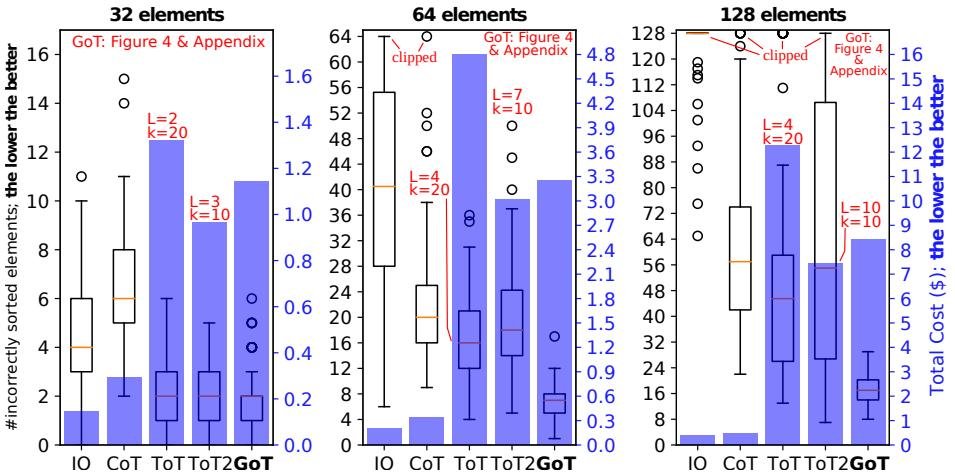图5：排序任务中的错误数量与成本。GoT 在保证更低错误率的同时，成本也低于性能最好的 ToT 配置。

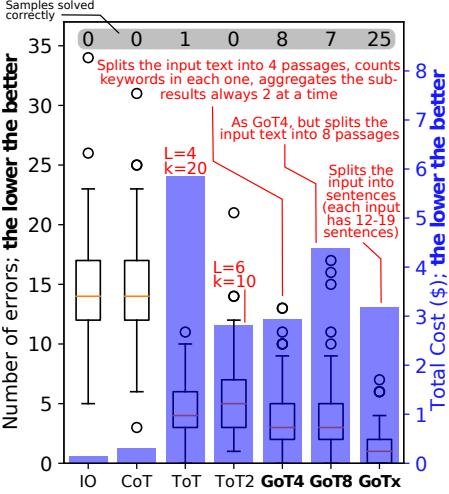图6：集合交集任务中的错误数量与成本。GoT 同样展现出最佳的性能与成本效益。

• 成本与分解粒度的权衡：实验表明，任务分解的粒度是一个关键因素。将任务分解到 LLM 可以轻松解决的子任务级别，可以显著减少后续所需的修正和改进步骤，从而在整体上获得更高效率。

理论分析：延迟-体积权衡

本文还从理论上分析了不同提示策略的延迟（Latency）与思想体积（Volume）之间的权衡。延迟指获得最终答案所需的最少推理步数，体积指最终答案能融合多少先前信息。

方案	延迟	体积
Chain-of-Thought (CoT)	\(N\)	\(N\)
Self-Consistency with CoT (CoT-SC)	\(N/k\)	\(N/k\)
Tree of Thoughts (ToT)	\(log_k(N)\)	\(O(log_k(N))\)
Graph of Thoughts (GoT)	\(log_k(N)\)	\(N\)

表格2：不同提示方案在延迟与体积权衡上的比较。

分析表明，GoT 是唯一能够同时实现低延迟（\(log_k(N)\)）和高体积（\(N\)）的方案。这得益于其独特的聚合能力，使得最终思想可以汇集来自整个推理图谱的信息，而不仅仅是一条路径或一棵子树。

最终结论

GoT 框架通过将 LLM 的推理过程建模为图，实现了对思想的聚合、提炼和生成等高级操作。它特别适用于那些可以被分解为子任务然后合并结果的复杂问题。实验和理论分析均表明，GoT 在提升解决方案质量和处理复杂问题方面，相比 CoT 和 ToT 等现有最先进方法具有显著优势，同时还能有效控制推理成本，代表了提示工程领域一个重要且更强大的范式。