Harnessing Uncertainty: Entropy-Modulated Policy Gradients for Long-Horizon LLM Agents
-
ArXiv URL: http://arxiv.org/abs/2509.09265v1
-
作者: Jiacai Liu; Yuqian Fu; Yingru Li; Ke Wang; Yu Yue; Xintao Wang; Yuan Lin; Yang Wang; Jiawei Wang; Lin Zhang
-
发布机构: ByteDance
TL;DR
本文提出了一种名为熵调制策略梯度 (Entropy-Modulated Policy Gradients, EMPG) 的框架,通过利用智能体在长时程任务中每一步的内在不确定性(熵)来动态调整策略梯度,从而有效解决了稀疏奖励下的信用分配难题,显著提升了大型语言模型(LLM)智能体的学习效率和最终性能。
关键定义
本文的核心是围绕利用模型内在不确定性来重塑强化学习信号。关键定义如下:
- 熵调制策略梯度 (Entropy-Modulated Policy Gradients, EMPG):本文提出的核心框架。它不依赖外部的密集奖励信号,而是通过智能体在决策过程中产生的内在不确定性(以策略熵量化)来调制(re-calibrate)策略梯度。该框架包含“自校准梯度缩放”和“未来清晰度奖励”两个关键组件。
- 步级不确定性 (Step-Level Uncertainty):对智能体在每个“思考-行动”循环中的置信度的量化。本文采用一个实用且高效的代理指标:在一个步骤中生成的所有token的平均熵。低熵代表高置信度,高熵代表不确定。
- 自校准梯度缩放 (Self-Calibrating Gradient Scaling):EMPG的第一个核心组件。它是一个缩放函数,根据当前步骤的熵来调整从最终任务结果分配到的学习信号。其关键作用是:放大高置信度(低熵)步骤的梯度,同时衰减低置信度(高熵)步骤的梯度。
- 未来清晰度奖励 (Future Clarity Bonus):EMPG的第二个核心组件。这是一种内在奖励(intrinsic motivation),用于鼓励智能体选择那些能够导向更确定、更清晰未来状态(即下一步骤熵更低)的行动。
相关工作
目前,基于大型语言模型(LLM)的自主智能体在处理长时程任务时面临一个核心瓶颈:由于奖励信号极其稀疏(通常仅在任务结束时才提供),导致难以准确地为中间的关键步骤进行信用分配。
为了解决这一问题,当前的研究主要分为两个方向:
- 隐式奖励引导:通过传统的强化学习技术(如奖励塑造、内在好奇心、逆向强化学习)来创造密集的奖励信号。然而,这些方法在面对LLM智能体任务固有的巨大状态和动作空间时,往往计算成本过高、难以扩展或严重依赖人类先验知识。
- 显式步级监督:采用过程奖励模型 (Process Reward Models, PRMs) 为每一步提供反馈。但PRMs的构建需要高昂的人工标注成本,且在复杂交互任务中定义“正确”的单一步骤本身就是一个难题,导致其泛化能力差、不切实际。
此外,一些工作尝试将策略熵用作学习信号,但要么因“自信地犯错”而存在风险,要么应用范围局限于单轮生成任务,未能解决多步决策中的信用分配问题。
本文旨在解决上述方法未能有效处理的长时程、多步决策任务中的信用分配难题。具体而言,本文首先从理论上揭示了策略梯度大小与策略熵天然耦合的问题——高熵(不确定)行为产生大梯度,低熵(自信)行为产生小梯度,这导致学习效率低下且不稳定。本文的目标就是直接修正这一内在的梯度动态。
本文方法
本文提出了熵调制策略梯度(EMPG)框架,旨在通过重新校准策略梯度的学习动态来解决长时程智能体任务中的信用分配问题。其核心思想是利用智能体内在的、逐级的不确定性来调制学习信号。
理论动机
本文首先从理论上分析了策略梯度与策略不确定性之间的关系。如 命题1 (Proposition 1) 所示,对于标准的softmax策略,分数函数(score function)的期望L2范数的平方与策略的Rényi-2熵呈单调关系:
\[\mathbb{E}_{a\sim\pi_{\theta}(\cdot \mid s)}\left[ \mid \mid \nabla_{z_{\theta}(s)}\log\pi_{\theta}(a \mid s) \mid \mid ^{2}\right]=1-\exp(-H_{2}(\pi))\]这揭示了一个固有的学习动态:高熵(不确定)的步骤会自然产生大幅度的梯度,可能导致训练不稳定;而低熵(自信)的步骤则产生小幅度的梯度,即使这些步骤是正确的,其强化效果也有限,从而降低了学习效率。EMPG正是为了直接解决这个双重挑战而设计的。
创新点
EMPG的创新在于引入了一个新的调制后优势函数 (Modulated Advantage) $A_{\text{mod}}$,它取代了传统强化学习中对一整个轨迹使用统一优势值的做法,为每个决策步骤 $t$ 定制了学习信号:
\[A_{\text{mod}}(i,t)=\underbrace{A^{(i)}\cdot g(H_{t}^{(i)})}_{\text{自校准梯度缩放}}+\underbrace{\zeta\cdot f(H_{t+1}^{(i)})}_{\text{未来清晰度奖励}}\]其中,$A^{(i)}$ 是轨迹 $i$ 的最终回报优势,$H_{t}^{(i)}$ 是第 $t$ 步的熵。该优势函数由两个核心组件构成:
1. 自校准梯度缩放 $g(H)$
这个组件旨在修正上述理论动机中发现的梯度-熵耦合问题。
- 功能:根据当前步骤的熵 $H_t$ 来放大或缩小基础优势信号 $A^{(i)}$。
- 设计:它通过一个以batch为单位进行归一化的指数函数实现,确保其在mini-batch上的均值为1,只重新分配信号,而不改变其总量,从而保证训练的稳定性。
- 优点:
- 对于自信且正确的步骤(低熵,$A^{(i)}>0$),$g(H) > 1$,梯度被放大,从而加速学习。
- 对于自信但错误的步骤(低熵,$A^{(i)}<0$),$g(H) > 1$,惩罚被加强,有效抑制“幻觉式自信”。
- 对于不确定的步骤(高熵),$g(H) < 1$,梯度被衰减,防止了探索性行动带来的噪声对策略更新造成干扰,增强了训练稳定性。
2. 未来清晰度奖励 $f(H)$
这个组件为智能体提供了一种内在激励,以引导其进行更有目的性的探索。
- 功能:提供一个额外的奖励信号,其大小与下一步骤的置信度(低熵)成正比。
- 设计:它是一个简单的指数函数,鼓励智能体选择那些能导向更少模糊性、更可预测的未来状态的行动。
- 优点:通过鼓励智能体主动寻求清晰的解题路径,引导其远离混乱和高熵的轨迹,从而学会一种通用的元技能:在模糊环境中主动寻求确定性。
算法流程
EMPG的整体算法流程如下:
- 收集数据:运行当前策略 $\pi_{\theta}$,收集一批轨迹。
- 计算基础优势:对每条轨迹根据其最终任务结果(成功/失败)计算一个轨迹级别的优势值 $A^{(i)}$。
- 计算步级熵:计算该批次中所有轨迹、所有步骤的熵 $H_t$。
- 归一化与计算调制因子:在批次内对熵进行归一化,然后计算自校准缩放因子 $g(H_t)$ 和未来清晰度奖励 $f(H_{t+1})$。
- 计算调制后优势:使用公式计算每个步骤的 $A_{\text{mod}}(i,t)$。
- 最终归一化:对所有 $A_{\text{mod}}$ 进行批次归一化(零均值),得到最终的优势信号 $A_{\text{final}}(i,t)$。
- 更新策略:使用 $A_{\text{final}}$ 作为优势函数,通过策略梯度方法更新模型参数 $\theta$。
实验结论
本文在WebShop、ALFWorld和Deep Search三个具有挑战性的长时程智能体基准任务上进行了广泛实验,结果表明EMPG取得了显著且一致的性能提升。
主要结果
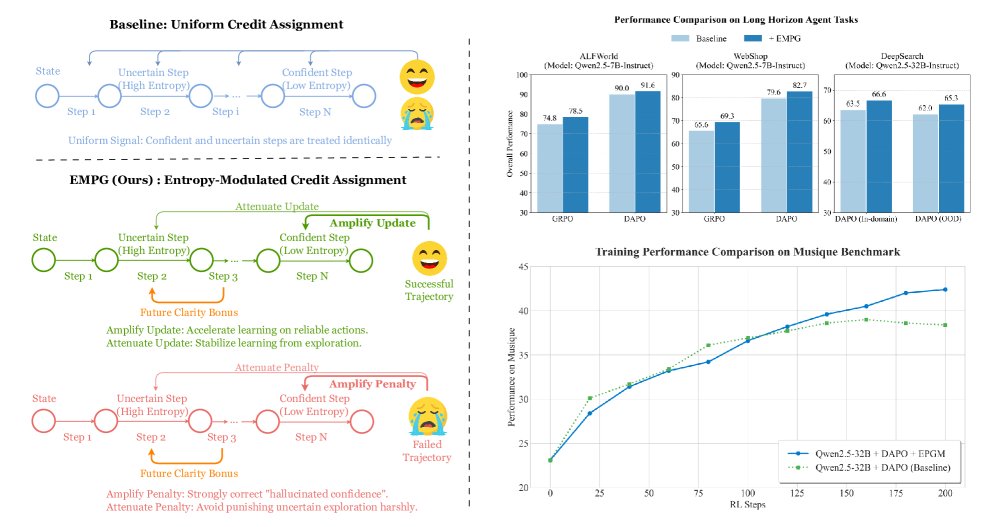
- 对现有RL算法的显著增强:在ALFWorld和WebShop任务上(见表1),EMPG作为一种即插即用的模块,能够稳定提升GRPO和DAPO等强基线方法的性能。例如,在Qwen2.5-7B模型上,EMPG将DAPO在WebShop上的成功率从79.6%提升至82.7%。
| 方法 | ALFWorld (All) | WebShop (Succ.) |
|---|---|---|
| 基线: Qwen2.5-1.5B-Instruct | ||
| GRPO* | 65.6 | 58.2 |
| with EMPG* | 73.7 (+8.1) | 60.8 (+2.6) |
| DAPO* | 80.8 | 73.2 |
| with EMPG* | 88.1 (+7.3) | 73.8 (+0.6) |
| 基线: Qwen2.5-7B-Instruct | ||
| GRPO* | 74.8 | 65.6 |
| with EMPG* | 78.5 (+3.7) | 69.3 (+3.7) |
| DAPO* | 90.0 | 79.6 |
| with EMPG* | 91.6 (+1.6) | 82.7 (+3.1) |
表1:ALFWorld和WebShop任务上的部分性能摘要。EMPG在不同模型和基线上均带来提升。
- 在复杂任务上的可扩展性与泛化能力:在更复杂的Deep Search任务上(见表2),使用Qwen2.5-32B模型,EMPG将DAPO基线的平均分从62.0提升至65.3。尤其值得注意的是,在领域外(OOD)测试集上,EMPG带来的性能增益(+3.9)高于领域内(ID)测试集(+3.1),证明了其优秀的泛化能力。
| 方法 | ID 平均 | OOD 平均 | 总体平均 |
|---|---|---|---|
| Qwen2.5-32B-Instruct | |||
| DAPO (基线) | 63.5 | 59.8 | 62.0 |
| + 梯度缩放 | 63.7 | 63.7 | 63.7 |
| + 未来奖励 | 66.1 | 61.4 | 64.2 |
| + EMPG (本文) | 66.6 (+3.1) | 63.7 (+3.9) | 65.3 (+3.3) |
表2:Deep Search任务上的主要结果和消融研究。
深入分析
-
消融研究:表2的消融实验揭示了EMPG两个组件的互补作用:“未来清晰度奖励”主要提升在训练数据分布内的表现(ID任务),起到了强化利用已知模式的作用;而“自校准梯度缩放”则显著提升了在未知数据上的泛化能力(OOD任务),起到了增强鲁棒性的作用。EMPG整合两者,实现了利用与泛化的协同增益。
-
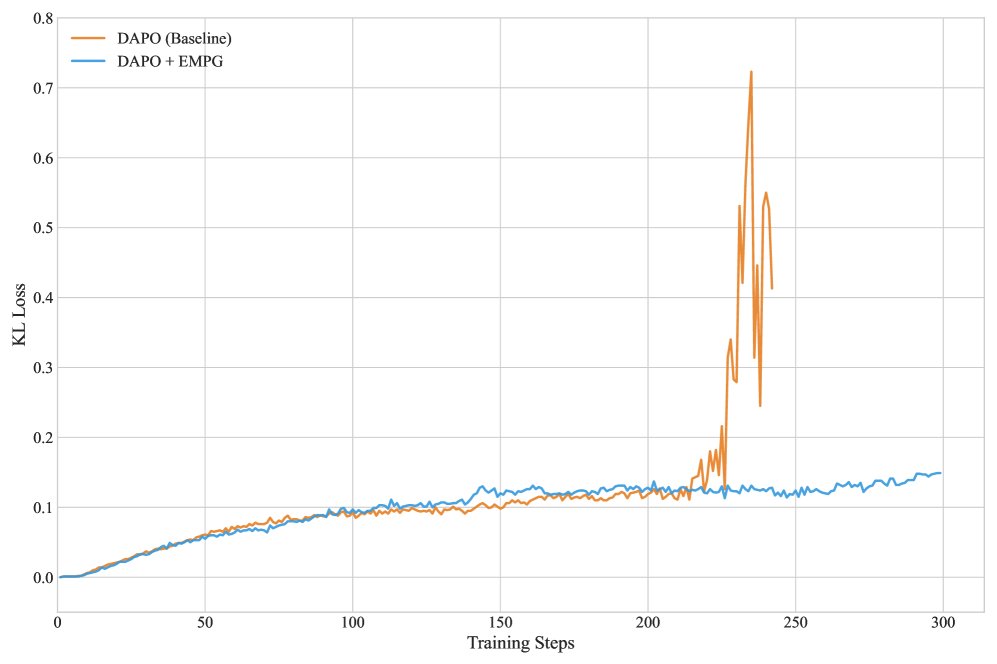
训练稳定性:与基线方法DAPO后期可能出现的“策略崩溃”(KL散度剧烈波动)相比,EMPG在整个训练过程中保持了稳定且较低的KL散度,证明其梯度调制机制有效防止了过度激进的策略更新,确保了训练的稳定收敛。
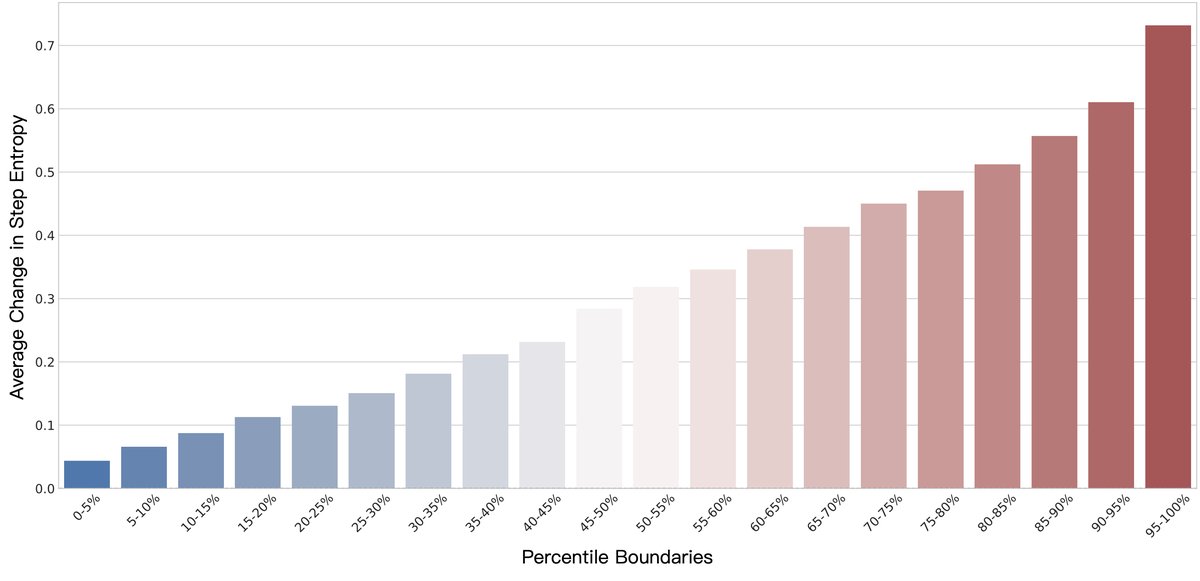
- 步级分析的必要性:分析表明,与之前在token层面的发现不同,在“思考-行动”的步骤层面,即使是初始熵非常低的步骤,在RL微调后其熵值也可能发生巨大变化。这证实了将“步骤”作为分析和调制基本单元的正确性,也是EMPG设计的关键动机。
- 学习动态:实验中的学习曲线显示,基线方法很快会达到性能瓶颈并停滞不前,而EMPG能够持续学习并突破这一瓶颈,最终收敛到更高的性能水平。这表明EMPG不仅是加速学习,更是引导智能体找到了基线方法无法发现的更优策略。
总结
EMPG是一个有理论依据且通用的框架,它通过利用智能体自身的内在不确定性,成功地将稀疏的最终任务奖励转化为了密集、信息丰富且经过校准的步级学习信号。实验证明,该方法在不引入额外标注成本的情况下,显著提升了LLM智能体在长时程任务中的性能、稳定性和泛化能力,为开发更高效、鲁棒的自主智能体奠定了基础。