Imbalanced Gradients in RL Post-Training of Multi-Task LLMs

• ArXiv URL: http://arxiv.org/abs/2510.19178v1

• 作者: Jeongyeol Kwon; Ankur Samanta; Scott Fujimoto; Kaveh Hassani; Yonathan Efroni; Ben Kretzu; Ayush Jain; Runzhe Wu

• 发布机构: Columbia University; Cornell Tech; Meta AI; Meta Superintelligence Labs; Technion

---

TL;DR

本文通过实验证明，在大型语言模型 (LLM) 的多任务强化学习 (RL) 后训练中，不同任务会产生幅度差异悬殊的梯度，并且大梯度并不意味着大的学习增益，这种梯度不平衡现象会导致优化过程偏向特定任务，从而损害整体性能。

关键定义

本文核心关注并揭示了在 LLM 多任务后训练中的一个关键现象：

• 梯度不平衡 (Gradient Imbalance)：在多任务学习中，通过混合数据集进行联合优化时，来自不同任务的梯度在幅度（即范数）上存在巨大差异的现象。当某些任务产生比其他任务大得多的梯度时，模型参数的更新方向将主要由这些“大梯度”任务主导，导致优化资源分配不均，影响小梯度任务的学习。

相关工作

当前，对大型语言模型进行多任务后训练的标准方法是简单地将来自不同任务的数据集合并，然后对模型进行联合优化。这种策略虽然简单，但其背后有一个隐含的假设：即所有任务贡献的梯度幅度大致相似。在计算机视觉等领域，已有研究指出这种梯度不平衡问题，但在大型语言模型领域，尤其是在强化学习后训练的背景下，该问题尚未得到充分探讨。

本文旨在解决的具体问题是：

1. 验证在多任务强化学习后训练 LLM 的过程中，梯度不平衡现象是否确实存在且显著？
2. 探究这种梯度不平衡是否合理，即梯度的大小是否与其对应的学习增益（任务性能提升）正相关？
3. 如果梯度不平衡是有害的，其根本原因是什么？

本文方法

本文的研究方法并非提出一种新的算法，而是一系列旨在揭示、证实和分析“梯度不平衡”现象的诊断性实验。

核心发现：梯度不平衡现象

本文首先通过实验证实了梯度不平衡现象的存在。实验设置涵盖了多个模型（Qwen2.5-3B/7B, Llama-3.2-3B）和两种任务组合：

1. 多领域任务：包括代码生成 (Code)、数学推理 (MATH)、数字构建 (Countdown) 和金融问答 (FinQA)。
2. 单领域（数学）任务：包含三种不同难度的数学任务 (DeepScaleR, MATH, Arithmetic)。

实验采用均匀采样的方式构建批次数据，并追踪了每个任务在训练过程中的平均梯度平方范数。

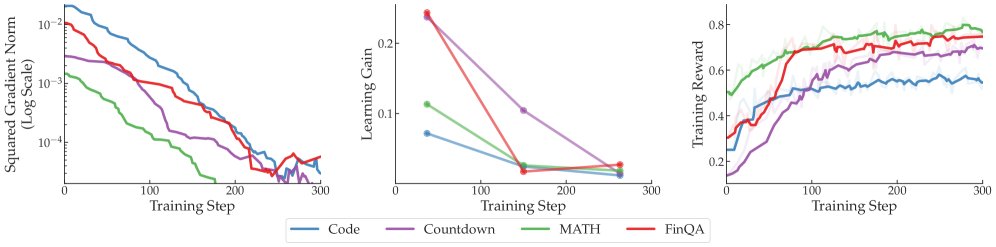
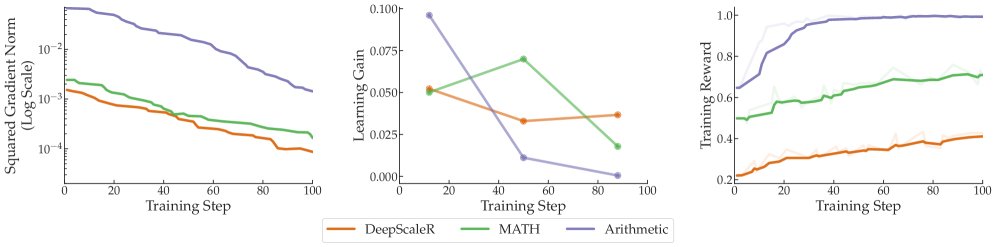
如上图左列所示，实验结果明确显示了梯度的显著不平衡：

• 在多领域设置中，Code 任务的梯度平方范数始终最大，可达 MATH 任务的 15 倍。
• 在单领域（数学）设置中，最简单的 Arithmetic 任务产生的梯度平方范数甚至可达其他数学任务的 33 倍。

这种不平衡导致聚合后的平均梯度被大梯度任务主导，使得优化偏向这些任务。从另一个角度看，这相当于为大梯度任务设置了比小梯度任务高得多的有效学习率，为了维持训练稳定，全局学习率必须调低，这又进一步导致小梯度任务训练不足。

核心论证：梯度与学习增益不相关

梯度不平衡本身不一定有害，如果大梯度能带来大的学习增益，那么这种偏向性反而是有益的。然而，本文通过两种方式证伪了这一假设。

学习增益的量化分析

本文将学习增益定义为训练奖励在一段时间内的变化量：

\[\text{Gain}(t) := \frac{1}{s}\sum_{i=1}^{s}R_{t+i} - \frac{1}{s}\sum_{i=1}^{s}R_{t-i}\]

其中 $R_k$ 是第 $k$ 步的训练奖励。如上图中间列所示，学习增益的模式与梯度幅度的模式完全不同。例如，在多领域任务中，梯度最大的 Code 任务的学习增益却是最低之一；在数学任务中，梯度最大的 Arithmetic 任务在训练后期的学习增益最小。这表明，任务间的梯度差异并不能用学习增益的差异来解释。

梯度比例采样实验

为了进一步验证，本文设计了一种“梯度比例采样”策略，即让梯度更大的任务获得更多的训练机会。其逻辑是：如果大梯度真的意味着大学习潜力，那么优先训练这些任务应该能提升整体平均性能。然而实验结果表明，这种策略并没有带来优势，有时甚至会损害模型的平均性能。这再次证实，跨任务的梯度信号不仅与学习增益不相关，甚至可能产生误导。

来源探究：与其它训练统计量无关

最后，本文探究了其他可能解释梯度不平衡的因素，但均未找到强相关性。

• 优势函数 (Advantage Function)：在策略梯度方法中，梯度公式为 $\nabla_{\theta}J(\theta) = \mathbb{E}[\nabla_{\theta}\log\pi_{\theta}(a\, \mid \,s)A^{\pi}(s,a)]$。理论上，梯度范数受优势函数 $A^{\pi}$ 的绝对值和策略梯度范数 $\ \mid \nabla_{\theta}\log\pi_{\theta}\ \mid $ 的影响。实验分析发现，在单个任务内部，梯度的确与优势函数的绝对值大小有一定正相关性。但跨任务来看，这种关联性消失了，梯度最大的任务（如 FinQA）其优势函数绝对值并不比其他任务高。

  

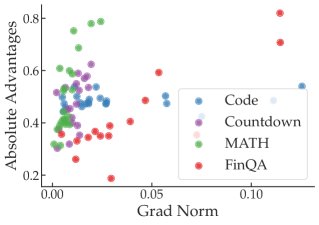
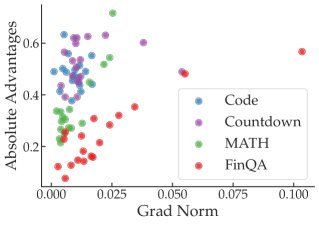
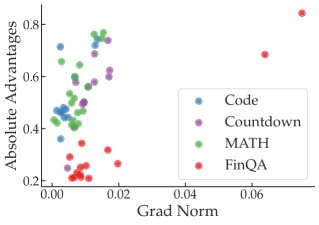
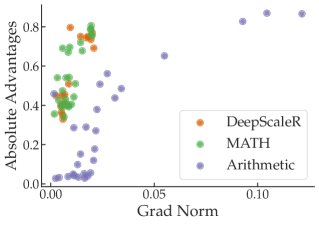
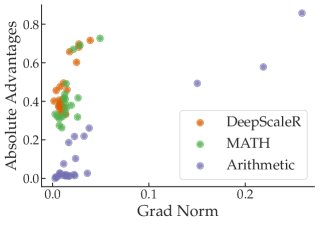
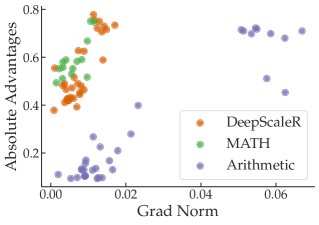
• 训练奖励 (Training Reward)：梯度大小与任务的当前准确率或奖励值之间没有简单的“U型”关系（即在任务太难或太简单时梯度小，在中间难度时梯度大）。

• 提示/响应长度 (Prompt/Response Length)：分析发现，梯度大小与输入提示或模型生成响应的长度之间也没有明显的相关性。

  

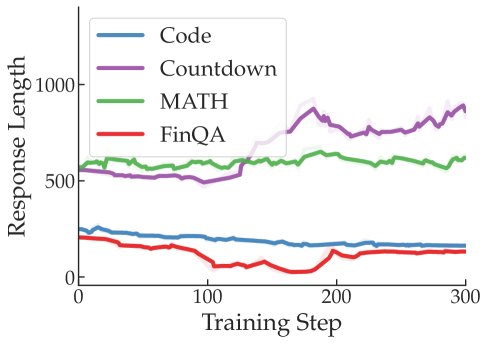
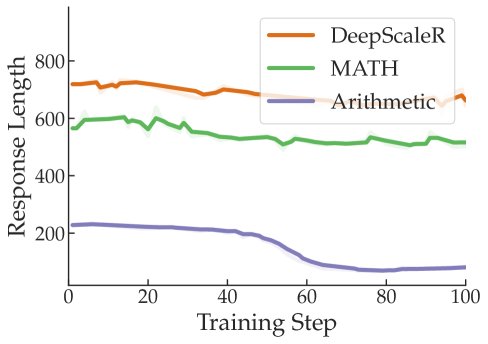
这些分析表明，梯度不平衡并非由训练奖励、优势或序列长度等动态变化的训练统计量所驱动，而更可能源于任务之间的内在差异。

实验结论

• 核心发现：本文的实验有力地证明了在 LLM 的多任务强化学习后训练中，普遍存在严重的梯度不平衡现象。不同任务产生的梯度范数可以相差数十倍。

• 关键验证：梯度不平衡是有害的，因为它与学习增益（即性能提升）之间没有正相关性。梯度最大的任务，其学习潜力并不一定是最大的。实验表明，依据梯度大小来调整任务采样频率的策略，并未能提升模型的整体性能，反而可能造成损害。

• 结论：简单地混合数据集进行多任务联合优化的常用策略存在根本性缺陷。梯度不平衡现象似乎源于任务本身的内在属性，而非简单的训练统计数据可以解释。这警示我们不能再忽视此问题，并呼吁未来的研究应着眼于开发有原则的、在梯度层面进行校正的多任务优化方法。