Improving Online Algorithms via ML Predictions

• ArXiv URL: http://arxiv.org/abs/2407.17712v1

• 作者: Manish Purohit; Ravi Kumar; Zoya Svitkina

• 发布机构: Google

---

TL;DR

本文提出了一种利用机器学习（ML）预测来改进在线算法性能的理论框架，设计的算法在预测准确时性能接近最优（一致性），在预测错误时性能也不会大幅下降，可优雅地退化到经典在线算法的水平（鲁棒性）。

关键定义

本文引入或沿用了以下对理解在线算法与ML预测相结合至关重要的概念：

• 竞争比 (Competitive Ratio)：衡量在线算法性能的标准，定义为在最坏情况输入下，在线算法的成本与知晓所有未来信息的最优离线算法成本的比率。
• 一致性 (Consistency)：衡量当机器学习预测完全准确时，算法性能有多接近最优解。如果一个算法在预测误差为零时的竞争比为 $\beta$，则称其为 $\beta$-consistent。
• 鲁棒性 (Robustness)：衡量在最坏情况下（即预测可能非常糟糕时），算法的性能表现。如果一个算法在任何预测误差下的竞争比都不超过 $\gamma$，则称其为 $\gamma$-robust。
• 预测误差 (Prediction Error, $\eta$)：量化机器学习预测值与真实值之间差距的指标。在本文中，其具体定义与问题相关，例如，对于滑雪租赁问题，$\eta = \mid y-x \mid $（预测天数与真实天数之差的绝对值）；对于作业调度问题，$\eta = \sum_j \mid y_j - x_j \mid $（所有作业预测处理时长与真实时长之差的$L_1$范数）。

相关工作

当前处理不确定性问题主要有两种范式：一是机器学习，通过历史数据构建模型来预测未来；二是在线算法，旨在设计出在最坏情况下性能也有保障的策略，但这种策略往往过于保守，无法利用潜在的有利信息。

近期的研究开始尝试将两者结合，利用ML预测来提升在线算法的性能，核心挑战在于如何设计一种算法，使其：

1. 在预测准确时，能够超越传统在线算法的性能下限（实现良好的一致性）。
2. 在预测错误时，性能不至于崩溃，至少能维持传统在线算法的水平（保证鲁棒性）。

本文旨在为两个经典的在线问题——滑雪租赁和非预知型作业调度——设计出兼具一致性和鲁棒性的新算法。

本文方法

本文的核心思想是：不盲目信任ML预测，而是将其作为调整经典在线算法决策策略的依据，通过引入一个超参数 $\lambda$ 来平衡对预测的信任程度和对最坏情况的防范。

滑雪租赁问题 (Ski Rental)

问题背景：每天租滑雪板花费1单位，一次性购买花费 $b$ 单位。滑雪者不知道总共会滑雪多少天（真实天数 $x$），但有一个ML模型预测的天数 $y$。

朴素算法的缺陷

一个简单的想法是完全信任预测：若 $y \geq b$，则第一天就买；否则一直租。该算法（Algorithm 1）在预测准确时（$\eta=0$）成本最优，是1-consistent的。但若预测严重失误（例如预测天数很少 $y < b$，实际天数很多 $x \gg b$），其成本会无限高，因此不具备鲁棒性。

确定性鲁棒且一致的算法 (Algorithm 2)

为解决上述问题，本文提出了一种引入超参数 $\lambda \in (0, 1)$ 的确定性算法：

• 如果预测 $y \geq b$ （倾向于买），则在第 $\lceil\lambda b\rceil$ 天购买。
• 如果预测 $y < b$ （倾向于租），则在第 $\lceil b/\lambda\rceil$ 天购买。

创新点：此算法通过 $\lambda$ 在信任预测和保守策略之间取得平衡。

• 优点：当 $\lambda \to 0$ 时，算法更信任预测，一致性更好（趋近于1）；当 $\lambda \to 1$ 时，算法更保守，鲁棒性更好（趋近于经典的最优确定性算法，竞争比为2）。该算法是 $(1+1/\lambda)$-robust 和 $(1+\lambda)$-consistent 的，提供了一个平滑的权衡。

随机化鲁棒且一致的算法 (Algorithm 3)

为获得更好的性能权衡，本文进一步设计了一种随机化算法。该算法不再在固定的某一天购买，而是在一个时间窗口内，根据一个特定的概率分布随机选择一天购买。

• 如果预测 $y \geq b$，则在 ${1, \dots, \lfloor\lambda b\rfloor}$ 天内根据概率分布 $q_i$ 随机选择购买日。
• 如果预测 $y < b$，则在 ${1, \dots, \lceil b/\lambda\rceil}$ 天内根据概率分布 $r_i$ 随机选择购买日。

创新点：通过随机化，该算法平滑了决策的“尖锐性”，避免了在某个特定决策点被对手（adversary）针对。

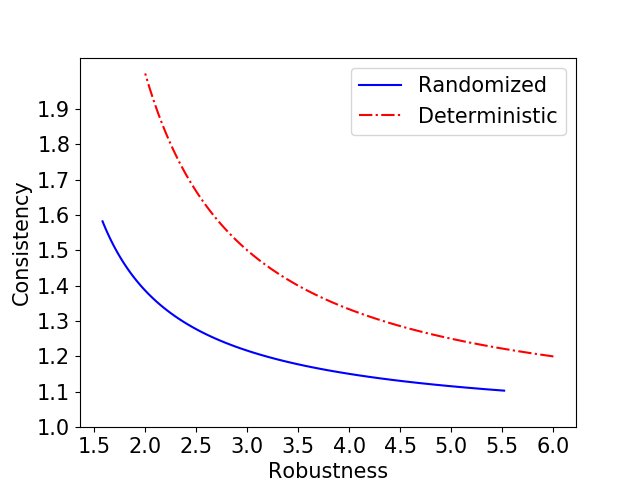
• 优点：该算法是 $(\frac{1+1/b}{1-e^{-(\lambda-1/b)}})$-robust 和 $(\frac{\lambda}{1-e^{-\lambda}})$-consistent 的。如下图所示，与确定性算法相比，它在相同的鲁棒性保证下，能提供更好的一致性。

非预知型作业调度问题 (Non-clairvoyant Job Scheduling)

问题背景：在单台机器上调度 $n$ 个作业，目标是最小化总完成时间。作业的实际处理时间 $x_j$ 未知，但有预测值 $y_j$。可随时抢占和恢复作业。经典的最优非预知算法是轮询（Round-Robin, RR），竞争比为2。

偏好轮询算法 (Preferential Round-Robin, PRR)

本文提出的PRR算法结合了两种策略：

1. 按预测最短作业优先 (Shortest Predicted Job First, SPJF)：按预测处理时间 $y_j$ 从小到大依次执行作业。此策略一致性好但鲁棒性差。
2. 轮询 (Round-Robin, RR)：平均分配CPU时间给所有未完成的作业。此策略鲁棒性好（竞争比为2）。

PRR算法以 $\lambda$ 的速率执行SPJF策略，同时以 $1-\lambda$ 的速率执行RR策略。具体来说，在任何时刻，当前“预测最短”的未完成作业获得 $\lambda$ 的处理速率，同时所有未完成的作业分享剩下的 $1-\lambda$ 的处理速率。

创新点：该算法是一种混合策略，通过一个参数 $\lambda$ 融合了一个基于预测的高性能策略和一个保证最坏情况的经典策略。

• 优点：PRR算法是 $(\frac{2}{1-\lambda})$-robust 和 $(\frac{1}{\lambda})$-consistent 的（在更精确分析下，对于 $\eta=0$ 的情况，一致性可达 $\frac{1+\lambda}{2\lambda}$）。这使得算法在预测准确时性能远超RR，在预测错误时性能不低于RR，成功地利用了预测信息同时规避了其带来的风险。

实验结论

本文通过模拟实验验证了所提出算法的有效性。

滑雪租赁实验

• 设置：购买成本 $b=100$，真实天数 $x$ 在 $[1, 400]$ 之间均匀采样，预测误差服从均值为0、标准差为 $\sigma$ 的正态分布。
• 结论：如下图(a)所示，即使在预测误差较大时（例如 $\sigma = 2b$），本文提出的使用预测的算法（确定性和随机化）的平均竞争比也显著优于不使用预测的经典算法。特别是，本文的确定性算法表现甚至优于经典的随机化算法。

非预知型调度实验

• 设置：50个作业，其处理时间从帕累托分布（Pareto distribution）中采样，统计数据如下表所示。预测误差同样服从正态分布。

N	min	max	mean	$\sigma$
50	1	22352	2168	5475.42

• 结论：如下图(b)所示，单纯依赖预测的SPJF算法在误差增大时性能急剧下降。而本文提出的PRR算法（$\lambda=0.5$）在预测准确时性能远好于RR，而在预测误差很大时，其性能也能稳定在RR的水平，表现出很好的鲁棒性。

(a) 滑雪租赁

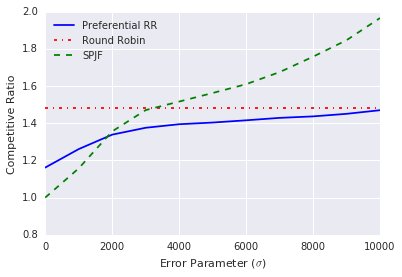(b) 非预知型调度

最终结论：实验结果有力地支持了理论分析，证明了本文提出的算法框架能够在实际中有效利用机器学习预测来提升在线决策的性能，同时保持了必要的安全保障。