Inpainting-Guided Policy Optimization for Diffusion Large Language Models

ArXiv URL: http://arxiv.org/abs/2509.10396v1
作者: Siyan Zhao; Bo Liu; Mengchen Liu; Aditya Grover; Yuandong Tian; Guan Pang; Feiyu Chen; Miao Liu; Chenyu Wang; Jing Huang; 等11人
发布机构: MIT; Meta Superintelligence Labs; Tsinghua University; UCLA

TL;DR

本文提出了一种名为 IGPO (Inpainting-Guided Policy Optimization) 的强化学习框架，它利用扩散大语言模型 (dLLM) 独特的“填补” (inpainting) 能力，通过在探索过程中策略性地注入部分真实推理线索，从而有效解决强化学习中的探索效率低下和零优势困境问题。

关键定义

掩码扩散大语言模型 (Masked Diffusion Large Language Models, dLLMs)：一种非自回归的语言模型，它通过一个逐步去噪（或去掩码）的过程并行生成文本。与从左到右生成的自回归模型不同，dLLMs 能够基于双向上下文进行生成，并天然支持对文本中间部分进行内容填补（inpainting）。
填补 (Inpainting)：dLLMs 的一种核心能力，指在给定部分上下文（例如，一段文本的开头和结尾，或中间的某些片段）的情况下，填充缺失内容。本文利用此能力，将真实的推理步骤片段作为“提示”注入生成过程，以引导模型探索。
零优势困境 (Zero-Advantage Dilemma)：在基于组的策略优化方法（如 GRPO）中，当一个组内所有采样的回答都获得相同的奖励（例如全错或全对）时，计算出的优势值（Advantage）全部变为零。这导致策略梯度也为零，无法产生有效的学习信号，造成计算资源的浪费。
IGPO (Inpainting-Guided Policy Optimization)：本文提出的核心框架。当检测到“零优势困境”（特指全错情况）时，IGPO会触发填补机制：它将真实解题步骤分块，随机注入一部分作为固定提示，让 dLLM 完成剩余的推理。通过用这些成功生成的回答替换部分错误回答，IGPO人为地在采样组中创造了奖励差异，从而恢复了有效的梯度信号。
长度对齐的监督微调 (Length-Aligned Supervised Fine-tuning, SFT)：本文提出的一种辅助训练策略。由于 dLLM 在线强化学习的计算成本高，通常生成长度受限。该策略通过将冗长的原始推理文本重写为简洁版本，使得SFT阶段的训练数据长度与后续RL和评估阶段的生成长度保持一致，为RL提供了一个更强的初始化模型。

本文方法

IGPO: Inpainting-Guided Policy Optimization

创新点

本文的核心创新是 IGPO，第一个利用 dLLM 的填补能力来指导强化学习过程的框架。它通过在采样过程中有条件地注入部分真实解题线索，巧妙地解决了探索难题和零优势困境。

核心机制

IGPO 的设计旨在应对 GRPO 中的“零优势困JE”。当模型为一个问题生成的一组（例如G个）回答全部错误时，优势值为零，梯度消失，公式如下：

\[\nabla_{\theta} \mathcal{L}(\theta) = \mathbb{E}\left[\frac{1}{G} \sum_{i=1}^{G} \frac{1}{ \mid o_i \mid } \sum_{k=1}^{ \mid o_i \mid } A_i \, \rho_i^k \, \nabla_{\theta} \log \pi_{\theta}(o_i^k \mid q)\right] = 0, \quad \text{当 } A_i=0 \tag{5}\]

为解决此问题，IGPO引入了弹性填补触发采样 (Elastic Inpainting-Triggered Sampling) 机制，如下图所示。

图 2: IGPO 概览。当采样组内所有回答都错误时（零优势场景），通过注入真实推理片段作为提示来引导填补生成。这些成功的填补生成结果将替换掉部分原始错误回答，从而创造奖励差异，使策略梯度更新成为可能。

具体步骤如下：

触发条件：仅当采样组内所有回答 $o_i$ 的奖励 $r(o_i)$ 均为 0 时，激活 IGPO。
提示构建：将真实的推理过程 $y^*$ 分割成多个连续的文本块 $c_j$。
提示注入与填补：随机选择一部分文本块（根据注入比例 $\eta$），将其作为固定的“提示”嵌入到待生成的序列中。dLLM 利用其双向注意力机制，在“填补”模式下生成剩余的掩码部分。注入提示的初始序列 $z^{\text{hint}}$构造如下：

\[z^{\text{hint}}[i] = \begin{cases} y^*[i] & \text{if } m[i] = 1 \text{ and } i \le \mid y^* \mid , \\ \text{mask} & \text{otherwise.} \end{cases} \tag{6}\]

样本替换：生成一组新的、经过填补引导的回答 ${\tilde{o}_i}$。检验其正确性，并将其中成功的回答替换掉原始“全错组”中的一部分样本（替换比例由 $\lambda$ 控制）。
梯度恢复：经过替换后，新的样本组包含了奖励为1（成功）和0（失败）的回答，从而打破了零优势僵局，产生了有意义的非零优势值，使得策略可以正常更新。

完整的 IGPO 算法流程如下：

算法 1: IGPO - 用于掩码 dLLM 的填补引导策略优化
需要: 参考模型 $\pi_{\text{ref}}$, 提示分布 $\mathcal{D}$, 真实推理轨迹 ${y^*}$, 每个提示的完成数 $G$, 内部更新次数 $\mu$, 提示注入比例范围 $[\eta_{\text{low}}, \eta_{\text{high}}]$, 替换分数 $\lambda$, 熵过滤器阈值 $\tau$, 块大小范围 $[s_{\min}, s_{\max}]$
1: 初始化 $\pi_{\theta} \leftarrow \pi_{\text{ref}}$
2: while 未收敛 do
3: $\pi_{\text{old}} \leftarrow \pi_{\theta}$
4: 采样提示 $q \sim \mathcal{D}$ 和 G 个响应 $o_i \sim \pi_{\text{old}}(\cdot \mid q), i \in [G]$ 并计算奖励 $r_i$
5: if 所有 $r_i = 0$ (零优势情况) then
6: 将真实推理 $y^*$ 分割成块 ${c_1, \ldots, c_N}$，其中 $ \mid c_j \mid \sim \mathcal{U}[s_{\min}, s_{\max}]$
7: for $i=1,\ldots,G$ do
8: 采样提示注入比例 $\eta \sim \mathcal{U}[\eta_{\text{low}}, \eta_{\text{high}}]$ 并随机选择 $\lfloor \eta N \rfloor$ 个块
9: 将选定块的 token 作为固定提示注入相应位置
10: 通过填补生成 $\tilde{o}_i$：迭代去噪剩余的掩码位置，同时保持提示 token 不变
11: 评估奖励 $r(\tilde{o}_i)$，并用填补生成的正确响应替换最多 $\lfloor \lambda G \rfloor$ 个错误响应
12: 使用 Eq. 3 在更新后的响应集上计算优势 $A_i^k$
13: for $n=1,\ldots,\mu$ do
14: 估计 $\pi_{\theta}, \pi_{\text{old}}, \pi_{\text{ref}}$ 下的对数概率
15: 对于提示 token 位置，仅更新熵值最高的 top-$\tau$ 百分位的 token
16: 通过 $\mathcal{L}_{IGPO}(\theta)$ (Eq. 7) 更新 $\pi_{\theta}$
17: return $\pi_{\theta}$

优点

缓解分布失配：与完全依赖真实数据进行监督学习（SFT）不同，IGPO 仅注入部分提示，大部分内容仍由模型自行生成。这使得学习信号更接近模型当前的策略分布（on-policy），缓解了 SFT 中训练与推理分布不一致的问题。它巧妙地在 SFT 和 RL 之间架起了一座桥梁。
稳定训练过程：为了处理注入的真实 token（来自外部数据分布）可能带来的训练不稳定性，本文提出了基于熵的梯度过滤 (Entropy-based Gradient Filtering)。对于被注入的提示 token，只在模型本身不确定性较高（即熵值较高）的位置进行梯度更新。这避免了强制模型在它已经很自信的位置上进行突兀的改变，从而使训练更加稳定。

长度对齐的 SFT

背景与动机

像 LLaDA 这样的全注意力 dLLM 计算成本高昂，尤其是在线 RL 训练时。这迫使研究者在 RL 阶段使用较短的生成序列（如256个token）。然而，许多用于SFT的推理数据集（如OpenR1）包含非常冗长的推理过程（超过10k个token）。直接在这些长文本上进行SFT，会导致模型在SFT阶段和RL阶段看到的序列长度严重不匹配，影响了RL的初始性能。

方法与优点

为解决该问题，本文提出了一种通过重写推理轨迹实现长度对齐的SFT策略：

重写：使用强大的教师模型（LLaMA-4-Maverick）将原始数据集中冗长、重复的推理过程，系统性地重写为简洁、结构化的版本，同时保留核心逻辑。
对齐：在这些重写后的、长度更短的轨迹上进行 SFT。

这种方法使得 SFT 阶段的训练数据分布与 RL 阶段的生成约束更加匹配，为后续的 RL 训练提供了一个质量更高、更适应任务的初始模型，让模型可以在有限的计算预算内专注于提升推理质量，而非学习如何压缩文本。

实验结论

图 1 (b)：IGPO 显著减少了“全错组”的出现频率。

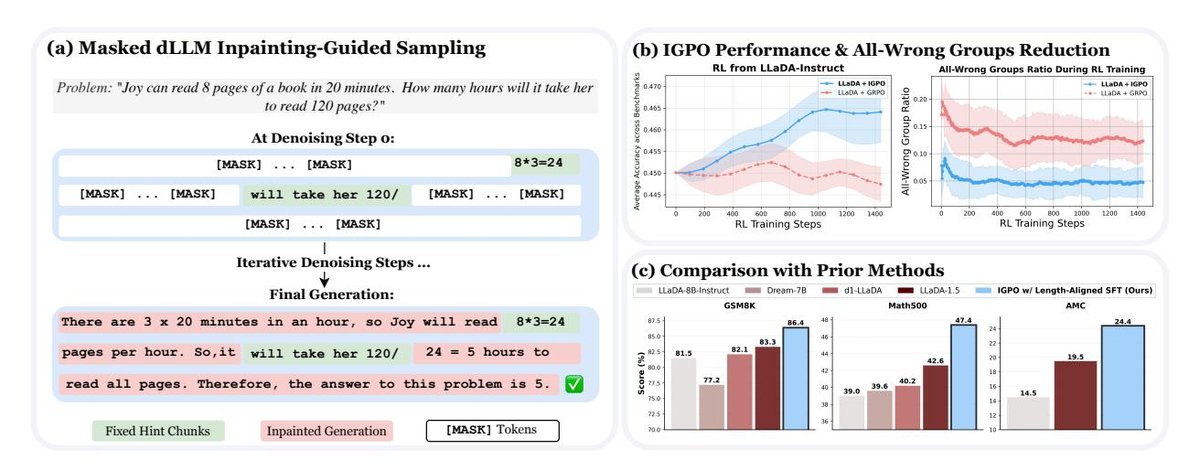图 1 (c)：结合长度对齐SFT和IGPO的完整训练流程在三大数学基准测试中取得了SOTA性能。

本文通过在 LLaDA-8B 模型上的一系列实验，验证了所提方法的有效性。

主要结果

性能显著提升：如表1 所示，完整的训练流程（长度对齐SFT + IGPO）在多个数学推理基准上取得了巨大成功。相较于 LLaDA-Instruct 基线模型，GSM8K 提升了 4.9%，MATH500 提升了 8.4%，AMC 提升了 9.9%。这使得模型在全注意力掩码 dLLM 中达到了新的 SOTA 水平。

表1: 在多个数学任务上的性能表现。

模型	GSM8K (pass@1)	MATH500 (pass@1)	AMC (avg@16)	平均
…（其他模型）…
LLaDA-Instruct (基线)	81.5 (+0)	39.0 (+0)	$14.5_{(+0)}$	$45.0 \ (+0)$
LLaDA-Instruct + IGPO (本文)	$\underline{83.6} \ (+2.1)$	$\underline{42.8}_{(+3.8)}$	$\underline{18.1}_{(+3.8)}$	$\underline{48.2}$ (+3.2)
LLaDA-Instruct + 长度对齐 SFT (本文)	$83.6_{(+2.1)}$	$45.2_{(+6.2)}$	22.3 (+7.8)	$50.4_{(+5.4)}$
LLaDA-Instruct + 长度对齐 SFT + IGPO (本文)	$\underline{\textbf{86.4}}_{(+4.9)}$	$\underline{47.4}_{(+8.4)}$	$\underline{24.4}_{(+9.9)}$	$\underline{52.7}_{(+7.7)}$

训练更稳定、高效：如图3 所示，无论是否经过 SFT，IGPO 的训练曲线都比标准的 GRPO 更加平滑和稳定。实验表明，IGPO 将“全错组”的比例降低了约 60%（如图1(b)所示），这直接转化为更有效的梯度更新和更高的样本效率。

图 3: IGPO 与标准 GRPO 训练曲线对比。无论从哪个检查点开始，IGPO 都展现出更优越和稳定的训练性能。

消融分析

部分填补优于完全填补：图4 显示，注入部分提示（例如注入比例在0.2-0.6之间）的效果优于注入完整的真实答案（注入比例为1.0）。这证实了 IGPO 的核心思想：引导而非替代。通过让模型在提示之间进行自我推理和连接，产生的学习信号更接近模型自身的能力边界，比单纯的监督学习更有效。

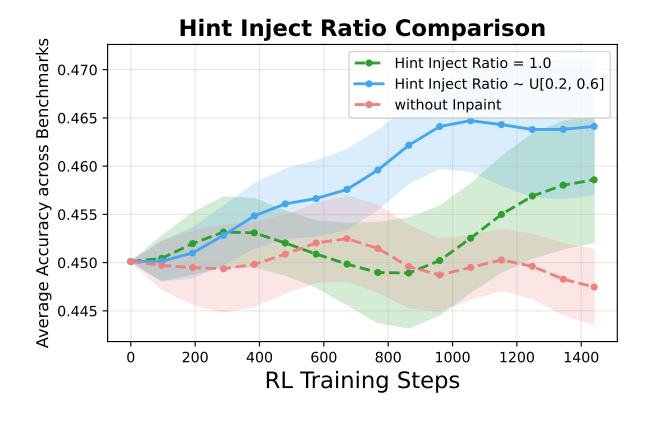图 4: 不同提示注入比例对性能的影响。部分注入始终优于完全注入。

熵过滤是稳定训练的关键：图5 表明，对注入的提示 token 进行熵过滤至关重要。只在熵值最高的 20% 的位置进行梯度更新（$\tau=0.2$）时，性能最好且训练最稳定。如果不进行过滤（$\tau=1.0$），训练会出现剧烈波动，证明了该机制在融合异构数据源时的必要性。

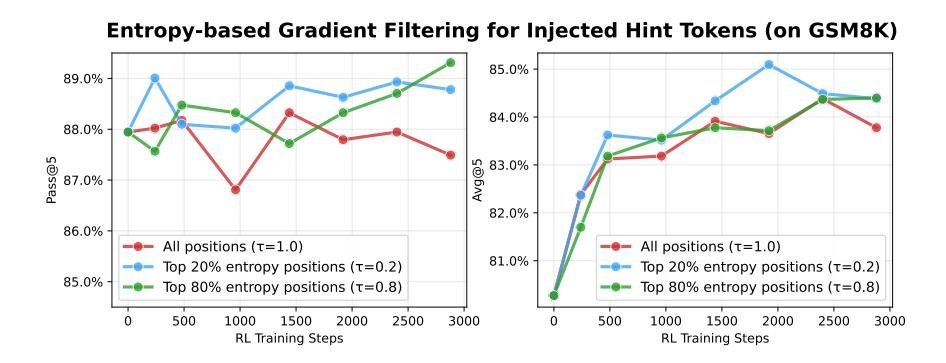图 5: 熵剪裁阈值对提示 token 的影响。$\tau=0.2$ 表现最佳。

重写推理轨迹的有效性：图6 证明了“长度对齐SFT”的价值。使用重写后的简洁轨迹进行 SFT，不仅直接提升了 SFT 后的模型性能，也为后续 RL 训练提供了更好的起点，最终获得了更高的准确率。同时，无论在哪种 SFT 初始化的模型上，IGPO 都比标准 RL 表现更优，尤其是在保持生成多样性方面。

图 6: SFT 和 RL 中使用重写轨迹与原始轨迹的对比。重写轨迹带来了更高的SFT性能和最终的RL准确率。

总结

实验结果有力地证明，IGPO 及其配套的长度对齐SFT策略构成了一套极为有效的 dLLM 训练方案。该方法不仅通过利用 dLLM 的独特能力解决了强化学习中的关键瓶颈（探索效率和零优势困境），还在多个数学推理任务上取得了SOTA性能，为非自回归模型的进一步发展和应用开辟了新道路。