iTransformer: Inverted Transformers Are Effective for Time Series Forecasting
-
ArXiv URL: http://arxiv.org/abs/2310.06625v4
-
作者: Yong Liu; Haoran Zhang; Shiyu Wang; Mingsheng Long; Lintao Ma; Tengge Hu; Haixu Wu
-
发布机构: Ant Group; Tsinghua University
TL;DR
本文提出iTransformer,通过将Transformer的输入维度进行“反转”,即视每个单独的时间序列变量为一个独立的Token,从而使自注意力机制能够有效捕捉多变量间的相关性,而前馈网络则用于学习每个序列的非线性表示,最终显著提升了时间序列预测的性能和泛化能力。
关键定义
- 时间Token (Temporal Token):传统Transformer预测模型中的基本单元。它由同一时间戳下的多个变量(variates)的观测值组成,模型通过对这些时间Token序列应用注意力机制来捕捉时间依赖关系。
- 变量Token (Variate Token):iTransformer提出的核心概念。它将每个独立的变量在整个回看窗口(lookback window)内的完整时间序列作为一个Token。这使得模型处理的基本单元从“时间切片”转变为“变量序列”。
- 维度反转 (Inverted Dimensions):本文的核心思想。指的是将传统Transformer在时间维度上应用自注意力(Self-Attention)、在特征维度上应用前馈网络(FFN)的做法,反转为在变量(variate)维度上应用自注意力、在时间序列表示上应用前馈网络。
相关工作
当前,基于Transformer的时间序列预测模型通常将每个时间点上的多变量数据捆绑成一个“时间Token”,并在此序列上应用注意力机制。然而,这一范式面临诸多挑战:
- 性能瓶颈:随着回看窗口的增大,模型性能反而下降,且计算复杂度急剧增加。
- 表征谬误:将具有不同物理意义和延迟事件的多个变量强行融合到一个时间Token中,可能导致无法学到以变量为中心的有效表示,产出无意义的注意力图。
- 范式质疑:近期研究发现,一些简单的线性模型在多个基准测试上其性能和效率甚至超越了复杂的Transformer模型,这引发了对Transformer在时间序列领域适用性的根本性质疑。
此外,现有模型大多难以在不改变Transformer原生组件的情况下,有效建模多变量之间的相关性。
本文旨在解决上述问题,即传统Transformer架构在多变量时间序列预测任务中的不适应性。作者认为问题不在于Transformer本身无效,而在于其使用方式不当。
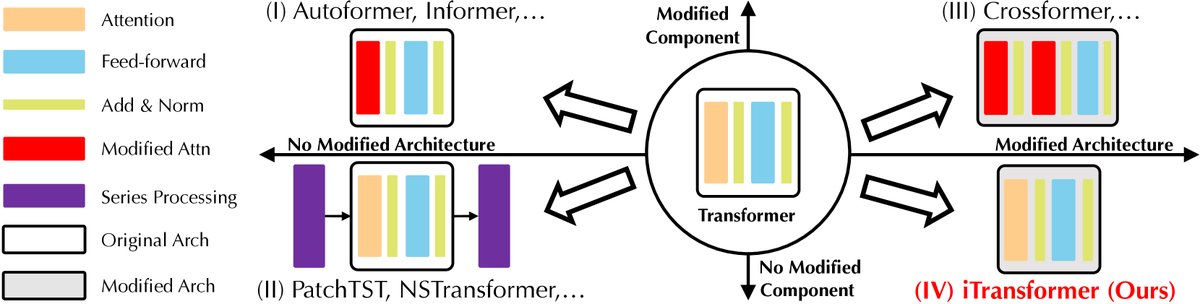
图:根据对组件和架构的修改对基于Transformer的预测器进行分类。iTransformer属于第四类,即不修改组件,但改变其作用维度和架构。
本文方法
本文提出的iTransformer通过反转Transformer组件的作用维度,重新定义了其在时间序列预测中的角色,采用了一个简洁的仅编码器 (encoder-only) 架构。
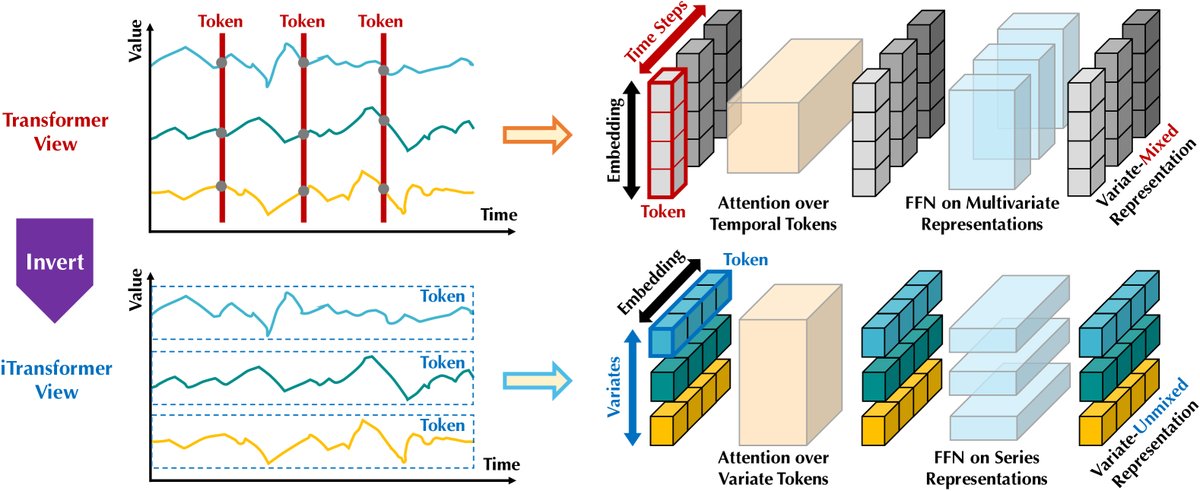
图:Vanilla Transformer将每个时间步的数据作为Token;iTransformer则将每个变量的完整序列作为Token,使注意力机制捕捉变量间相关性,前馈网络学习序列表示。
架构创新:维度反转
iTransformer的核心是将输入数据的处理维度进行了反转。对于一个包含\(N\)个变量和\(T\)个时间步的输入\(\mathbf{X} \in \mathbb{R}^{T \times N}\),其处理流程如下:
-
序列化Token嵌入 (Embedding):每个变量的完整时间序列 $\mathbf{X}_{:,n}$(长度为\(T\))被独立地通过一个MLP嵌入成一个“变量Token” $\mathbf{h}_n \in \mathbb{R}^{D}$。这样,输入就从一个时间序列矩阵变为一个由\(N\)个变量Token组成的序列 $\mathbf{H} \in \mathbb{R}^{N \times D}$。
-
反转的Transformer模块:模型由多个堆叠的Transformer模块构成,但其内部组件的作用被重新定义。
-
层归一化 (Layer Normalization):对每个变量Token $\mathbf{h}_n$ 单独进行归一化。这有助于处理不同变量因单位、尺度不同导致的分布差异(即非平稳性),避免了传统方法中在时间步维度上归一化可能造成的过平滑问题。 $$ \operatorname{LayerNorm}(\mathbf{H})=\left{\frac{\mathbf{h}{n}-\operatorname{Mean}(\mathbf{h}{n})}{\sqrt{\operatorname{Var}(\mathbf{h}_{n})}}\bigg{ } n=1,\dots,N\right} $$ -
自注意力机制的角色转变 (Self-Attention):自注意力机制被应用于\(N\)个变量Token之间。其计算的注意力分数矩阵 $\mathbf{A} \in \mathbb{R}^{N \times N}$ 直接反映了变量与变量之间的相关性。这使得注意力图具有了清晰的物理解释性,帮助模型关注与预测目标最相关的其他变量。
- 前馈网络的角色转变 (Feed-Forward Network):前馈网络(FFN)被独立且共享地应用于每一个变量Token。由于每个Token代表一个完整的序列,FFN在此处的作用是学习复杂的、非线性的时间序列表示。它负责提取如周期性、趋势性等序列内在模式,其作用类似于近期表现优异的纯MLP模型。
-
-
预测输出 (Projection):经过\(L\)层Transformer模块处理后,最终的变量Token表示 $\mathbf{h}_n^L$ 被送入一个线性投影层,直接生成对该变量未来\(S\)个时间步的预测值 $\hat{\mathbf{Y}}_{:,n}$。
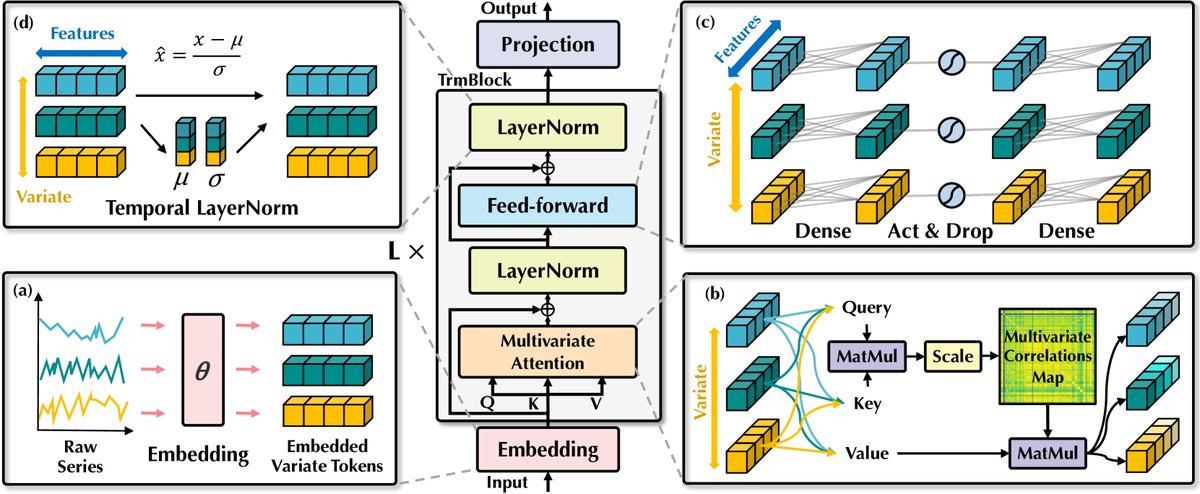
图:iTransformer整体架构图。展示了序列嵌入、自注意力、前馈网络和层归一化的反转应用。
优点
- 保留变量特性:将每个变量视为独立Token,避免了不同物理意义的变量在输入端被强制混合,保留了各自的独特性。
- 可解释性强:自注意力机制直接建模变量间的相关性,其注意力图直观易懂。
- 发挥组件优势:充分利用了FFN在学习单序列非线性模式上的强大能力,并让注意力机制专注于其更擅长的关系建模。
- 解决性能瓶颈:模型性能随回看窗口增大而提升,克服了传统Transformer的缺陷。
- 泛化能力强:模型对变量数量具有灵活性,能够很好地泛化到训练中未见过的变量,为构建时间序列基础模型提供了可能。
实验结论
iTransformer在多个真实世界数据集上的实验表现优异,验证了其设计的有效性。
核心性能
- SOTA结果:在ECL、ETT、Traffic、PEMS等7个基准数据集上,iTransformer全面超越了包括PatchTST、DLinear在内的10个先进基线模型,取得了当前最佳(SOTA)性能,尤其在高维数据集上优势明显。
| 模型 | iTransformer (Ours) | RLinear (2023) | PatchTST (2023) | TimesNet (2023) | DLinear (2023) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 指标 | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
| ECL | 0.178 | 0.270 | 0.219 | 0.298 | 0.205 | 0.290 | 0.192 | 0.295 | 0.212 | 0.300 |
| ETT (Avg) | 0.383 | 0.399 | 0.380 | 0.392 | 0.381 | 0.397 | 0.391 | 0.404 | 0.442 | 0.444 |
| Traffic | 0.428 | 0.282 | 0.626 | 0.378 | 0.481 | 0.304 | 0.620 | 0.336 | 0.625 | 0.383 |
| Weather | 0.258 | 0.278 | 0.272 | 0.291 | 0.259 | 0.281 | 0.259 | 0.287 | 0.265 | 0.317 |
| PEMS (Avg) | 0.119 | 0.218 | 0.514 | 0.482 | 0.217 | 0.305 | 0.148 | 0.246 | 0.320 | 0.394 |
表1:多变量预测结果摘要(MSE/MAE,越低越好),iTransformer在多数数据集上表现最佳。
框架泛化性与优势验证
- 普适性提升 (iTransformers):将“维度反转”思想应用于多种Transformer变体(如Reformer, Informer, FlashAttention),其性能均获得巨大提升(平均MSE降低16.8%至38.9%),证明了该框架的普适性和有效性。
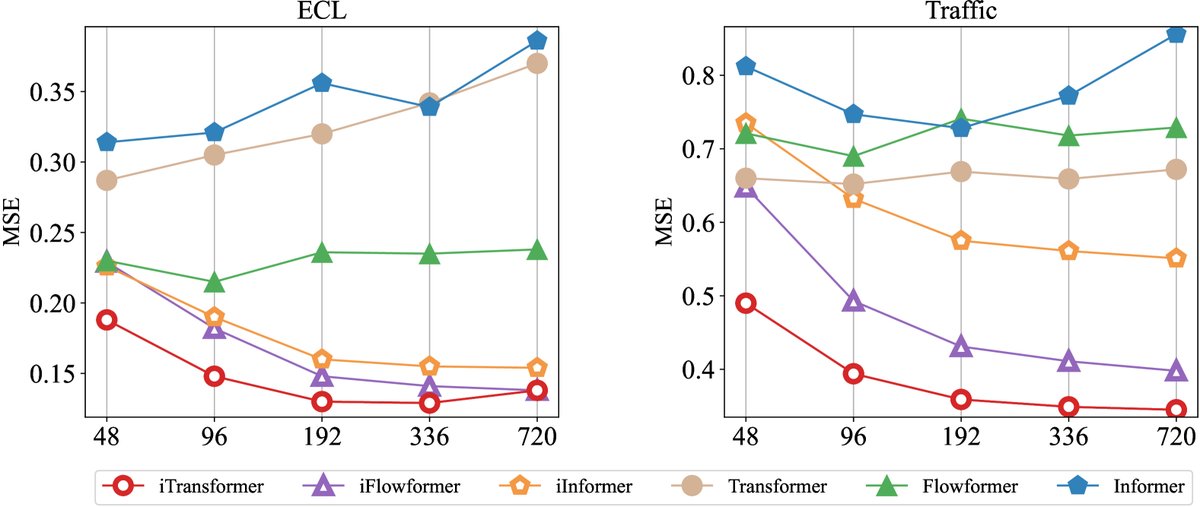
图:与传统Transformer不同,iTransformer及其变体的性能随回看窗口长度的增加而稳定提升。
-
长回看窗口优势:实验证明,iTransformer的预测精度随回看窗口(lookback length)的增长而持续提高,解决了传统Transformer模型在此问题上的性能退化现象。
-
变量泛化能力:在仅用20%的变量进行训练,再对全部变量进行预测的“零样本”场景下,iTransformer表现出很强的泛化能力,性能下降幅度远小于传统的通道独立(Channel Independence)方法。
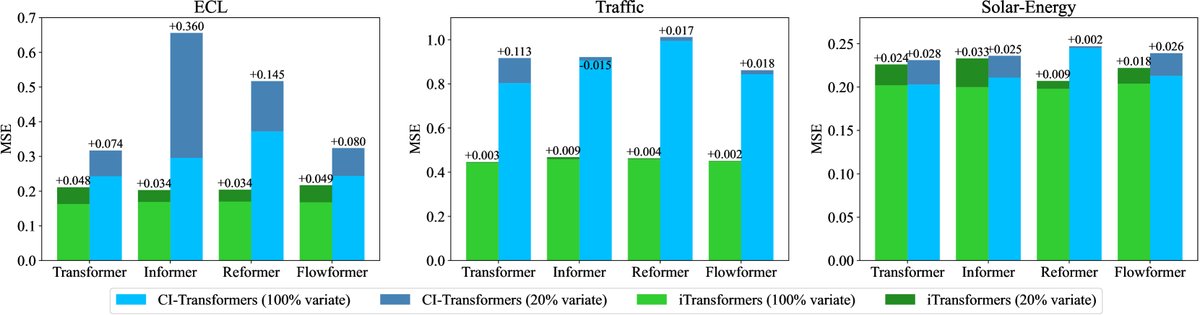
图:在仅用部分变量训练的泛化测试中,iTransformer(橙色)相比基线(蓝色)性能下降更少,展现了更强的泛化能力。
模型分析
- 消融研究:实验验证了“注意力用于变量维度、FFN用于时间维度”是最佳组合。若对调两者作用或移除任一组件,性能均会显著下降,其中传统Transformer的架构(FFN作用于变量,注意力作用于时间)表现最差。
- 表征分析:通过CKA相似度分析发现,iTransformer在不同层之间学习到的表示更加一致,这与时间序列预测任务中更好的性能相关。同时,注意力图的可视化也证实了其能有效捕捉变量间的真实相关性。
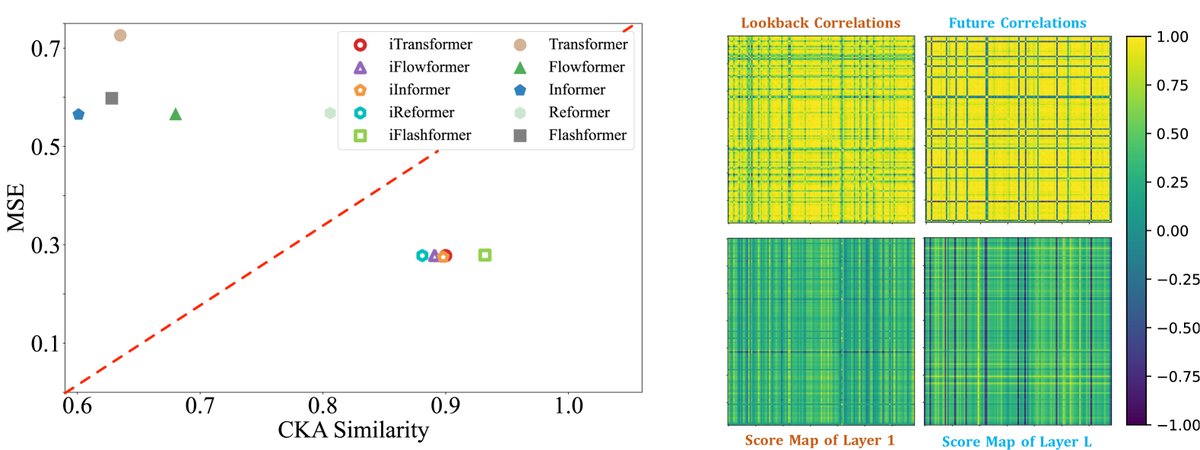
图:左侧显示iTransformer(绿色三角)具有更高的CKA相似度和更低的MSE。右侧显示iTransformer的注意力图能从原始数据相关性(浅层)演化为未来数据相关性(深层)。
- 高效训练策略:本文提出一种高效训练策略,即在每个batch中随机采样部分变量进行训练。该方法可在大幅降低显存占用的同时,基本不影响最终的预测性能。
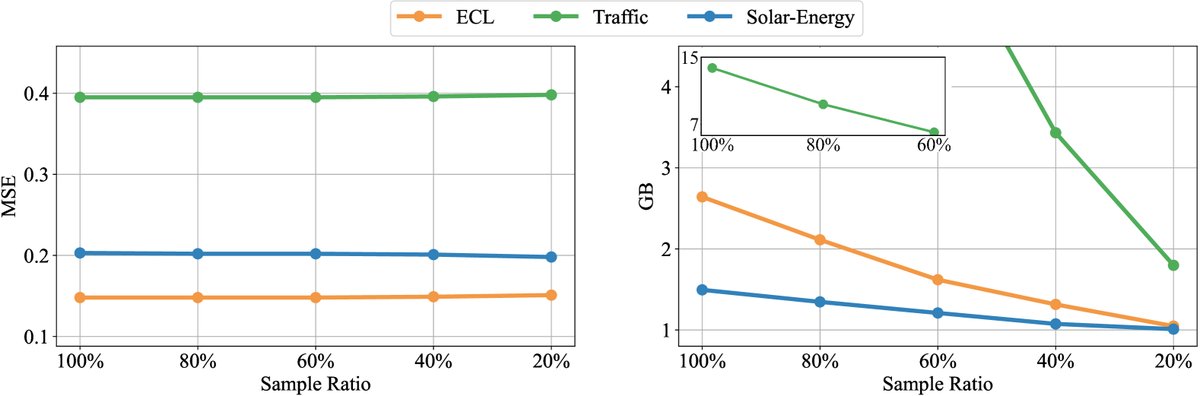
图:随着采样变量比例的降低,模型性能(左)保持稳定,而显存占用(右)显著减少。
最终结论
本文成功证明了,通过简单而深刻的“维度反转”,原生Transformer架构完全有能力在时间序列预测任务上取得顶尖性能。iTransformer不仅在性能上树立了新的标杆,还解决了现有Transformer方法的一系列核心痛点,为未来构建可扩展、可泛化的时间序列基础模型提供了一个极具前景的新方向。