KAN: Kolmogorov-Arnold Networks

TL;DR

本文提出了一种名为科尔莫戈罗夫-阿诺德网络（Kolmogorov-Arnold Networks, KANs）的新型神经网络架构，其将可学习的激活函数置于网络边缘（“权重”）而非节点上，从而在函数拟合等任务中，相比于传统的多层感知机（MLPs），展现出更高的精度和可解释性。

关键定义

相关工作

当前，多层感知机（MLPs）是深度学习中用于逼近非线性函数的默认模型，其能力由通用逼近定理（Universal Approximation Theorem）保证。然而，MLPs也存在显著缺陷，例如在Transformer模型中，MLPs占据了大量参数且可解释性较差。此外，虽然MLPs能够学习高维函数，但它们在逼近简单的一维函数时效率不高。另一方面，样条（splines）拟合在一维情况下非常精确，但遭遇严重的维度灾难（Curse of Dimensionality, COD）。

本文旨在解决MLPs在精度和可解释性上的瓶颈，同时避免样条拟合的维度灾难问题。具体而言，本文的目标是设计一种新的网络架构，能够结合MLPs学习组合结构的能力和样条精确拟合一维函数的能力，从而在保证精度的前提下，获得更好的可解释性和更优的缩放性质（scaling laws）。

本文方法

KAN架构的灵感与设计

本文的架构设计灵感来源于科尔莫戈罗夫-阿诺德表示定理。该定理指出，任何多元连续函数 $f(x_1, \dots, x_n)$ 都可以表示为一维连续函数和加法的有限组合：

\[f(\mathbf{x})=f(x_{1},\cdots,x_{n})=\sum_{q=1}^{2n+1}\Phi_{q}\left(\sum_{p=1}^{n}\phi_{q,p}(x_{p})\right)\]

这个定理表明，高维函数的学习本质上可以分解为学习一组一维函数。

基于此，本文提出了KAN架构。与将固定的非线性激活函数放在节点上的MLP不同，KAN将可学习的激活函数放在了网络的边上。 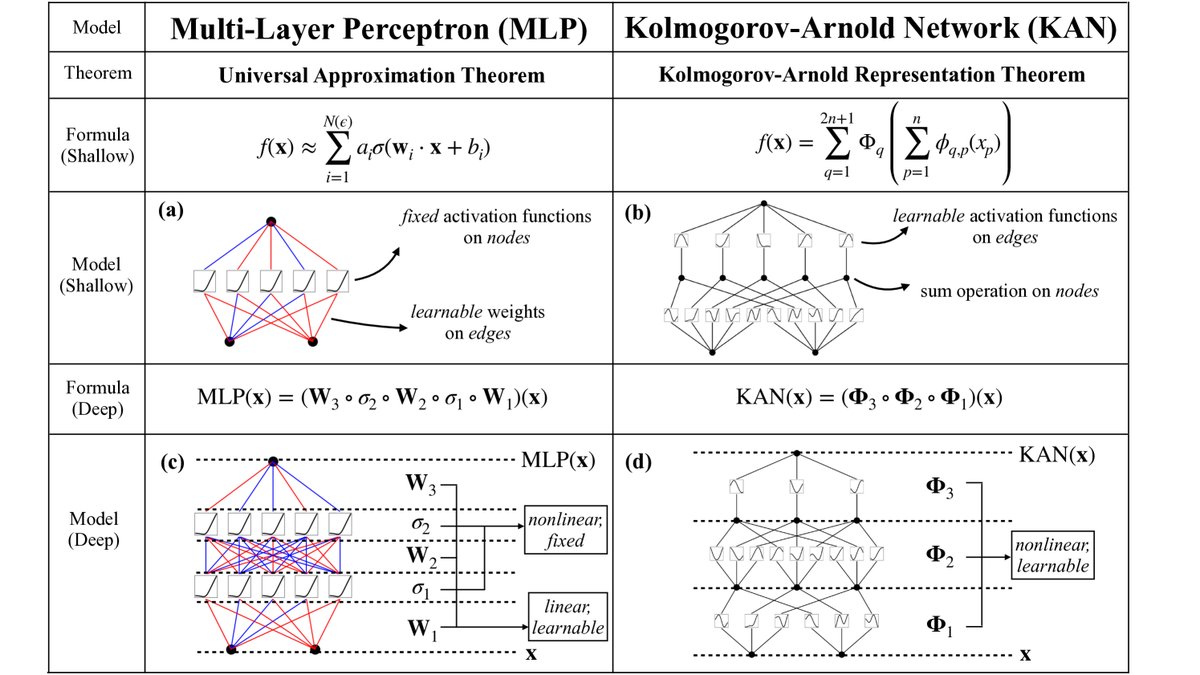MLPs vs. KANs 图1：多层感知机（MLPs）与科尔莫戈罗夫-阿诺德网络（KANs）的对比。

一个KAN网络由多个KAN层堆叠而成。一个从 $n_{\rm in}$ 维输入到 $n_{\rm out}$ 维输出的KAN层，是一个由 $n_{\rm in} \times n_{\rm out}$ 个一维激活函数 $\phi_{q,p}$ 组成的矩阵。对于第 $l$ 层的第 $i$ 个节点，其输出 $x_{l,i}$ 作为输入，传递给连接第 $l$ 层和第 $l+1$ 层的边上的激活函数 $\phi_{l,j,i}$。第 $l+1$ 层的第 $j$ 个节点的输入值是所有传入信号经过激活函数后的总和：

\[x_{l+1,j}=\sum_{i=1}^{n_{l}}\phi_{l,j,i}(x_{l,i})\]

一个完整的KAN网络是多层这种操作的组合：

\[{\rm KAN}(\mathbf{x})=(\mathbf{\Phi}_{L-1}\circ\mathbf{\Phi}_{L-2}\circ\cdots\circ\mathbf{\Phi}_{0})\mathbf{x}\]

KAN的符号表示与样条参数化 图2：左图为网络中激活流的符号表示。右图展示了一个激活函数如何被参数化为B样条，允许在粗细网格间切换。

创新点

KAN最本质的创新在于将学习的重心从线性权重转移到了自适应的激活函数上。MLP的结构是固定的线性变换（权重矩阵）与固定的非线性激活函数交织，而KAN将这两者统一为边上的可学习函数。

优点

这个设计的核心优点是它巧妙地结合了MLPs和样条的优势：

  1. 克服维度灾难：像MLPs一样，KANs通过堆叠层来学习数据的组合结构（外部自由度），从而避免了传统样条拟合的维度灾难。
  2. 高精度拟合：像样条一样，KANs的每个激活函数可以非常精确地学习一维函数（内部自由度），这使得它们在拟合具有内在低维结构的高维函数时比MLPs更高效、更精确。

实现细节与理论保证

论文组织结构图 图3：论文组织结构图，展示了KANs的数学基础、精度和可解释性。

提升KANs精度与可解释性的技术

精度：网格扩展

为了进一步提升精度，本文提出了网格扩展技术。模型可以从一个具有少量网格点（参数较少）的粗糙样条开始训练。当训练进入平台期时，可以通过在现有样条函数上拟合一个新的、具有更密集网格点的样条，来增加模型容量，而无需重新从头训练。这个过程可以重复进行，使得损失呈现阶梯式下降。 网格扩展效果 图4：通过网格扩展可以提升KANs的精度。损失曲线呈现阶梯式下降，且测试RMSE随网格大小G呈现幂律缩放。

可解释性：简化与交互

为了让KANs更具可解释性，本文提出了一套简化流程，使用户可以与模型交互，从而发现数据背后隐藏的符号公式。

  1. 稀疏化：通过L1范数和熵正则化，鼓励网络中的大部分激活函数变为零，从而使网络结构稀疏化。
  2. 可视化：将学习到的激活函数绘制出来，其幅度大小通过透明度表示，不重要的连接会淡出。
  3. 剪枝：根据激活函数的输入和输出得分，自动剪除不重要的节点，从而得到一个更小的、与问题结构更匹配的KAN架构。
  4. 符号化：当用户通过可视化发现某个激活函数形似已知的数学函数（如 \(sin\), \(x^2\)）时，可以手动或通过系统建议将其固定为该符号形式。系统会自动拟合仿射变换参数以匹配尺度和平移。

下图展示了一个用户如何通过这个流程，从一个[2,5,1]的KAN逐步简化，最终发现目标函数 $f(x,y)=\exp(\sin(\pi x)+y^2)$ 的符号表达式。 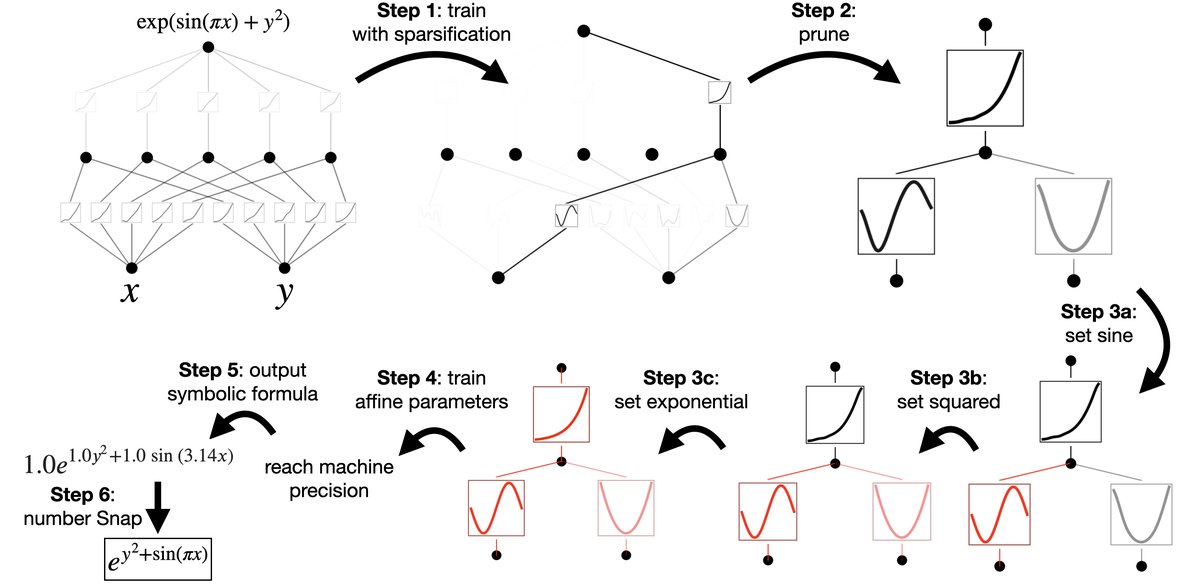符号回归示例 图5：一个与KAN交互进行符号回归的示例。

实验结论

虽然完整的实验细节在论文后续章节，但根据已提供的内容和引用可以总结出以下结论：