KTO: Model Alignment as Prospect Theoretic Optimization

• ArXiv URL: http://arxiv.org/abs/2402.01306v4

• 作者: Kawin Ethayarajh; Douwe Kiela; Winnie Xu; Dan Jurafsky; Niklas Muennighoff

• 发布机构: Contextual AI; Stanford University

---

TL;DR

本文提出了一种名为KTO (Kahneman-Tversky Optimization) 的新型大模型对齐方法，它基于前景理论，仅需“可取”或“不可取”的二元反馈信号，便能在10亿到300亿参数规模的模型上达到甚至超越基于偏好数据的DPO方法的性能。

关键定义

本文提出了几个核心概念，用于从认知科学（前景理论）的视角重新审视和构建模型对齐方法：

1. 前景理论 (Prospect Theory): 一个描述人类在不确定情况下如何进行决策的认知科学理论。其核心观点是，人类对价值的感知是相对的（基于一个参考点），并且对损失比对等量收益更敏感（损失厌恶）。
2. 人类感知损失函数 (Human-Aware Losses, HALOs): 本文提出的一个损失函数家族。它们将模型对齐问题建模为最大化人类的主观价值。这类损失函数的特点是，它们包含一个价值函数 $v$，该函数作用于“模型隐含奖励”与一个“参考点”之间的差值，从而模拟了人类的认知偏差（如损失厌恶和风险规避）。
3. 隐含奖励 (Implied Reward): 定义为 $r_{\theta}(x,y) = \beta \log[\pi_{\theta}(y \mid x)/\pi_{\text{ref}}(y \mid x)]$。它衡量了从参考模型 $\pi_{\text{ref}}$ 变为当前模型 $\pi_{\theta}$ 时，生成特定输出 $y$ 的对数概率增益，可以理解为模型认为该输出有多“好”。
4. KTO (Kahneman-Tversky Optimization): 本文提出的核心对齐方法。它是一种HALO，其损失函数直接源自Kahneman和Tversky的价值函数模型。与DPO最大化偏好数据的对数似然不同，KTO旨在直接最大化生成结果的（前景理论）效用，且只需要关于单个输出是“可取”还是“不可取”的二元反馈。

相关工作

目前，大型语言模型（LLM）的对齐（Alignment）主流方法是基于人类反馈的强化学习（RLHF）。RLHF通常分为两步：首先，训练一个奖励模型来拟合人类的偏好数据（例如，输出$y_w$优于$y_l$）；然后，使用PPO等强化学习算法来优化语言模型，使其在最大化奖励的同时，不过分偏离原始的SFT模型（通过KL散度惩罚）。

然而，RLHF流程复杂、训练不稳定。直接偏好优化（Direct Preference Optimization, DPO）作为一种更简单、稳定的替代方案应运而生。DPO通过一个巧妙的推导，将RLHF的目标转化为一个简单的、可以直接在偏好数据上优化的分类损失函数，避免了显式的奖励建模和复杂的RL训练。

本文旨在解决的关键问题是：当前最有效的对齐方法（如RLHF和DPO）都严重依赖于成对的偏好数据（$(x, y_w, y_l)$），而这类数据在现实世界中收集成本高、速度慢、数量稀缺。本文试图探究是否必须使用偏好数据，并希望开发一种仅依赖更易获取的二元反馈信号（即判断单个输出是“好”还是“坏”）就能实现高效对齐的方法。

本文方法

前景理论视角与HALOs

本文首先从认知科学的前景理论出发，为现有对齐方法的成功提供了新的解释。前景理论指出，人类对价值的感知并非线性的，而是具有参考点依赖、损失厌恶和风险态度等特征。

作者发现，像DPO和PPO-Clip这类成功的对齐方法，其损失函数在数学形式上隐式地体现了这些人类认知偏差。例如，它们都包含一个非线性的价值函数，并且对负向奖励（损失）的惩罚斜率与正向奖励（收益）不同。

图1：不同人类感知损失（HALOs）所隐含的人类从随机变量结果中获得的效用函数。注意，这些隐含的价值函数与前景理论中的典型人类价值函数共享诸如“损失厌恶”等特性。

基于此洞察，本文正式定义了人类感知损失函数 (HALOs) 这一概念。一个损失函数如果可以被表示为对某个价值函数 $v$ 的期望，其中 $v$ 作用于“隐含奖励”与一个“参考点”的差值上，那么它就是HALO。

\[f(\pi\_{\theta},\pi\_{\text{ref}}) = \mathbb{E}\_{x,y\sim\mathcal{D}}[a\_{x,y}v(r\_{\theta}(x,y)-\mathbb{E}\_{Q}[r\_{\theta}(x,y^{\prime})])]+C\_{\mathcal{D}}\]

作者证明了DPO和PPO-Clip都属于HALOs。实验也初步表明，属于HALO的方法（DPO、一种离线PPO变体）在性能上普遍优于非HALO方法（如CSFT、SLiC），尤其是在大模型上，这说明损失函数本身的设计（其蕴含的归纳偏置）对对齐效果至关重要。

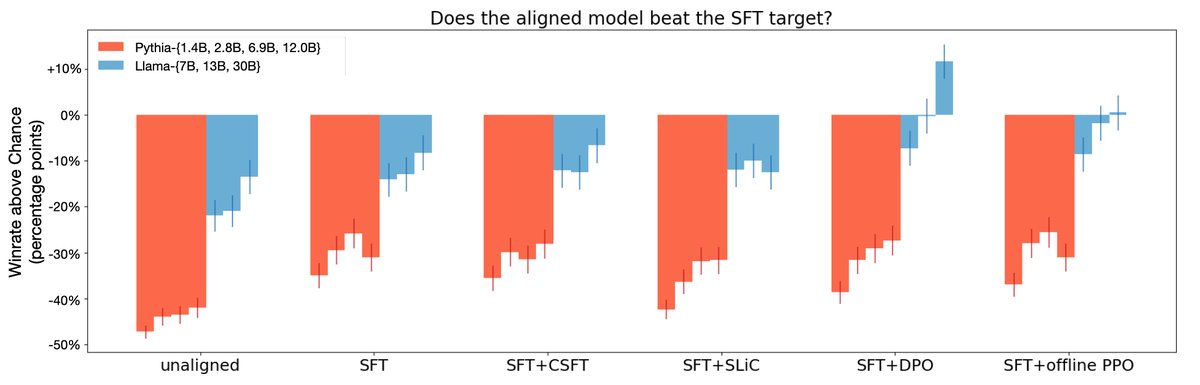图2：HALOs（DPO，离线PPO变体）在GPT-4评测中胜率优于非HALOs（SLiC，CSFT）。

KTO：方法推导与创新

创新点

传统方法如DPO通过最大化偏好对的对数似然来间接优化模型，而KTO的本质创新在于直接最大化生成内容的预期效用（utility）。这个效用函数直接借鉴了前景理论中对人类价值感知的建模。

方法细节

作者基于Kahneman-Tversky的经典价值函数形式，设计了KTO损失函数。为了优化稳定性和可控性，做了一些修改：

1. 用形状类似但更平滑的logistic函数 $\sigma$ 替代了原版中的幂函数。
2. 引入超参数 $\beta$ 控制风险厌恶程度，$\beta$ 越大，价值函数曲线越弯曲，表示对收益的风险厌恶和对损失的风险寻求倾向越强。
3. 引入 $\lambda_D$ 和 $\lambda_U$ 分别控制对“可取”（desirable）和“不可取”（undesirable）样本的权重，以实现类似“损失厌恶”的效果或处理数据不平衡。

最终的KTO损失函数定义为：

\[L\_{\text{KTO}}(\pi\_{\theta},\pi\_{\text{ref}})=\mathbb{E}\_{x,y\sim D}[\lambda\_{y}-v(x,y)]\]

其中，价值函数 $v(x, y)$ 根据样本是可取还是不可取，形式不同：

\[\begin{split} r\_{\theta}(x,y)&=\log\frac{\pi\_{\theta}(y \mid x)}{\pi\_{\text{ref}}(y \mid x)} \\ z\_{0}&=\text{KL}(\pi\_{\theta}(y^{\prime} \mid x)\ \mid \pi\_{\text{ref}}(y^{\prime} \mid x)) \\ v(x,y)&=\begin{cases}\lambda\_{D}\sigma(\beta(r\_{\theta}(x,y)-z\_{0})) & \text{if }y\sim y\_{\text{desirable}} \mid x\\ \lambda\_{U}\sigma(\beta(z\_{0}-r\_{\theta}(x,y))) & \text{if }y\sim y\_{\text{undesirable}} \mid x\\ \end{cases} \end{split}\]

• 参考点 $z_0$: 在KTO中，参考点被设定为当前策略 $\pi_\theta$ 相对于参考策略 $\pi_{\text{ref}}$ 的KL散度。这在直觉上代表了当前模型为生成一个“平均”输出所需付出的“努力”。在实际操作中，为了计算效率，使用同批次（microbatch）中其他样本的输出来进行有偏但高效的估计 $\hat{z}_0$。
• 工作机制: KTO通过这个设计，激励模型去学习可取输出的内在特征。如果模型只是粗暴地提高某个可取样本 $y$ 的概率，这会导致整体KL散度 $z_0$ 上升，从而抵消 $r_\theta(x,y)$ 的增长，使得损失无法有效下降。只有当模型学会了区分“好”与“坏”的根本模式，才能在提高好样本概率的同时，不显著增加（甚至降低）KL散度，从而真正优化损失函数。

数据与超参数

• 数据处理：KTO可以直接使用天然的二元标签数据。对于现有的偏好数据集（$y_w \succ y_l$），可以简单地将 $y_w$ 视为“可取”样本，将 $y_l$ 视为“不可取”样本。
• 超参数建议：本文给出了实用的超参数设置建议。例如，KTO的最佳学习率通常比DPO高（如5e-6 vs 5e-7）。$\beta$ 值和 $\lambda$ 值的选择与模型大小、是否进行SFT以及数据中好/坏样本的比例有关。

| 模型 | 方法 | 学习率 | $\beta$ | AlpacaEval (LC) $\uparrow$ | BBH $\uparrow$ | GSM8K (8-shot) $\uparrow$ | | — | — | — | — | — | — | — | | Llama-3 8B | SFT+KTO | 5e-6 | 0.05 | 10.59 | 65.15 | 60.20 | | Llama-3 8B | KTO | 5e-6 | 0.10 | 11.25 | 65.26 | 57.92 | | Qwen2.5 3B Instruct | SFT+KTO | 5e-6 | 0.10 | 13.01 | 32.39 | 61.11 | | Qwen2.5 3B Instruct | KTO | 5e-6 | 0.50 | 16.63 | 20.41 | 60.35 | 表1: 在UltraFeedback上对齐不同模型的推荐超参数设置。

实验结论

本文通过一系列实验，验证了KTO的有效性。

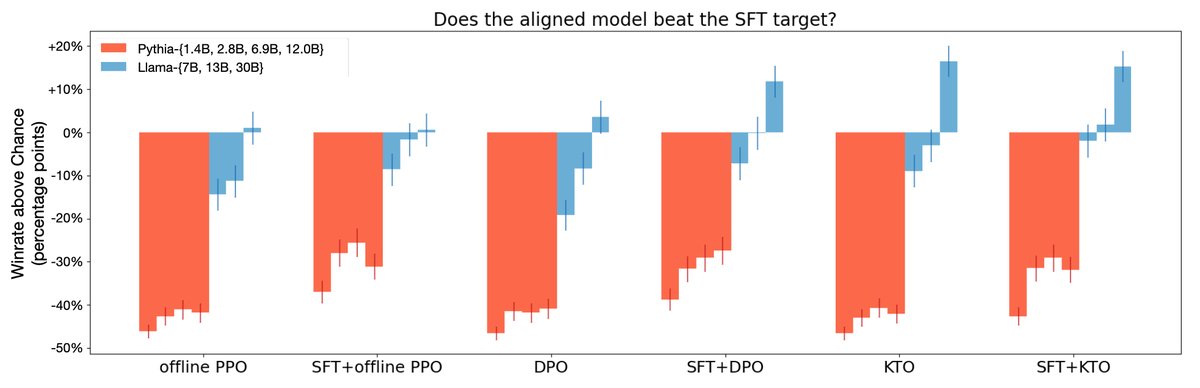图3: GPT-4评测的胜率表明，KTO在所有模型规模上表现与DPO相当或更优。对于Llama系列模型，单独使用KTO的效果甚至能媲美SFT+DPO。

1. 性能优越: 在10亿到300亿参数规模的Pythia和Llama系列模型上，将偏好数据拆分为二元数据后，SFT+KTO的性能与SFT+DPO相当甚至更优。在GSM8K等特定任务上，KTO带来的提升尤为显著（见下表）。

| | | | | | | — | — | — | — | — | | 数据集 ($\rightarrow$) | MMLU | GSM8k | HumanEval | BBH | | 指标 ($\rightarrow$) | EM | EM | pass@1 | EM | | SFT | 57.2 | 39.0 | 30.1 | 46.3 | | DPO | 58.2 | 40.0 | 30.1 | 44.1 | | ORPO ($\lambda=0.1$) | 57.1 | 36.5 | 29.5 | 47.5 | | KTO ($\beta=0.1$, $\lambda_{D}=1$) | 58.6 | 53.5 | 30.9 | 52.6 | | KTO (one-$y$-per-$x$) | 58.0 | 50.0 | 30.7 | 49.9 | | KTO (no $z_0$) | 58.5 | 49.5 | 30.7 | 49.0 | 表2（部分）: Zephyr-β-SFT在UltraFeedback上对齐一轮的基准测试结果，KTO在GSM8k和BBH上优势明显。

1. 可跳过SFT: 对于足够大的模型（如Llama-13B/30B），直接在预训练模型上进行KTO对齐，其性能可以媲美先进行SFT再进行KTO的版本。而DPO如果跳过SFT，则会出现生成内容冗长、胡言乱语等问题。

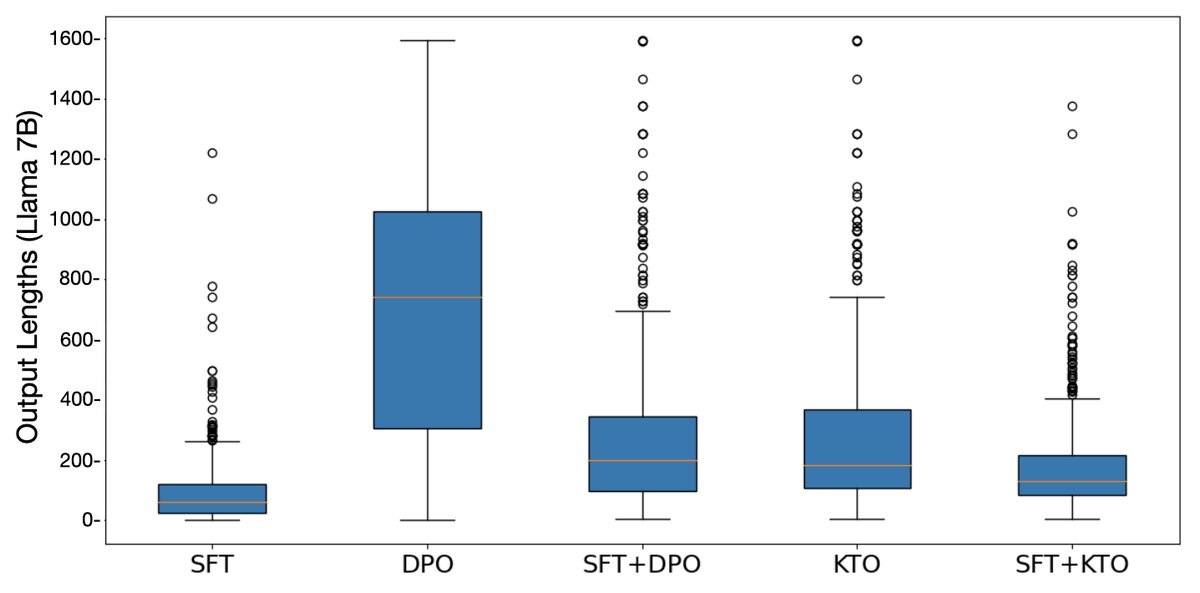图4: 未经SFT直接对齐时，DPO模型倾向于生成过长的回答，而KTO则没有这个问题。

1. 数据鲁棒性: 实验证明KTO的优异表现并非“窃取”了偏好数据的配对信息。
   • 即使在数据极度不平衡（例如，丢弃90%的可取样本，使好/坏样本比例为1:10）的情况下，KTO通过调整$\lambda$权重，依然能超过DPO的性能。
   • 在使用非配对的、每个输入只有一个输出的数据集上，KTO（one-$y$-per-$x$）即便数据量减半，性能依旧优于在完整配对数据上训练的DPO。

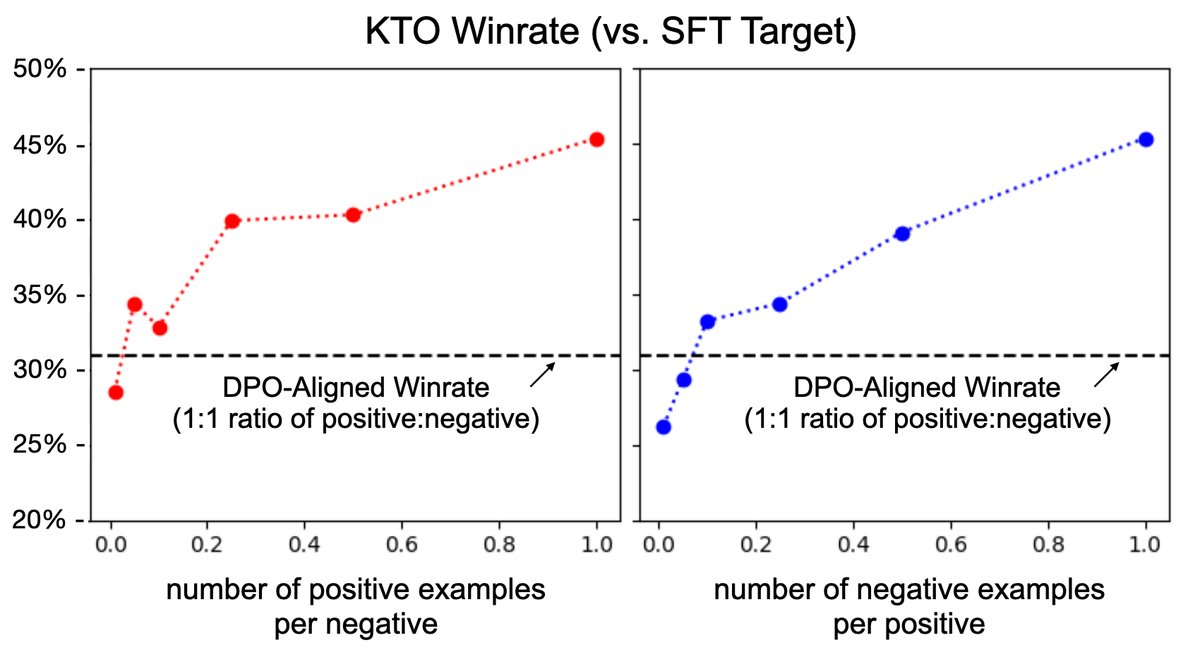图5: 即使可取样本极少（例如，好坏样本比例为1:10），KTO对齐的Llama-7B模型性能仍能匹敌或超过DPO。

1. 设计合理性: 对KTO损失函数的消融实验表明，其关键设计（如参考点 $z_0$、对称的价值函数曲线）对于最终性能至关重要。移除这些组件会导致性能显著下降。

最终结论是：KTO是一种非常有效且数据高效的大模型对齐方法。它的成功表明，从人类认知科学（前景理论）中汲取灵感来设计损失函数是一个富有成效的方向。更广泛地说，不存在一个万能的、在所有场景下都最优的对齐损失函数；最佳选择取决于特定任务所需的归纳偏置，这是一个在模型对齐中应被深思熟虑的因素。