Language Self-Play For Data-Free Training

TL;DR

本文提出了一种名为语言自博弈（Language Self-Play, LSP）的无数据训练方法，通过构建一个强化学习框架，让大型语言模型在“挑战者”（生成难题）和“解答者”（解答问题）两种角色间自我对抗，从而在无需外部训练数据的情况下实现持续自我提升。

关键定义

本文提出或沿用了以下关键概念：

相关工作

当前，大型语言模型（LLMs）的进步，尤其是在对齐和能力增强方面，高度依赖强化学习（RL）技术。然而，包括RL在内的所有主流机器学习范式都面临一个共同的瓶颈：对大规模、高质量训练数据的依赖。无论是监督学习还是强化学习，都需要大量的任务示例（在LLM中表现为提示/prompts），而这些数据的数量和质量限制了模型能力的持续提升。

为解决此问题，研究界探索了合成数据训练、元学习数据增强等方法。本文则另辟蹊径，旨在从根本上解决LLM训练的“数据依赖”问题，探索一种让模型在完全没有外部数据供给的情况下实现自我完善的路径。

本文方法

本文提出了一种名为语言自博弈（LSP）的算法，其核心思想是将LLM的持续学习过程建模为一个双人竞争游戏，并通过自博弈（self-play）的方式，让单个模型驱动这个过程，从而实现无数据训练。

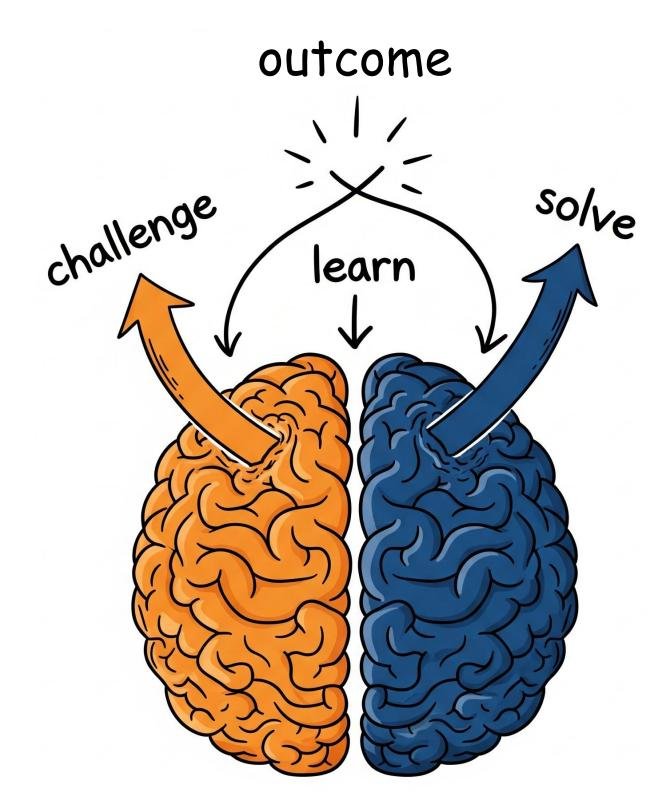
Figure 1: 语言自博弈智能体在两种模式下运行：挑战者和解答者。挑战者生成指令，解答者遵循指令。解答者学习改进对提示的响应，而挑战者则学习使提示变得更困难。两种模式由同一个模型实例化，从而能够在不断提高质量的自生成数据上进行永久训练。

创新点

1. 将训练过程构建为自博弈游戏

LSP框架将LLM的能力提升抽象为一个“挑战者”（Challenger）和“解答者”（Solver）之间的极小极大博弈（minimax game）：

\[\min_{\pi_{\rm Ch}} \max_{\pi_{\rm Sol}} \mathbb{E}_{\mathbf{q} \sim \pi_{\rm Ch}, \mathbf{a} \sim \pi_{\rm Sol}} [R(\mathbf{q}, \mathbf{a})]\]

其中，“解答者”($\pi_{Sol}$) 努力最大化任务奖励 $R(\mathbf{q}, \mathbf{a})$，而“挑战者”($\pi_{Ch}$) 则试图生成使“解答者”得分最小化的查询 $q$。

2. 单一模型实现自博弈

与需要额外对抗模型的传统对抗训练不同，LSP利用自博弈的思想，让单个语言模型 $\pi^{\theta}$ 通过不同的提示（prompting）来扮演两个角色：

这种设计不仅节省了计算资源，还利用了自博弈在对称游戏中已被证明的有效性和稳定性。

Box 1: 挑战者提示

背景

语言任务以（输入，输出）元组的形式出现。给定一个输入，语言智能体产生一个输出以响应输入提出的请求。例如，在问答任务中，输入是问题，输出是问题的答案。在文章标题生成中，输入是文章，输出是捕捉该文章精髓的标题。

请求

为语言任务’{task}’生成一个将传递给另一个语言智能体的输入。也就是说，你对此提示的响应必须是该语言任务的有效输入。输入可以是简单的、中等的、困难的，或者仅仅是带有噪声的。它应该对应智能体进行压力测试，或推动其进行创造性思考。请注意，在本次运行中，你将只生成一个示例。

细节

在下面的[Start Generation]和[End Generation]标签之间，你会找到一个你必须遵循的模板——你将复制模板的文本（不含标签）并用你自己生成的内容填充模板中用花括号{}标记的占位符。例如，如果占位符是{冰淇淋口味}，你应该生成一个冰淇淋口味的名称。 [Start Generation] ‘{template}’ [End Generation]

最后备注

不要在你生成的输入中包含回答（输出）、提示或泄露信息。输入不能要求语言智能体无法执行的动作。一旦你的响应满足模板，立即停止生成。你的响应不能包含[Start Generation]和[End Generation]标签。严格遵循模板，除非任务和模板都为None或为空（此时你应该根据自己的最佳判断生成输入）。现在，作为对此提示的响应，请遵循模板为语言任务’{task}’生成一个输入。

Box 2: 挑战者生成的提示示例

500次迭代后： 在学生主导的项目式学习方面，蒙台梭利教室和传统教室设置在方法上有什么典型区别？

1000次迭代后： 按照以下步骤，建造一艘功能性潜艇，该潜艇仅使用一个装有12升空气的水肺气瓶，能够潜至水下100米深。潜艇必须能够在该深度承受水压而不坍塌，并应在20分钟后自动浮出水面。

1500次迭代后： 遵循指示，创建一个结合了Python和Haskell的新编程语言，该语言具有独特的语法和语义，并且仅使用标准库，无任何外部依赖，能够在64位x86处理器上编译和运行，代码长度不超过1000个字符。

3. 基于相对优势的强化学习更新

为了有效进行RL训练，本文借鉴了GRPO算法中的“组内相对”（group-relative）技巧来计算优势函数：

  1. 解答者优势 $A_{Sol}$: 对于一个查询 $q_i$，“解答者”生成 $G$ 个回答。所有回答的平均奖励 $V(\mathbf{q}_i) = \frac{1}{G} \sum_{j=1}^G R(\mathbf{q}_i, \mathbf{a}_i^j)$ 被用作基线（baseline）。每个回答的优势为 $A_{Sol}(q_i, a_i^j) = R(q_i, a_i^j) - V(q_i)$。这激励“解答者”生成比自己平均水平更好的回答。
  2. 挑战者优势 $A_{Ch}$: “挑战者”的奖励被定义为 $-V(q_i)$，即“解答者”在该问题上的平均表现越差，“挑战者”获得的奖励越高。其优势函数为 $A_{\mathsf{Ch}}(\mathbf{q}_i) = V - V(\mathbf{q}_i)$，其中 $V$ 是所有查询的平均基线。这激励“挑战者”去探索能让“解答者”表现不佳的“难题”。

4. 引入质量自奖励以稳定训练 (LSP vs LSP-Zero)

单纯的零和博弈（LSP-Zero）可能导致模型在训练后期生成无意义的对抗性内容。为了解决这个问题，本文引入了质量自奖励 ($R_Q$)，一个由参考模型自身生成的、用于评估交互质量的分数（见 Box 3）。该奖励被同时加到“解答者”和“挑战者”的奖励中，将游戏转变为非零和博弈。这引导自博弈过程朝着更有意义、更高质量的方向发展，从而实现了更稳定和长期的训练。

Box 3: 自奖励提示

审查用户-助手交互（用户的指令和相应的响应），并使用下面描述的加法式7分整数评分系统对其进行评分。基础分为0分。根据每个二元标准的满足情况累积分数（如果满足标准+1，否则+0）： 1. +1 当且仅当用户的任务可以从指令中清晰地识别。 2. +1 当且仅当指令清晰、具体且结构良好。 3. +1 当且仅当该用户能够清楚地理解响应。 4. +1 当且仅当响应解决了用户问题的很大部分，但不一定完全完整。 5. +1 当且仅当响应有用且全面地回答了问题的核心要素。 6. +1 当且仅当响应文笔清晰、简洁、组织良好且有帮助。 7. +1 当且仅当该用户很可能会喜欢响应的形式和风格。 {instruction} {response} 在检查了用户的指令和响应之后： - 简要说明你的评分理由，总字数不超过100字。记住每个标准的分数。 - 在和标签之间写下所有单项得分的加法计算（例如：1+0+1+0+1+1+0=4）。结果即为总分。确保计算正确！ - 最后在和标签之间给出总分值，范围从0到7（例如：4）。正确的格式至关重要！

算法流程

完整的LSP算法流程如下所示，它集成了查询生成、回答生成、奖励计算和模型参数更新。

Algorithm 1 语言自博弈 (Language Self-Play)

需要: 预训练模型 $\pi^{\theta}$，奖励函数R(q, a)，挑战者系数 $\alpha_{Ch}$

实验结论

本文在 AlpacaEval 基准上使用 Llama-3.2-3B-Instruct 作为基础模型进行了实验，以验证LSP方法的有效性。

1. 从基础模型开始训练

该实验比较了无数据训练的 LSP 和 LSP-Zero 与在 Alpaca 数据集上使用传统RL方法（GRPO）进行有数据训练的模型。

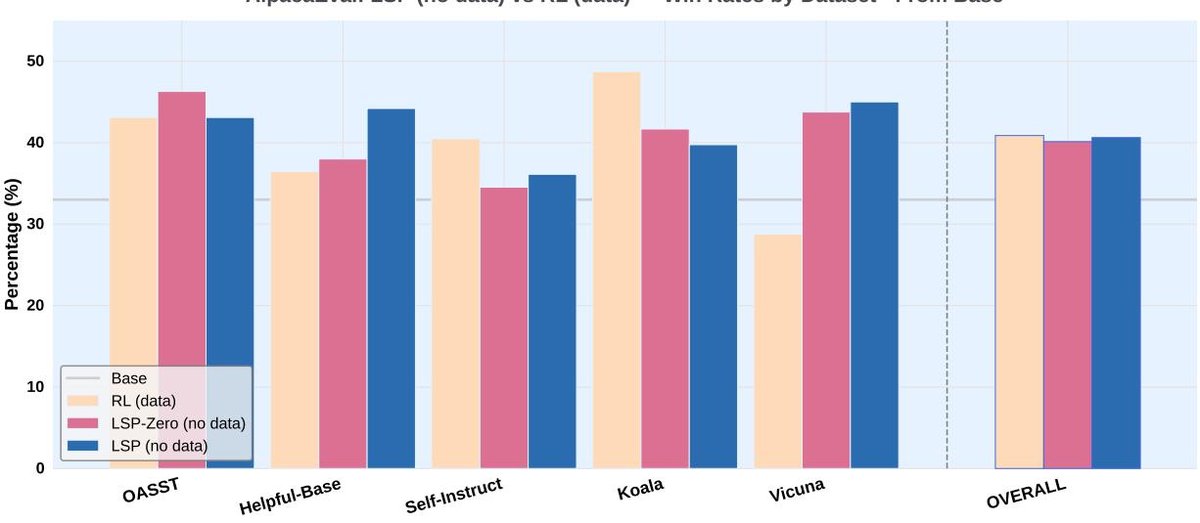
Figure 2: 在AlpacaEval基准上，使用RL（GRPO，有数据支持，黄色条）和LSP-Zero & LSP（无数据，分别为红色和蓝色条）训练的模型与基础模型（Llama-3.2-3B-Instruct）的胜率对比。所有算法都在整体基准上优于基础模型。GRPO, LSP-Zero和LSP的总体胜率分别为 40.9%, 40.1%和40.6%。

2. 作为已有模型的后续训练阶段

该实验将 LSP 应用于一个已经通过有数据RL（GRPO）训练过的模型，探索其作为进一步微调手段的潜力。

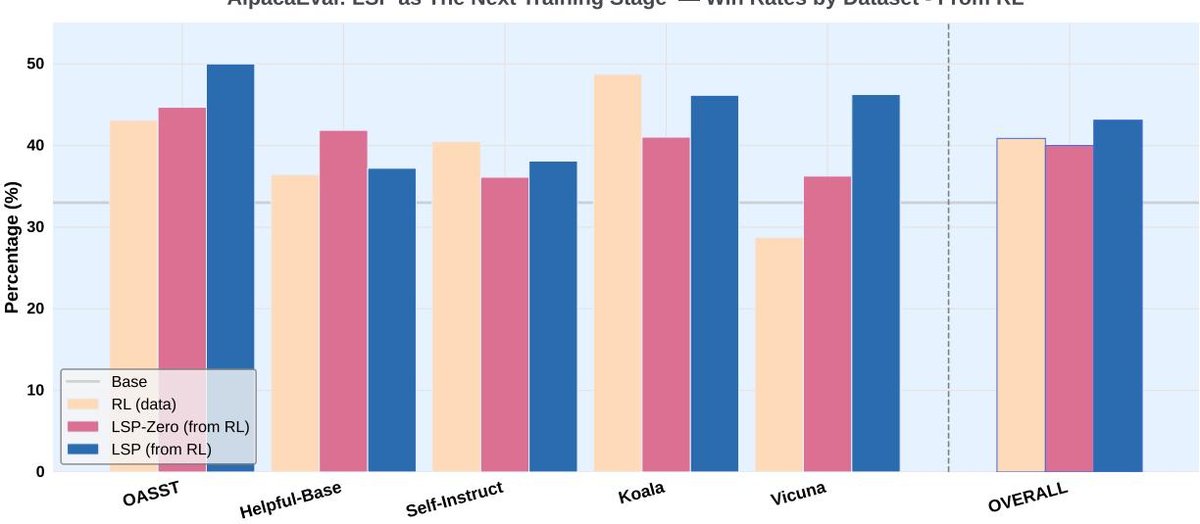
Figure 3: 在AlpacaEval基准上，使用LSP-Zero和LSP（无数据，红色和蓝色条）训练的模型与其初始模型——用GRPO（有数据支持，黄色条）训练的模型——的胜率对比。LSP在整体上和在Vicuna数据集上的表现均优于GRPO。具体胜率分别为GRPO 40.9%，LSP-Zero 40.0%，LSP 43.1%。

结论与局限