Large Language Model Sourcing: A Survey

ArXiv URL: http://arxiv.org/abs/2510.10161v1
作者: Xueqi Cheng; Huawei Shen; Sunhao Dai; Jia Gu; Zihao Wei; Zhiyi Yin; Xiang Li; Zenghao Duan; Liang Pang; Kangxi Wu; 等11人
发布机构: Chinese Academy of Sciences; Renmin University of China; University of Chinese Academy of Sciences

大语言模型溯源：一篇综述

引言

ChatGPT的发布标志着大语言模型（Large language models, LLMs）发展的一个分水岭，推动了自然语言处理进入一个变革性的新时代。诸如DeepSeek、Qwen、GPT-4、Claude、LLaMA3和Gemini等模型是这一爆炸性增长的例证。它们共同标志着人工智能的范式转变——从支持分类和预测等客观任务，转向赋能更主观、面向决策的推理。这些模型如今在编程、教育、医疗和法律服务等多个领域展现出惊人的通用性。

然而，LLMs的广泛应用也放大了其固有的风险。模型训练和检索数据中固有的偏见可能加剧社会不公。幻觉和事实错误是另一个严重问题，尤其是在医学和法律等敏感领域。LLMs的不透明性使得问责变得复杂，而像提示注入和训练数据投毒等安全漏洞则为恶意利用创造了机会。

在这些挑战中，两个问题尤为基础：生成内容的不可区分性和模型自身结构的“黑箱”特性。这凸显了对强大的输出溯源机制的迫切需求。溯源通过在LLM生命周期中建立可验证的责任链，系统性地降低风险，从而在关键应用中培养用户信任。它可以将有害输出精确归因于特定模型或架构组件，或将侵权内容追溯到原始训练样本或外部来源。

为实现这一目标，本文提出了一个统一的溯源框架，该框架整合了模型和数据两个视角，并系统地将现有方法分为先验 (prior-based) 和后验 (posterior-based) 两大范式。先验方法在模型训练或数据准备期间主动嵌入可追踪标记，而后验方法则在生成后通过分析模型输出来追溯推断来源。

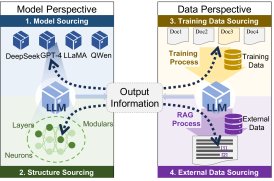
本文的溯源框架涵盖了四个相互关联的维度，为评估现代LLM生态系统中的来源、责任和可追溯性提供了全面的视角。

模型溯源 (Model Sourcing)：专注于将生成内容归因于特定的LLM或人类作者。这对于遏制由合成内容引发的错误信息至关重要。
结构溯源 (Structure Sourcing)：研究架构组件（如参数配置、注意力机制）如何影响模型行为，从而揭示其不透明的决策过程。
训练数据溯源 (Training Data Sourcing)：将生成输出的因果关系归因于特定的训练样本，以解决与偏见、敏感或噪声数据相关的风险。
外部数据溯源 (External Data Sourcing)：将输出内容归因于用户输入或检索到的外部知识，有助于检测对抗性提示、操纵或上下文模糊性。

大语言模型溯源的四个维度。从模型角度，输出信息可归因于特定模型本身（模型溯源）或其内部架构和机制（结构溯源）。从数据角度，输出信息可追溯到模型的训练样本（训练数据溯源）或与用于对齐或参考的特定外部语料库相关联（外部数据溯源）。

本文的核心创新在于：

覆盖LLM内容生命周期的整体范围：将模型、模型结构、训练数据和外部数据四个相互关联的溯源维度整合到一个统一的溯源范式中。
归因方法的双范式分类体系：为每个维度，将方法系统化为先验（主动嵌入可追溯性）和后验（回顾性推断）方法，揭示了设计时可验证性与事后可分析性之间的关键权衡。

大语言模型溯源方法的分类体系。

LLM溯源的理论框架

本章重点围绕LLM溯源的核心主题，系统介绍相关的研究问题与动机、关键概念的统一定义、研究领域的范围以及溯源方法的分类标准。

研究背景与动机

LLMs在快速发展的同时也面临一系列亟待解决的关键挑战。

从模型角度看，风险主要源于内容不可区分性和结构不透明性。一方面，LLM生成内容与人类创作内容之间的界限日益模糊。这种拟人化特征不仅可能嵌入不合规或有害信息，还具有很强的隐蔽性。另一方面，现代LLM固有的结构复杂性和“黑箱”性质是关键的技术风险因素。其决策过程难以被人类解释，透明度低，这使得识别和纠正内部偏见、预测和控制模型行为变得异常困难。

从数据角度看，风险主要源于对训练数据的内在依赖和外部数据的脆弱性。训练数据的质量直接决定了模型的行为和性能，数据集中的偏见、噪声或不完整性会传递到实际应用中。此外，训练语料中可能包含的敏感个人信息有被模型“记忆”并在生成中无意泄露的风险。同时，用户交互的动态性带来了输入漏洞，恶意行为者可能通过构造对抗性提示来操纵模型。

鉴于这些挑战，对溯源技术的研究变得日益重要。LLM溯源旨在将模型行为与其内部机制和外部依赖联系起来，为解决当前问题提供关键见解。例如：

对模型及其生成内容进行溯源，可以追踪LLM的创建者、训练过程和使用历史，对于确保数据安全、防止恶意攻击和识别版权侵犯至关重要。
溯源能够识别训练数据的来源和质量，有助于定位偏见和数据噪声的潜在来源，从而进行针对性改进。
对模型结构的溯源可以揭示架构设计和参数配置，结合训练数据可追溯性，有助于理解模型的知识表示和推理模式，从而解决“黑箱”问题，增强用户信任。

溯源方法的统一-定义与分类

在LLM溯源领域，方法论可根据其时间点和机制基础，分为两大范式：后验溯源 (Posterior-based Sourcing) 和 先验溯源 (Prior-based Sourcing)。

后验溯源强调在模型已训练完毕、输出已生成的情况下进行。它基于输出和上下文，对候选来源进行统计一致性检验和敏感性评估，从而推断出最可能的模型来源和主要影响因素。 先验溯源则强调在生成之前，通过在训练数据或模型本身中植入稳定的标识符（如水印或数据ID），将可验证的证据嵌入其中。生成后，通过检测和验证输出中的这些标识符来完成归因。

为了系统阐明LLM溯源的技术边界和实现逻辑，本节首先统一了这两种基本方法范式的核心定义，并将其应用于所有四个维度（模型、模型结构、训练数据、外部数据）。

首先，将从输入到输出的生成过程形式化如下：令 $x$ 为用户输入， $y$ 为模型生成的输出。从一个模型族中选择一个基础模型实例 $M_{i}$，它通过在训练集 $T$ 上学习获得可训练参数 $\theta$。在推理阶段，除了输入 $x$，还可能引入外部上下文 $E$ （如检索的文档）。因此，整个过程可以表示为对条件生成概率的估计：$P(y\mid x,E,M_{i},T,\theta)$，或等价地写作 $P(y\mid M_{i}(x,E\mid T,\theta))$。

后验溯源的统一-定义

对于给定的输出 $y$，在输入 $x$、外部数据 $E$、训练集 $T$ 和候选模型族 $M$（参数为 $\theta$）的条件下，令 $\mathcal{S}(g,M,\cdot)$ 为溯源函数。后验溯源在没有预先嵌入标记的情况下操作，通过对输出后验分布 $P(y\mid\cdot)$ 的敏感性分析来量化来源。归因源于最大化生成似然或计算基于梯度的影响：


	$\mathcal{S}^{\mathrm{post}}(y,M,\cdot)=\underset{\text{source}}{\operatorname{argmax}}\,\frac{\partial P(y\mid M_{i}(x,E\mid T,\theta))}{\partial{\text{source}}},$

其中 $source$ 可以是模型实例 $M_{i}$、结构组件参数 $\theta_{0}\subset\theta$、训练数据子集 $T_{0}\subset T$ 或外部输入 $E_{0}\subset E$。

模型溯源 (Model Sourcing) 旨在识别最有可能生成特定输出的模型实例。形式化定义为：


	$\mathcal{S}^{\mathrm{post}}_{M}(y,M,\emptyset)=\underset{i}{\operatorname{argmax}}\;P(y\mid M_{i}(x,E\mid T,\theta)),$

模型结构溯源 (Model Structure Sourcing) 通过分析输出后验分布对特定架构组件的梯度敏感性来量化其贡献。形式化表示为：


	$\mathcal{S}^{\mathrm{post}}_{S}(y,M_{s},\emptyset)=\underset{\theta_{0}\in\theta}{\operatorname{argmax}}\;\frac{\partial P(y\mid M(x,E\mid T,\theta))}{\partial\theta_{0}},$

训练数据溯源 (Training Data Sourcing) 通过计算后验概率相对于训练数据分区的梯度来度量单个训练样本对模型输出的因果影响。定义为：


	$\mathcal{S}^{\mathrm{post}}_{T}(y,M,D)=\underset{T_{0}\in T}{\operatorname{argmax}}\;\frac{\partial P(y\mid M(x,E\mid T,\theta))}{\partial T_{0}},$

外部数据溯源 (External Data Sourcing) 通过分析后验输出分布对外部数据变化的敏感性来评估上下文或辅助输入的影响。形式上：


	$\mathcal{S}^{\mathrm{post}}_{E}(y,M,C)=\underset{E_{0}\in E}{\operatorname{argmax}}\;\frac{\partial P(y\mid M(x,E\mid T,\theta))}{\partial E_{0}},$

先验溯源的统一-定义

对于给定的输出 $y$，在输入 $x$、外部数据 $E$、训练集 $T$ 和候选模型族 $M$（参数为 $\theta$）的条件下，令 $\mathcal{S}(g,M,\cdot)$ 为溯源函数。先验溯源在模型训练或内容生成期间嵌入可识别的标记（如水印或签名）。归因通过在生成的输出中检测这些标记并评估其存在的后验概率来执行。

第一步是将标记添加到来源，并应用贝叶斯规则将 $P(y\mid\cdot)$ 重写为 $P(\cdot\mid y)$：


	$$ \begin{split}\mathcal{S}^{\mathrm{prior}}(y,M,\cdot)&=\underset{\text{source}}{\operatorname{argmax}}\,P!\left(y\,\middle	\,M_{i}(x,E\mid T,\theta)+\text{source}^{\prime}\right)\ &=\underset{\text{source}}{\operatorname{argmax}}\,P!\left(M_{i}(x,E\mid T,\theta)+\text{source}^{\prime}\,\middle	\,y\right),\ \end{split} $$

其中 $source'$ 表示嵌入到候选来源中的标记所产生的额外效应。假设主要模型组件和标记组件在给定 $y$ 的条件下是独立的，联合概率可以分解为：


	$\begin{split}\mathcal{S}^{\mathrm{prior}}(y,M,\cdot)=\underset{\text{source}}{\operatorname{argmax}}\,P(M_{i}(x,E\mid T,\theta)\mid y)\cdot\\ P(\text{source}^{\prime}\mid y).\end{split}$

由于 $P(M_{i}(x,E\mid T,\theta)\mid y)$ 在不同候选来源之间近似不变，可以视为常数。因此，决策简化为比较标记的后验概率：


	$\mathcal{S}^{\mathrm{prior}}(y,M,\cdot)=\underset{\text{source}}{\operatorname{argmax}}\,P(\text{source}^{\prime}\mid y).$

这个过程识别出其嵌入标记在生成输出中检测到的后验概率最高的候选来源。

模型溯源 (Model Sourcing) 通过利用预嵌入的先验信息来识别最可能的模型实例，这依赖于对嵌入标记的明确检测：


	$$ \begin{split}\mathcal{S}_{M}^{\text{prior}}(y,M,\emptyset)&=\underset{i}{\operatorname{argmax}}\,P!\left(y\,\middle	\,M_{i}(x,E\mid T,\theta)+M_{i}^{\prime}\right)\ &=\underset{i}{\operatorname{argmax}}\;P(M^{\prime}_{i}\mid y),\end{split} $$

其中 $M^{\prime}_{i}$ 是模型 $M_{i}$ 的嵌入标记。

模型结构溯源 (Model structure sourcing) 通过将特定的架构组件与嵌入的结构标记联系起来量化其贡献：


	$$ \begin{split}\mathcal{S}{S}^{\text{prior}}(y,M{s},\emptyset)&=\underset{\theta_{0}\in\theta}{\operatorname{argmax}}\,P!\left(y\,\middle	\,M_{i}(x,E\mid T,\theta)+\theta_{0}^{\prime}\right)\ &=\underset{\theta_{0}\in\theta}{\operatorname{argmax}}\;P(\theta_{0}^{\prime}\mid y),\end{split} $$

其中 $\theta_{0}^{\prime}$ 是与参数 $\theta_{0}$ 关联的嵌入标记。

训练数据溯源 (Training data sourcing) 通过将输出 $y$ 与嵌入的标记关联起来，追溯其到特定训练样本的因果来源：


	$$ \begin{split}\mathcal{S}{T}^{\text{prior}}(y,M,D)&=\underset{T{0}\in T}{\operatorname{argmax}}\,P!\left(y\,\middle	\,M_{i}(x,E\mid T,\theta)+T_{0}^{\prime}\right)\ &=\underset{T_{0}\in T}{\operatorname{argmax}}\;P(T_{0}^{\prime}\mid y),\end{split} $$

其中 $T_{0}^{\prime}$ 是训练子集 $T_{0}$ 的嵌入标记。

外部数据溯源 (External Data Sourcing) 通过分析与预嵌入标记 $E^{\prime}_{0}$ 的关联来评估上下文或辅助输入的影响：


	$$ \begin{split}\mathcal{S}{E}^{\text{prior}}(y,M,C)&=\underset{E{0}\in E}{\operatorname{argmax}}\,P!\left(y\,\middle	\,M_{i}(x,E\mid T,\theta)+E_{0}^{\prime}\right)\ &=\underset{E_{0}\in E}{\operatorname{argmax}}\;P(E_{0}^{\prime}\mid y),\end{split} $$

其中 $E_{0}^{\prime}$ 是特定外部输入 $E_{0}$ 的标记。