Large Language Monkeys: Scaling Inference Compute with Repeated Sampling

• ArXiv URL: http://arxiv.org/abs/2407.21787v3

• 作者: Quoc V. Le; Ronald Clark; Christopher R’e; Jordan Juravsky; Bradley Brown; Azalia Mirhoseini; Ryan Ehrlich

• 发布机构: Google DeepMind; Stanford University; University of Oxford

---

TL;DR

本文系统地研究了通过重复采样来扩展推理计算（Inference Compute）的方法，发现其能显著提升模型在代码和数学等任务上的覆盖率（即解决问题的能力），其扩展性甚至遵循类似缩放定律的规律，并使得小模型在成本效益更高的情况下超越大模型的单次推理表现。

关键定义

• 重复采样 (Repeated Sampling)：本文的核心技术，指针对一个问题，通过设置正温度（positive temperature）从一个语言模型中独立、多次地生成候选解决方案。
• 覆盖率 (Coverage)：本文核心度量指标，指在生成的所有样本中，至少有一个样本能正确解决问题的比例。在有完美验证器的理想情况下，覆盖率即为模型的最终性能上限。对于编码任务，这等同于 \(pass@k\) 指标。
• 精度 (Precision)：与覆盖率相辅相成的概念，指从生成的众多样本中成功识别出正确答案的能力。这取决于验证器（Verifier）的有效性。
• 验证器 (Verifier)：用于判断一个候选方案是否正确的工具或方法。分为两类：一是自动验证器，如用于代码的单元测试和用于形式化数学的证明检查器；二是在缺乏自动工具时使用的其他方法，如多数投票 (majority voting)和奖励模型 (reward models)。

相关工作

当前大型语言模型（LLM）能力的提升主要依赖于扩展训练计算资源（更大的模型、更多的数据）。然而，在推理阶段，模型通常被限制只对问题进行一次尝试，这成为了一个性能瓶瓶颈。现有工作虽然在数学、编码等领域展示了重复采样的潜力，但缺乏系统性的研究。

本文旨在系统地解决以下问题：

1. 重复采样带来的性能提升（即覆盖率）如何随着样本数量（即推理计算量）的增加而变化？
2. 这种方法的有效性是否能跨越不同的任务、模型尺寸和模型家族？
3. 在没有完美自动验证器的场景下，现有选择方法（如多数投票）的性能表现如何？

本文方法

本文的核心方法是重复采样，其流程非常简洁：

1. 生成：针对一个给定的问题，通过从一个LLM（设置温度 \(T>0\) 以确保多样性）中独立采样，生成 \(k\) 个候选解决方案。
2. 验证：使用一个特定领域的验证器（例如，编码任务的单元测试）来评估所有 \(k\) 个样本，并从中选出一个最终答案。

图1：本文遵循的重复采样流程。1) 通过正温度从LLM中为给定问题生成多个独立的候选解决方案。2) 使用领域特定的验证器（例如，代码的单元测试）从生成的样本中选择最终答案。

本文的重点并非发明这一技术，而是对其进行系统性的量化研究，并揭示其内在规律和实用价值。

创新点

本文的创新之处在于将推理计算视为一个可扩展的维度，类似于训练计算，并首次系统地刻画了其“缩放定律”。

1. 实证有效性：本文在多个任务（GSM8K, MATH, MiniF2F, CodeContests, SWE-bench Lite）和多种模型（Llama, Gemma, Pythia系列，参数从70M到70B）上进行了大规模实验，一致性地证明了重复采样的有效性。覆盖率随着样本数量的增加（跨越四个数量级）而平滑提升。
2. 成本效益：通过重复采样，一个较弱但成本较低的模型可以超越一个更强但昂贵的模型单次采样的性能。例如，在SWE-bench Lite任务上，使用DeepSeek-Coder-V2-Instruct采样250次，问题解决率达到56%，超过了使用GPT-4o和Claude 3.5 Sonnet混合的单次采样SOTA（43%），且成本更低。

推理缩放定律

本文发现覆盖率和样本数量之间的关系存在可预测的规律，提出了推理时缩放定律（inference-time scaling laws）的可能性。

1. 指数化幂律模型：覆盖率 \(c\) 与样本数 \(k\) 的关系可以用一个指数化的幂律函数来很好地拟合：

   \[c \approx \exp(ak^{b})\]

   其中 \(a\) 和 \(b\) 是拟合参数。这个模型表明，在很多情况下，覆盖率的对数与样本数 \(k\) 近似成幂律关系，尤其当 \(b\) 接近0时，覆盖率近似于与样本数的对数呈线性关系。

   

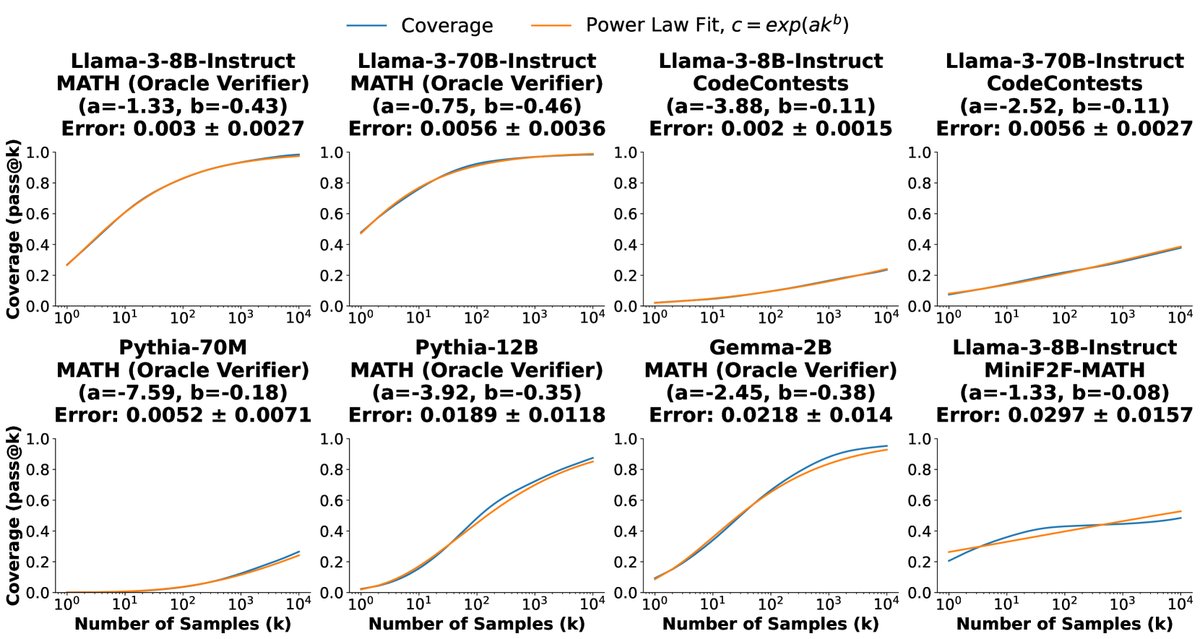
   图5：在大多数任务和模型中，覆盖率和样本数之间的关系可以用指数化幂律来建模。图中也突显了一些不完全符合此趋势的曲线，如Llama-3-8B-Instruct在MiniF2F-MATH上的表现。

2. 模型族内曲线相似性：在同一个模型家族中（如Llama-3系列），不同大小模型的覆盖率曲线（在对数x轴上）呈现出相似的S形，但具有不同的水平偏移。这意味着，更强的模型只需更少的样本就能达到与较弱模型相同的覆盖率水平，但提升的“加速度”是相似的。

   

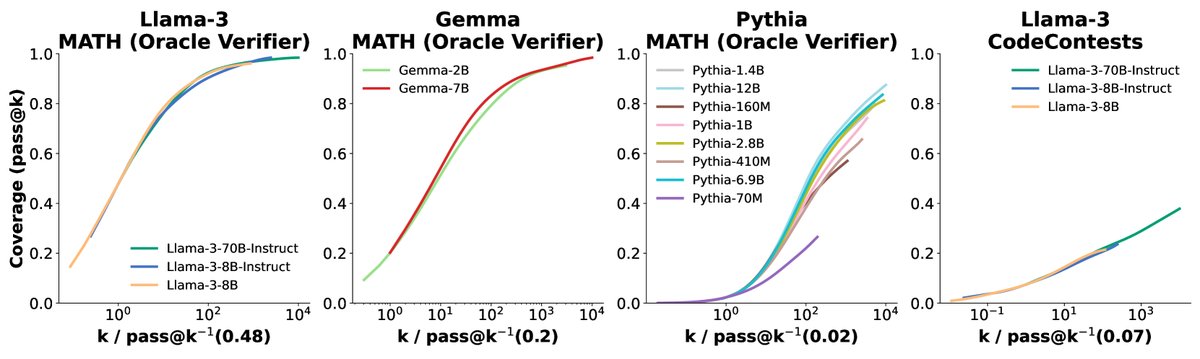
   图6：通过水平移动（在对数尺度上）将同一家族不同模型的覆盖率曲线对齐。这种对齐后的曲线相似性表明，在同一模型家族内，覆盖率的扩展遵循相似的形状。

实验结论

关键实验结果

本文的实验有力地验证了重复采样的优势和局限性。

1. 覆盖率显著提升：在所有五个测试任务（包括数学、形式化证明、编程竞赛和真实世界软件修复）和几乎所有模型上，覆盖率都随着样本数量的增加而持续增长。例如，在CodeContests任务上，Gemma-2B的覆盖率从 \(pass@1\) 的0.02%提升到 \(pass@10k\) 的7.1%，增长超过300倍。

   

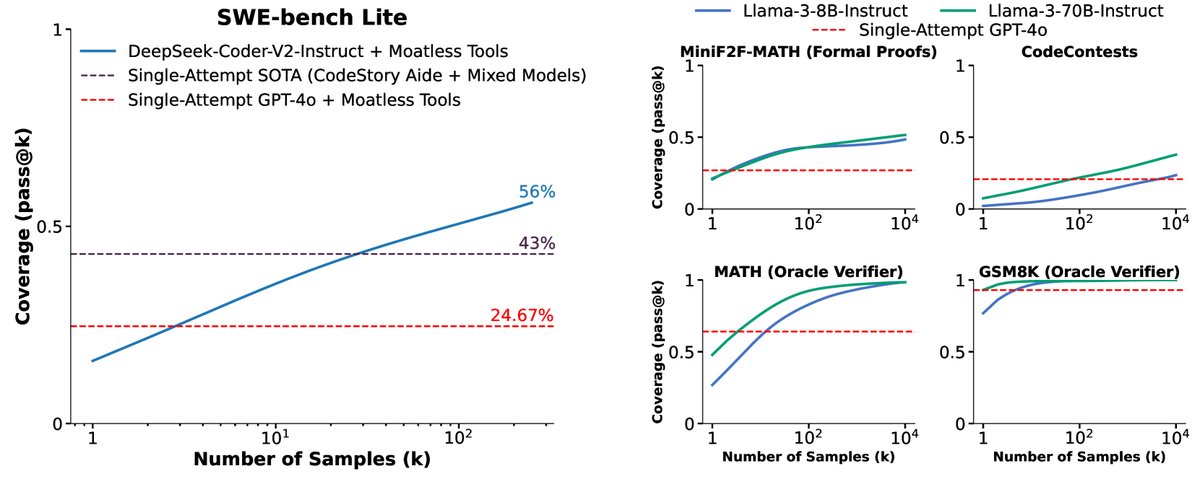
   图2：在五个任务中，覆盖率（至少一个生成样本解决问题的比例）随着样本数量的增加而增加。值得注意的是，在SWE-bench Lite上，通过重复采样，一个开源方法的解决率从15.9%提高到了56%。

2. 成本性能权衡：实验证明，在固定计算成本（FLOPs）的情况下，选择“小模型+多样本”还是“大模型+少样本”取决于具体任务。在MATH和GSM8K任务上，Llama-3-8B始终比70B模型更具成本效益；但在CodeContests任务上，70B模型几乎总是更优选择。在API成本方面，DeepSeek-Coder-V2在SWE-bench Lite上用5次采样的成本不到GPT-4o或Claude 3.5 Sonnet单次采样的三分之一，但解决的问题更多。

   

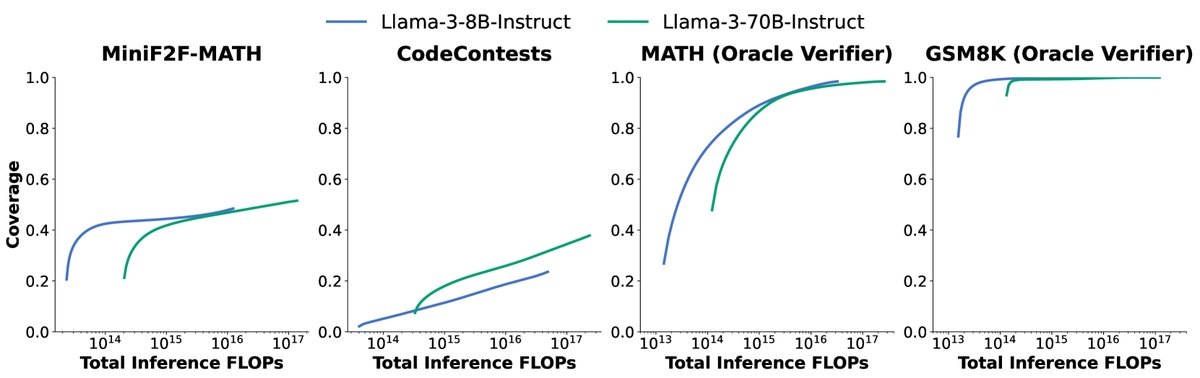
   图4：比较Llama-3-8B-Instruct和Llama-3-70B-Instruct在成本（推理FLOPs）和覆盖率上的表现。理想的模型大小取决于任务、计算预算和覆盖率要求。

   模型	每次尝试成本 (USD)	尝试次数	解决的问题 (%)	总成本 (USD)	相对总成本
   DeepSeek-Coder-V2-Instruct	0.0072	5	29.62	10.8	1x
   GPT-4o	0.13	1	24.00	39	3.6x
   Claude 3.5 Sonnet	0.17	1	26.70	51	4.7x

   表1：在SWE-bench Lite数据集上使用Moatless Tools智能体框架时，不同模型的API成本（美元）与性能对比。通过增加采样次数，开源的DeepSeek-Coder-V2-Instruct能以不到闭源前沿模型三分之一的价格，达到更高的 问题解决率。

3. 验证器的瓶颈：在没有自动验证器的任务（如MATH和GSM8K）上，常用验证方法（多数投票、奖励模型）的性能在样本数达到约100次后就基本饱和，无法跟上持续增长的覆盖率。这导致了理论上限（覆盖率）与实际性能之间的差距越来越大，验证器无法在大量错误样本中“大海捞针”。

   

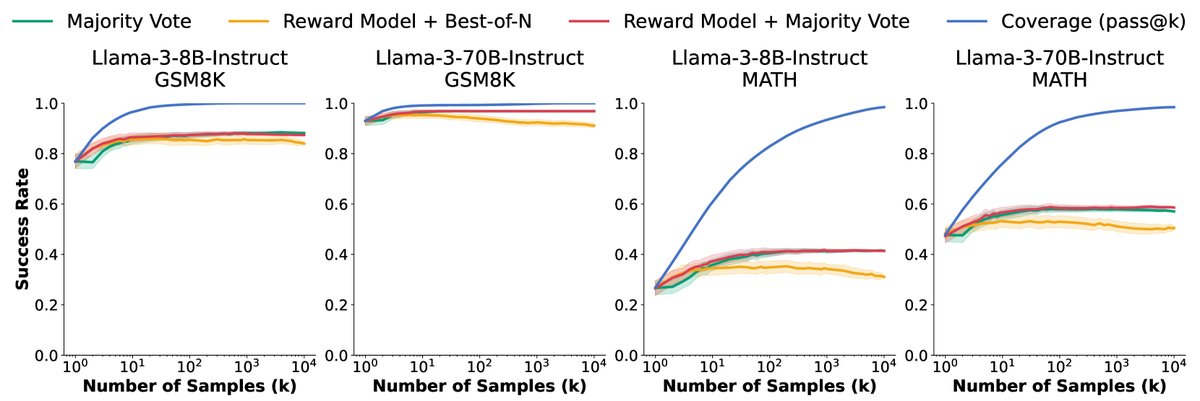
   图7：随着样本数增加，覆盖率（理想验证器性能）与主流选择方法（多数投票、奖励模型）性能的对比。尽管覆盖率接近完美，但所有样本选择方法的性能在达到100个样本前就已饱和，未能触及覆盖率上限。

总结

本文的最终结论是，通过重复采样来扩展推理计算是一种强大且有效的提升模型性能的策略，特别是在拥有可靠自动验证器的领域（如编程）。它为在性能和成本之间进行权衡提供了新的自由度。然而，该方法的潜力在许多任务中受到了验证器能力的严重制约。因此，未来的研究重点应放在开发更强大的、可扩展的验证方法上，以充分释放重复采样的威力。