Learning When to Plan: Efficiently Allocating Test-Time Compute for LLM Agents

• ArXiv URL: http://arxiv.org/abs/2509.03581v1

• 作者: Jack Parker-Holder; Edward Grefenstette; Jonathan Cook; Tim Rocktäschel; Jens Tuyls; Bartłomiej Cupiał; Ulyana Piterbarg; Davide Paglieri

• 发布机构: IDEAS NCBR; New York University; Princeton University; University College London; University of Oxford; University of Warsaw

---

TL;DR

本文提出了一种两阶段训练方法（监督微调+强化学习），使大型语言模型（LLM）智能体能够学习在序贯决策任务中动态地决定何时进行规划，从而以更高效的计算成本实现更优的性能和更强的可控性。

关键定义

本文提出了一个用于动态规划的 conceptual framework (概念框架)，其核心定义如下：

1. 动态规划智能体 (Dynamic Planning Agent)：这是一种能够根据当前状态的需要，灵活决定是否分配测试时计算资源 (test-time compute) 进行规划的智能体。它摒弃了“总是规划”或“从不规划”的固定策略，寻求一种更高效的决策模式。

2. 概念性策略分解：本文将单一LLM的行为概念上分解为三个协同工作的策略，它们通过统一的输出格式实现：
   • 决策策略 (Decision Policy, $\phi_{\theta}$): 判断当前是否需要生成新计划。这通过模型是否选择输出 \(<plan>\) 标志来隐式实现。
   • 规划策略 (Planning Policy, $\psi_{\theta}$): 当决定要规划时，生成新的自然语言计划 $p_t$。
   • 行动策略 (Acting Policy, $\pi_{\theta}$): 根据当前上下文和计划（新生成的或已有的）来生成具体行动 $a_t$。

3. 规划优势 (Planning Advantage, $A_{plan}$)：指生成一个新计划所带来的预期未来回报的提升量，与继续使用旧计划相比。其定义为：

   \[A_{plan}(c_{t})=\mathbb{E}_{p_{t}\sim\psi_{\theta}(\cdot\mid c_{t},d_{t}=1)}[V^{\pi_{\theta}}(c_{t},p_{t})-V^{\pi_{\theta}}(c_{t},p_{t-1})]\]

   其中 $V^{\pi_{\theta}}(c_t, p_t)$ 是在给定上下文 $c_t$ 和计划 $p_t$ 下的预期未来回报。

4. 规划成本 (Cost of Planning, $C_{plan}$)：规划行为带来的总成本，包括：

   \[C_{plan}=C_{tokens}+C_{latency}+C_{noise}\]
   • 计算成本 ($C_{tokens}$): 生成计划所耗费的 token 数量。
   • 延迟成本 ($C_{latency}$): 规划所花费的真实时间，在本文的实验环境中可忽略。
   • 不稳定性成本 ($C_{noise}$): 过度或不一致的重新规划可能导致行为不稳定（如目标摇摆、无效回溯），从而降低任务成功率。这是一个概念性成本，其负面影响会通过降低任务回报而间接被优化。
5. 计划漂移 (Plan Drift)：指随着智能体与环境交互，现有计划的有效性随时间推移而衰减的现象。计划的抽象层次、模型的准确性和环境的动态性都会影响漂移速度。这个概念解释了为何智能体需要周期性地重新评估是否需要规划。

相关工作

当前，在序贯决策领域，相关工作主要分为两类。一类是经典的规划方法，如蒙特卡洛树搜索 (Monte Carlo Tree Search, MCTS) 和模型预测控制 (Model Predictive Control, MPC)，它们强调在行动前进行显式展望。另一类是大型语言模型（LLM）的推理方法，如 ReAct，它通过提示词引导模型在每一步行动前都进行思考和规划。

然而，现有方法存在一个关键瓶颈：“总是规划”的策略在计算上是昂贵的，并且在长时序任务中可能因引入行为不稳定性而降低性能；而“从不规划”则限制了智能体解决复杂问题的能力。目前缺乏一种有效的方法，能让LLM智能体学会在何时分配宝贵的测试时计算资源（即规划）是真正有益的。

本文旨在解决这个具体问题：如何训练LLM智能体，使其能够在序贯决策任务中学会动态、高效地分配测试时计算资源，即学会“何时应该规划”。

本文方法

本文的核心方法是提出一个概念框架，并基于此设计了一个两阶段训练流程，以教会LLM智能体动态规划。

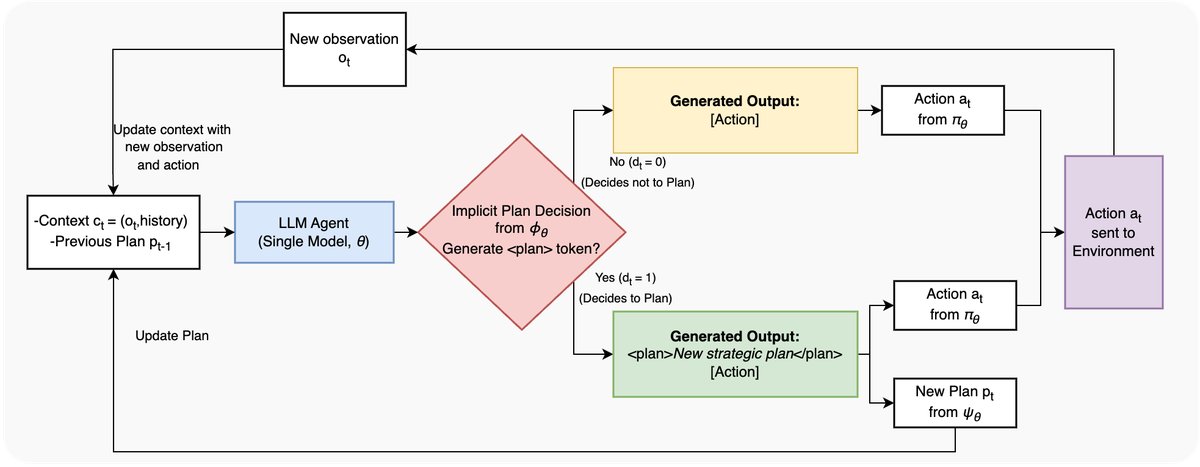图2：动态规划智能体架构。智能体是一个单一、整体的LLM，其概念性策略通过统一的输出格式实现。规划决策（$\phi_{\theta}$）由模型选择是否以 \(<plan>\) 标志开始其生成来隐式做出。这个单一输出字符串随后被解析以提取动作（$a_{t}$）和（如果存在的话）新计划（$p_{t}$），从而执行行动（$\pi_{\theta}$）和规划（$\psi_{\theta}$）策略。

概念框架与优化目标

本文将智能体的决策过程建模为一个成本效益分析：仅当规划带来的预期收益（规划优势 $A_{plan}$）超过其总成本（规划成本 $C_{plan}$）时，才触发规划行为。

为了让智能体隐式地学会这种权衡，本文设计了一个强化学习目标。智能体的参数 $\theta$ 通过最大化以下目标函数进行优化：

\[\theta^{\*}=\arg\max_{\theta}\mathbb{E}_{\tau\sim\theta}\left[\sum_{t=0}^{H}\gamma^{t}\left(R_{task}(s_{t},a_{t})-d_{t}\cdot C_{tokens,t}\right)\right]\]

其中，$R_{task}$ 是环境提供的任务奖励，$d_{t}$ 是一个二元变量（如果第 $t$ 步进行了规划则为1，否则为0），$C_{tokens,t}$ 是规划产生的 token 数量的成本。这个目标函数直接鼓励智能体在任务回报的提升（隐式地代表了 $A_{plan}$）和规划的计算成本之间做出权衡。而由频繁规划导致的行为不稳定等负面效应（即 $C_{noise}$）会自然地导致任务回报降低，从而被间接惩罚。

两阶段训练流程

为了实现上述目标，本文提出一个包含监督微调（SFT）和强化学习（RL）的两阶段训练流程：

第一阶段：监督微-调预训练 (SFT Priming)

• 目的：为后续的RL阶段“预热”模型，提前注入多样化的规划行为模式。这对于能力有限的较小模型尤其重要，因为它们难以从零开始生成高质量的规划。
• 数据生成：使用一个强大的教师模型（Llama-3.3-70B），在 \(Crafter\) 环境中生成带有规划的轨迹数据。为了保证数据多样性，教师模型被设置为以随机频率（例如每2到12步）进行规划。
• 训练：在一个较小的学生模型（Llama-3.1-8B）上进行SFT。训练数据的格式是关键：如果教师模型在某一步进行了规划，则训练目标是 \("<plan> [计划内容] </plan> [行动]"\)；否则，目标就是简单的 \("[行动]"\)。通过这种方式，模型学会了动态规划的输出格式和基本能力。

第二阶段：强化学习微调 (RL Fine-Tuning)

• 目的：在真实环境中通过与环境交互来进一步优化和提炼动态规划能力，使其真正服务于最大化长期任务回报。
• 算法：采用近端策略优化 (Proximal Policy Optimization, PPO) 算法。
• 训练：使用SFT预训练过的模型作为初始模型，在 \(Crafter\) 环境中进行RL训练。优化目标如上文公式所述，旨在最大化任务奖励，同时惩罚规划的 token 成本。通过这种方式，智能体学会了在“规划以获得更高回报”和“不规划以节省成本”之间进行动态决策。

创新点

• 从固定到动态：本文最核心的创新在于，将智能体规划从固定的、启发式的策略（如“总是规划”或“每k步规划”）转变为一个通过学习获得的、适应环境的动态决策过程。
• SFT+RL训练范式：提出的两阶段训练流程证明了 SFT预训练对于教会较小模型掌握复杂动态规划技能的关键作用。SFT提供了必要的“规划先验知识”，而RL则在此基础上进行优化和提炼。
• 概念与实践结合：通过引入“不稳定性成本”等概念，为“为何过度规划有害”提供了理论解释，并通过RL目标函数将其与实际训练相结合，使得智能体能够隐式地学习到这种复杂的权衡。

实验结论

本文通过在 \(POGS\) 和 \(Crafter\) 环境中的一系列实验，验证了动态规划的有效性。

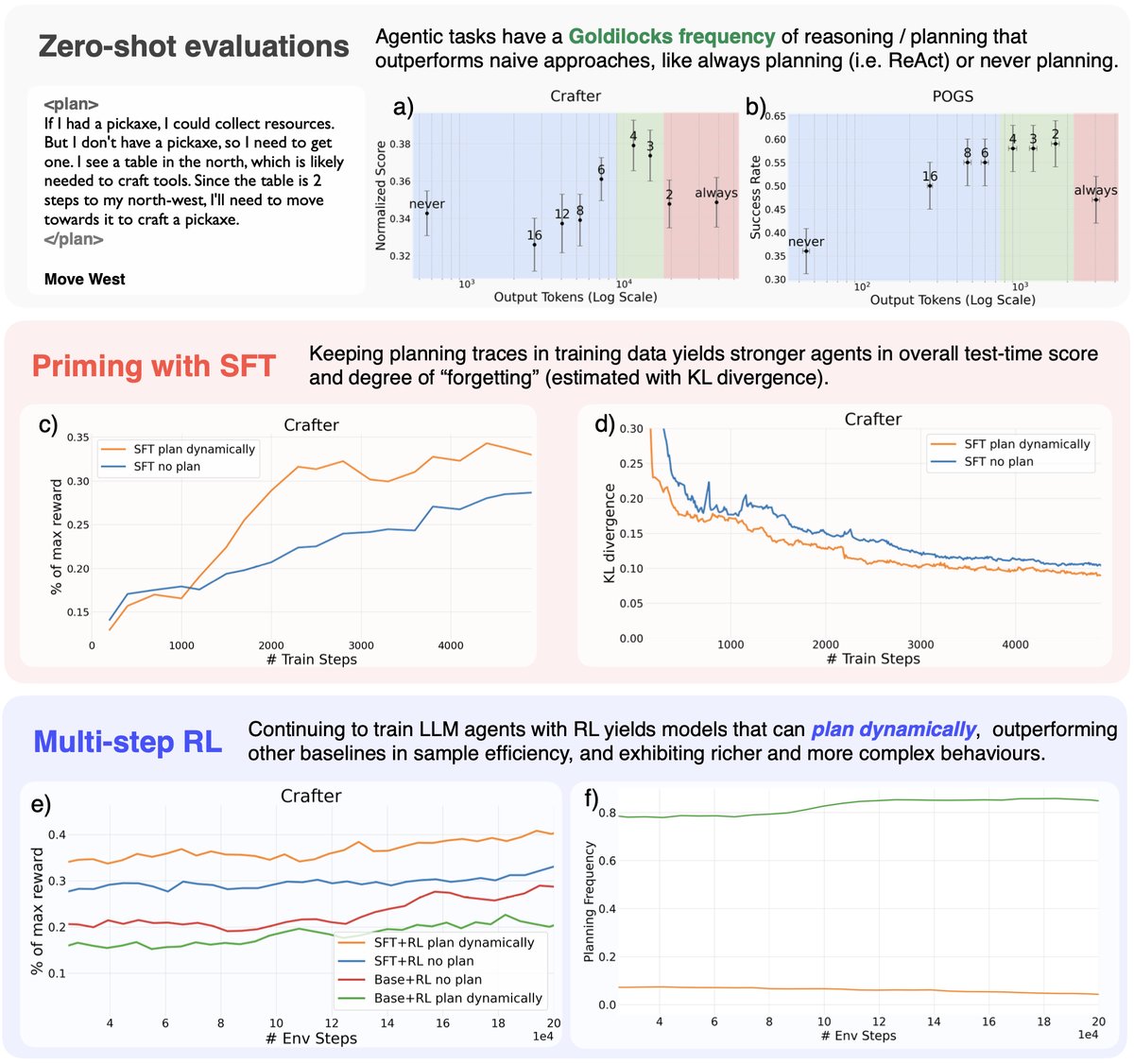图1：(a-b) Zero-shot结果显示，在Crafter和POGS中存在最佳的“金发姑娘”规划频率。(c-d) SFT结果表明，规划智能体在与基础模型的KL散度较低时表现更佳。(e-f) RL结果显示，经过SFT预训练的规划智能体比非规划基线更具样本效率，并能更稳定地达成复杂目标。

Zero-Shot 评估结论:

• “金发姑娘”效应 (Goldilocks Effect)：在未使用任何微调的大模型 (Llama-3.3-70B) 上进行测试发现，无论是“总是规划”（类似ReAct）还是“从不规划”，性能都不是最优的。最佳性能出现在一个中间的规划频率（如在Crafter中每4步规划一次）。
• 过度规划的危害：过于频繁的规划不仅计算成本高，还会引入行为不稳定性（如在POGS中更多的回溯），导致性能下降。这证实了本文框架中“不稳定性成本” ($C_{noise}$) 的存在。

SFT 预训练结论:

• 在SFT阶段，使用包含显式自然语言计划的数据进行训练的智能体（\(Primed-Dynamic\)），其性能始终优于在完全相同的行动序列上、但去除了计划文本后进行训练的智能体（\(Primed-Naive\)）。这表明，计划本身就是一种有效的学习信号，它为行动提供了上下文和解释，有助于模仿学习过程。

RL 微调结论:

• SFT预训练至关重要：\(SFT+RL\) 版本的动态规划智能体在样本效率和最终性能上显著优于从头开始训练的 \(Base+RL\) 智能体。这表明对于中等规模的模型（8B），SFT提供的先验知识对于学会有效规划是必不可少的。
• 动态规划的优势：\(SFT+RL plan dynamically\) 智能体在训练初期表现出更高的样本效率，并能学会生成多层次的抽象计划以及在需要时进行重新规划。
• 人类协作与可控性：经过RL训练后，动态规划智能体能够很好地理解并遵循人类提供的外部计划。在一个案例中，通过人类提供高级计划进行引导，智能体成功完成了整个Crafter任务（采集到钻石），达到了自主智能体无法企及的高度，极大地展示了其可控性和协作潜力。

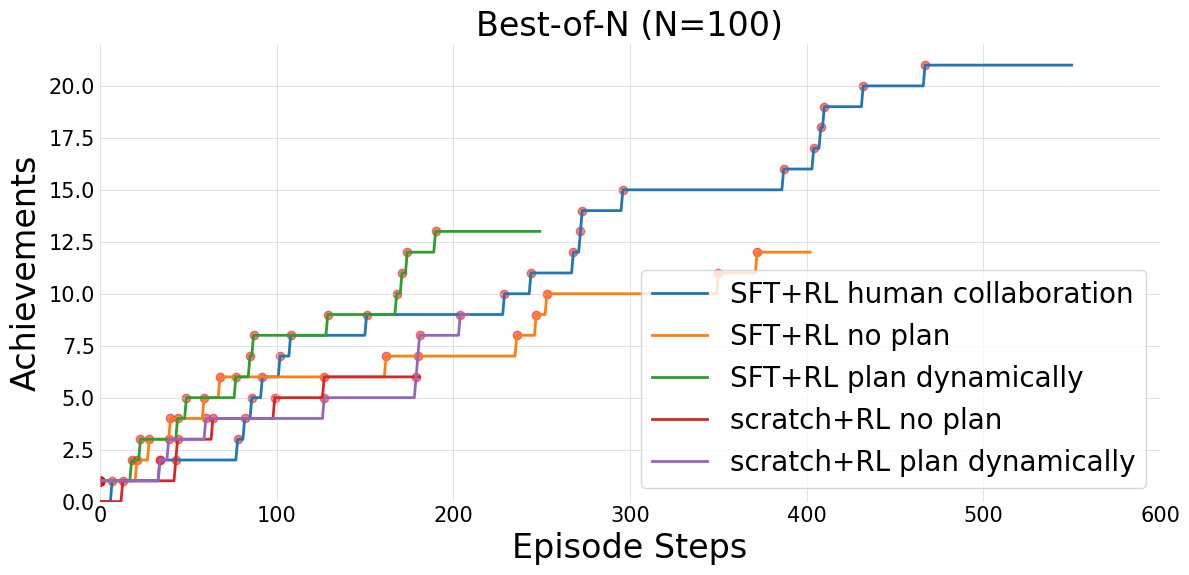图5：“最好中的最好”（Best-of-N，N=100）在Crafter上的比较图。结果显示，人类协作（N=20）取得了最强的进展，其次是SFT+RL动态规划和SFT+RL无规划，而基础RL基线则表现落后。

最终结论: 实验证明，训练LLM智能体动态地决定何时规划，相比于固定的规划策略，是一种更有效、更高效的方法。本文提出的两阶段SFT+RL训练范式是实现这一目标的有效路径，它不仅提升了智能体的自主性能和效率，还增强了其与人类协作的可控性，为构建更强大、更安全的智能体系统开辟了新的方向。