Less is More Tokens: Efficient Math Reasoning via Difficulty-Aware Chain-of-Thought Distillation
-
ArXiv URL: http://arxiv.org/abs/2509.05226v1
-
作者: Bhiksha Raj; Abdul Waheed; Deva Ramanan; Chancharik Mitra
-
发布机构: Carnegie Mellon University
TL;DR
本文提出了一种困难度感知的思维链蒸馏框架，通过在与问题难度成比例的思维链（CoT）数据上进行后训练，教会大语言模型根据问题复杂性动态调整推理深度，从而在保持或提升准确率的同时，显著提升推理效率。
关键定义
- 困难度感知推理 (Difficulty-Aware Reasoning): 指模型根据输入问题的内在复杂性，动态调整其推理过程的深度和详细程度的能力。对于简单问题，模型应生成简洁的推理步骤；对于复杂问题，则应生成更详尽的推理链。
- 困难度感知的思维链蒸馏 (Difficulty-Aware Chain-of-Thought Distillation): 本文提出的核心框架。它采用“教师-学生”模式，首先由一个强大的教师模型生成详尽但冗长的思维链，然后根据一个预估的难度分数对这些思维链进行压缩，最后用这些压缩后的、长度与难度匹配的数据来训练（蒸馏）一个学生模型。
- 混合训练 (Hybrid Training, SFT + DPO): 本文验证的最有效训练策略。它结合了监督微调（Supervised Fine-Tuning, SFT）和直接偏好优化（Direct Preference Optimization, DPO）。SFT首先让模型学习模仿压缩后推理链的结构和风格（简洁性），随后DPO通过对比学习（将压缩的短推理作为偏好项，原始长推理作为拒绝项）进一步提升模型的推理准确率。
相关工作
当前，通过思维链（Chain-of-Thought, CoT）提示增强大语言模型（LLM）的多步推理能力已成为主流范式。然而，现有CoT方法的一个关键瓶颈是，无论问题难度如何，模型生成的推理轨迹通常都过于冗长，导致了不必要的“过度思考”（over-thinking），增加了推理延迟和计算成本。
虽然已有研究尝试通过强化学习、固定预算或外部路由机制来控制推理长度，但这些方法未能让模型内在地学会根据任务的复杂性来调整自身的推理策略。
本文旨在解决这一具体问题：如何训练模型，使其能够像人类一样，根据问题的内在难度自适应地分配认知资源，即对简单问题进行最少化推理，对复杂问题进行深入思考，从而实现推理效率和准确性的平衡。
本文方法
本文提出了一个通用的困难度感知思维链（CoT）蒸馏框架，旨在让模型能够根据问题难度自适应地调整推理的详细程度。该框架包含数据生成和模型训练两个主要阶段。
数据生成
数据生成流程的目标是创建与问题难度相匹配的训练样本。
- 困难度评估：首先，使用一个大型语言模型（GPT-4o-mini）作为评分器，为每个数学问题 $x_i$ 评估一个1到10级的难度分数 $d(x_i)$。该评分标准与AoPS（Art of Problem Solving）竞赛的难度等级对齐，以确保评估结果的稳定性和与人类感知的对齐。
- 困难度感知的压缩：对于一个由高能力教师模型生成的原始冗长推理链 $r_i^{\text{long}}$，本文设计了一个基于提示的压缩函数 $s(r_i^{\text{long}}, d(x_i))$，它会根据难度分数 $d(x_i)$ 将 $r_i^{\text{long}}$ 压缩成一个更简洁的版本 $\tilde{r}_i$。难度越低，压缩程度越高。这个过程旨在保留核心逻辑的同时，去除冗余步骤。
通过该流程，为单模态（来自OpenMathReasoning数据集）和多模态（来自LLaVA-CoT-100K数据集）任务生成了训练数据。如下表所示，压缩比率（CR）与问题难度和模态相关。
| 难度等级 | CR (单模态) | CR (多模态) |
|---|---|---|
| 1 | 79.1 | 49.9 |
| 2 | 84.5 | 47.6 |
| 3 | 87.0 | 43.6 |
| 4 | 88.0 | 40.6 |
| 5 | 88.8 | 35.1 |
| 6 | 89.4 | 29.7 |
| 7 | 90.5 | 16.9 |
| 8 | 90.6 | NA |
| 9 | 90.4 | NA |
| 10 | 88.8 | NA |
Table 1: 单模态和多模态任务中不同难度等级的压缩率（%）。更高的值表示推理长度的缩减更大。
模型训练
在获得与难度对齐的训练数据后，本文使用一种混合策略来训练学生模型，旨在让其内化困难度感知的推理行为。
监督微调 (SFT)
作为训练的第一阶段，SFT通过最小化交叉熵损失来直接教模型模仿压缩后的推理轨迹 $\tilde{r}_i$：
\[\min_{\theta} \mathcal{L}_{\text{SFT}} = \sum_{i=1}^{N} \text{CE}(f_{\theta}(x_i), \tilde{r}_i)\]这一步主要让模型学习根据问题复杂性生成相应风格和长度的推理。
直接偏好优化 (DPO)
为了进一步提升推理的准确性，本文应用DPO进行第二阶段的训练。在此阶段，压缩后的简洁推理 $\tilde{r}_i$ 被视为“偏好”（preferred）的回答，而原始的冗长推理 $r_i^{\text{long}}$ 则被视为“拒绝”（rejected）的回答。DPO通过优化以下目标来训练模型：
\[\min_{\theta} \mathcal{L}_{\text{DPO}} = -\sum_{i=1}^{N} \log \frac{\exp\left(\beta \cdot \text{KL}(f_{\theta}(x_i), \tilde{r}_i)\right)}{\exp\left(\beta \cdot \text{KL}(f_{\theta}(x_i), \tilde{r}_i)\right) + \exp\left(\beta \cdot \text{KL}(f_{\theta}(x_i), r_i^{\text{long}})\right)}\]这一步明确地教导模型偏爱高效简洁的推理，而不是冗长的表述，从而在保持准确性的前提下优化输出。
混合训练 (SFT + DPO)
本文发现，先进行SFT再进行DPO的混合训练课程效果最好。SFT使模型首先掌握与难度相关的推理模式，DPO则通过对比学习进一步优化和提炼这种能力，最终在准确性和效率之间取得了最佳平衡。
实验结论
主要发现
- SFT学习长度与格式：单独使用SFT进行训练，模型能有效地学习生成与目标（压缩后的）推理链长度和格式相似的输出，但往往以牺牲最终答案的准确性为代价。
- DPO学习推理准确率：单独使用DPO训练，模型在推理准确率上表现优异，通常能达到或超过基线模型的水平，但在减少推理长度（即提升效率）方面效果有限，输出仍然较为冗长。
- SFT+DPO兼顾长度与正确性：结合SFT和DPO的混合训练策略取得了最佳的平衡。该方法能将推理长度（Token使用量）减少高达30%，同时保持甚至提高最终答案的准确率。SFT教会模型“如何说得简洁”，而DPO则教会模型“如何说得正确”，二者互为补充。
实验结果
单模态
如下表所示，对于文本数学推理任务，SFT+DPO训练的模型（R1-Distill-Qwen）在多个基准测试中，其性能与基线模型相当或更优，同时显著减少了平均Token使用量。例如，7B模型在保持AIME性能的同时，Token消耗减少了10%；在MATH上，准确率甚至更高，Token消耗也更少。
| 模型设置 | AIME | AMC | Math | GSM8K | HMMT |
|---|---|---|---|---|---|
| Base | |||||
| R1-Distill-Qwen-1.5B | 20.0 (6768) | 54.2 (5381) | 77.0 (3588) | 83.9 (1660) | 12.2 (7176) |
| R1-Distill-Qwen-7B | 35.0 (6360) | 71.1 (4723) | 86.0 (3050) | 88.0 (553) | 24.4 (6876) |
| Thinking | |||||
| L1-Qwen-1.5B-Max | 24.4 (2280) | 67.5 (1976) | 83.6 (1693) | 87.3 (1479) | 11.1 (2272) |
| Nemotron-1.5B | 33.3 (6692) | 62.7 (5186) | 83.0 (3419) | 75.9 (2965) | 14.4 (7751) |
| Nemotron-7B | 31.7 (6770) | 62.7 (5196) | 86.2 (3112) | 89.7 (1850) | 28.9 (6969) |
| R1-Distill-Qwen-1.5B | |||||
| SFT | 5.0 (1081) | 38.6 (699) | 65.2 (526) | 77.6 (241) | 0.0 (845) |
| DPO | 18.4 (6964) | 50.6 (5524) | 74.6 (3864) | 82.9 (1733) | 10.0 (7388) |
| SFT + DPO | 23.4 (6192) | 57.8 (4893) | 79.4 (3269) | 82.3 (1527) | 12.2 (6458) |
| R1-Distill-Qwen-7B | |||||
| SFT | 8.4 (864) | 51.8 (789) | 75.4 (474) | 88.5 (244) | 2.2 (808) |
| DPO | 25.0 (6584) | 62.7 (4932) | 86.0 (3062) | 89.2 (592) | 17.8 (6940) |
| SFT + DPO | 31.7 (5724) | 69.9 (4251) | 88.8 (2745) | 86.9 (498) | 20.0 (6188) |
Table 2: 单模态模型在七个数学推理基准上的性能。每个单元格报告 Pass@1 准确率，括号内为平均Token数。本文提出的SFT+DPO模型在多数基准上与基线或单独微调的模型性能相当或更优，同时生成更短的推理轨迹。
多模态
在多模态（视觉语言）任务中，观察到类似趋势。如下图所示，SFT+DPO训练的7B模型在所有基准测试中均取得了最高的准确率，同时其平均Token使用量比教师模型（Qwen2.5-VL-7B）减少了10%以上，比SFT模型略高，但远低于DPO模型和基线模型。这证明了该方法在多模态场景下同样能在效率和效果之间取得良好平衡。
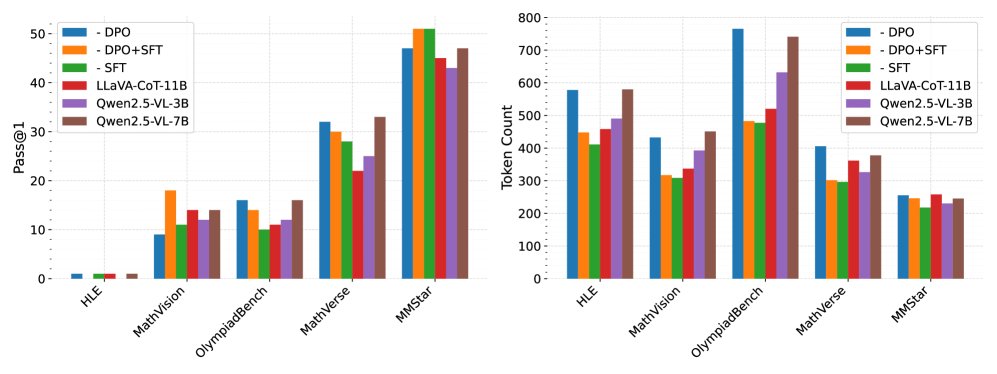Figure 1: 左图展示了Pass@1准确率，右图展示了多模态基准上推理输出的平均Token数。SFT、DPO和SFT+DPO是我们在Qwen-2.5-VL-7B-Instruct基础上训练的模型。
定性评估 (LLM-as-Judge)
通过使用GPT-4o-mini作为“法官”对模型生成的推理轨迹进行定性评估，结果进一步验证了上述结论。SFT+DPO模型在清晰度、完整性、正确性和冗余度四个维度上获得了最均衡的高分。如下图所示，无论是在单模态还是多模态设置中，SFT+DPO都显著优于基线模型和其他训练策略，生成的推理链不仅准确，而且结构清晰、易于理解。
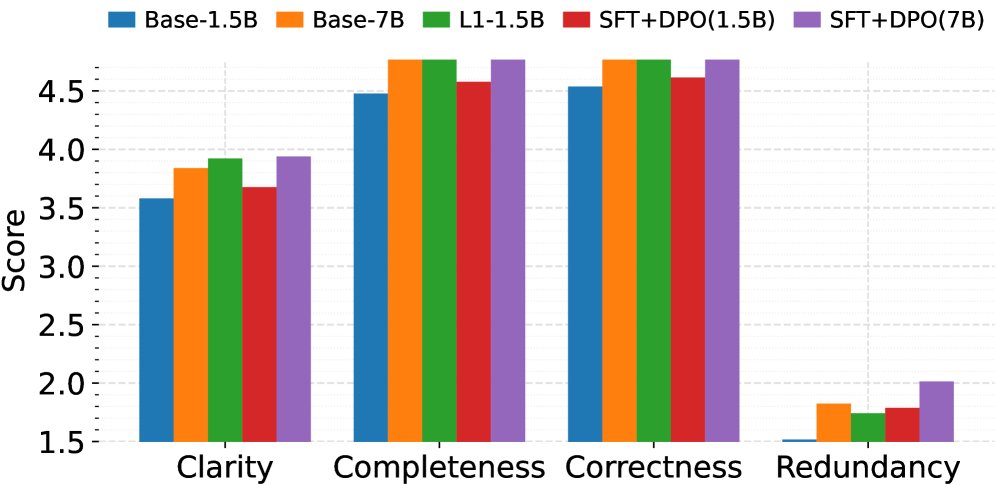((a)) 单模态
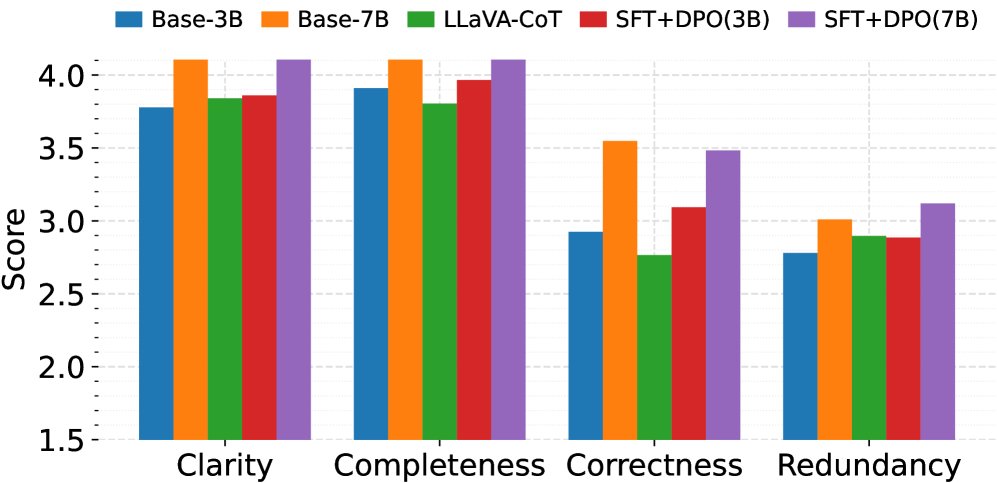((b)) 多模态
Figure 2: 单模态和多模态模型的LLM-as-Judge评估分数。评估基于清晰度、正确性、完整性和冗余度四个定性标准，使用1-5分制由GPT-4o-mini打分。SFT+DPO在内容质量和格式方面均一致优于基线模型。
总结
本文提出的困难度感知CoT蒸馏框架，特别是结合SFT和DPO的混合训练策略，成功地训练出能够根据问题难度自适应调整推理深度的模型。这些模型不仅解决了现有CoT方法“过度思考”的效率问题，实现了高达30%的推理长度缩减，而且在多数情况下保持甚至提升了最终答案的准确率。这为构建更高效、更智能、更具可解释性的推理智能体开辟了新的方向。