LIMO: Less is More for Reasoning
-
ArXiv URL: http://arxiv.org/abs/2502.03387v1
-
作者: Yixin Ye; Yang Xiao; Ethan Chern; Zhen Huang; Shijie Xia; Pengfei Liu
-
发布机构: GAIR; SII; Shanghai Jiao Tong University
TL;DR
本文提出并验证了LIMO假说：对于在预训练中已编码了丰富领域知识的基础模型，仅需极少量（本文为817个）精心策划的认知过程范例（高质量的推理链），便能有效激发其复杂的数学推理能力，从而以不到1%的训练数据量，在多个高难度基准上超越了依赖大规模数据微调的SOTA模型。
关键定义
- LIMO假说 (Less-Is-More Reasoning Hypothesis): 在预训练阶段已充分编码领域知识的基础模型中，复杂的推理能力可以通过少量但经过精确编排的认知过程演示来激发。
- 激发阈值 (Elicitation Threshold): 激活模型复杂推理能力的临界点。该阈值并非由目标任务的复杂性决定，而是由两个关键因素决定：（1）模型在预训练中编码的知识基础的完备性；（2）作为“认知模板”的训练后样本的有效性，这些样本向模型展示了如何有效利用其现有知识库。
- 认知模板 (Cognitive Templates): 指那些高质量的、用于训练后微调的样本。它们的作用是向模型展示如何系统性地利用其已有的知识来解决复杂的推理任务，本质上是激活模型潜力的“钥匙”。
相关工作
当前，提升大语言模型（LLMs）复杂推理能力的主流范式是依赖大规模的训练数据，通常需要数万甚至数十万个样本进行监督微调（Supervised Fine-tuning, SFT）。这种方法的背后有两个基本假设：一是掌握复杂认知过程需要大量的监督演示；二是SFT主要导致模型记忆而非真正的泛化能力。这一范式不仅带来了高昂的数据收集和计算成本，其必要性也值得怀疑。
本文旨在解决的问题是：能否用一种更高效、数据量更少的方式来激发LLMs中已有的、但处于潜伏状态的复杂推理能力？
本文认为，两大技术革命为解决此问题创造了条件：
- 知识基础革命：现代基础模型在预训练阶段吸收了前所未有的海量数学内容，使得模型参数中已蕴含丰富的数学知识。挑战从“知识获取”转变为“知识激发”。
- 推理时计算扩展革命：支持更长推理链的技术（如增加生成长度）显示，有效的推理需要大量的推理时计算空间。这为模型提供了一个“认知工作区”，使其能够系统地展开和应用其预训练知识。
基于这两点，本文假设，只要模型具备了丰富的预训练知识和足够的推理时计算空间，激活其推理能力可能仅需少量高质量的训练样本，而非大规模微调。
本文方法
本文方法的核心是基于“少即是多推理（LIMO）”假说，通过构建一个极小但高质量的数据集来高效地激发预训练模型的复杂推理能力。
LIMO假说
LIMO假说的核心思想是：对于一个在预训练阶段已经学到充分领域知识的基础模型，其复杂的推理能力可以通过少量、但经过精心设计的认知过程演示来有效激活。成功的激发依赖于两个前提：
- 模型参数空间中潜藏着必要的先验知识。
- 存在高质量的推理链，能将复杂问题精确分解为详尽、符合逻辑的步骤，使认知过程清晰可追溯。
LIMO数据集构建
为了验证该假说，本文构建了一个高质量的小规模数据集 $\mathcal{D} = {(q_i, r_i, a_i)}_{i=1}^{N}$，其中 $q$ 是问题，$r$ 是推理链，$a$ 是答案，$N$ 被有意保持得很小（817个）。
问题选择
高质量的问题应能自然地引出长推理过程。选择标准如下：
- 高难度：优先选择能促进复杂推理链、多样化思维过程和知识整合的挑战性问题。
- 通用性/分布外：选择偏离模型训练分布的问题，以挑战其固化思维，鼓励探索新的推理路径。
- 知识多样性：问题应覆盖多个数学领域，要求模型在解题时整合和连接不同知识点。
为此，本文从NuminaMath、AIME、MATH等多个数据集中筛选问题。筛选过程采用多阶段过滤：首先用中等能力的模型（Qwen2.5-Math-7B-Instruct）筛掉简单问题；然后用SOTA模型（如R1）进一步过滤，仅保留那些即使是顶级模型成功率也很低的问题；最后通过策略性采样确保问题覆盖范围和多样性，最终从数千万问题中精选出817个。
推理链构建
高质量的解题过程（推理链）对于模型学习至关重要。本文通过收集官方答案、人类专家和AI专家的解法，并利用SOTA模型生成多种解题思路，再通过自我蒸馏技术扩充候选解。通过对这些候选解的分析，总结出高质量推理链的三个关键特征：
- 最优的结构组织：解题步骤结构清晰，详略得当。在关键推理节点上使用更多篇幅进行详细阐述，而对简单步骤则保持简洁。这种自适应的粒度确保了复杂逻辑得到充分解释。
- 有效的认知脚手架：解题过程提供策略性的引导，逐步构建理解。例如，渐进式地引入概念，在关键点明确阐述洞见，填补概念鸿沟，使复杂推理过程更易学习。
- 严谨的验证：在整个推理过程中频繁地包含验证步骤，如检查中间结果、核对假设、确认每一步推导的逻辑一致性，从而确保最终答案的可靠性。
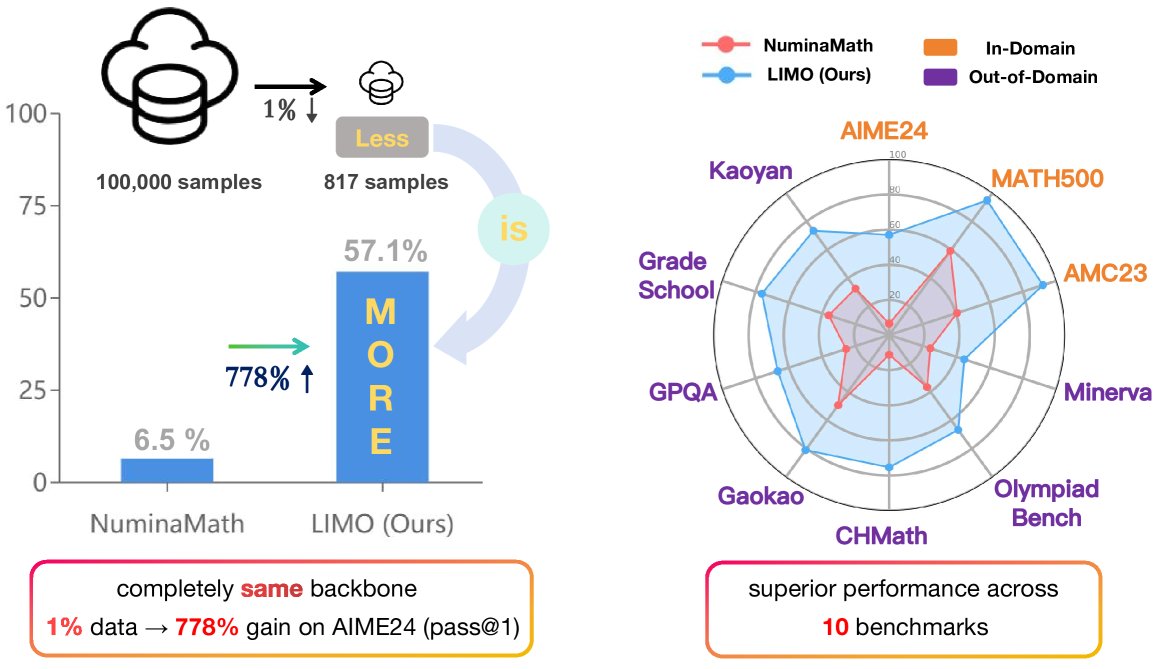图1：LIMO用更少的样本在多个数学和跨学科基准上取得了显著优于NuminaMath的性能。
基于以上标准，本文采用规则过滤和LLM辅助相结合的方法，为每个选定的问题匹配最高质量的推理链，最终构成了LIMO数据集。
训练与评估
- 训练协议：使用LIMO数据集对Qwen2.5-32B-Instruct模型进行全参数监督微调（SFT）。
- 评估框架：
- 域内评估：在AIME24、MATH500和AMC23等知名数学竞赛基准上进行测试。
- 域外（OOD）评估：在更多样化的基准上测试泛化能力，包括：
- 不同数学竞赛：OlympiadBench。
- 新颖的多语言基准：使用2024年最新的中文考试题构建CHMath（中国高中数学联赛）、Gaokao（高考）、Kaoyan（考研）等，以测试跨语言推理能力。
- 跨学科基准：Minerva（本科STEM问题）和GPQA（多学科问题），测试推理能力向更广泛领域的迁移。
实验结论
实验结果表明，LIMO在域内和域外任务上均表现出卓越的性能和数据效率。
主要结果
如下表所示，LIMO在所有基准测试中的平均性能（72.8%）最高，显著优于包括OpenAI-o1-preview（61.1%）在内的所有基准模型。尤其值得注意的是，LIMO仅使用了817个训练样本，而其他SFT模型（OpenThoughts和NuminaMath）使用了超过10万个样本，但性能远不及LIMO。
- 域内性能：在AIME24上达到57.1%的准确率，在MATH500上达到94.8%，在AMC23上达到92.0%，均大幅领先于SOTA模型。
- 域外泛化：在OlympiadBench（66.8%）、CHMath（75.4%）和Gaokao（81.0%）等OOD基准上也表现出强大的泛化能力，显著优于基座模型和其他对比模型。
| 数据集 | OpenAI-o1 -preview | Qwen2.5-32B -Instruct (基座) | QwQ-32B- preview | OpenThoughts (114k) | NuminaMath (100k) | LIMO (本文, 817) |
|---|---|---|---|---|---|---|
| 域内 | ||||||
| AIME24 | 44.6 | 16.5 | 50.0 | 50.2 | 6.5 | 57.1 |
| MATH500 | 85.5 | 79.4 | 89.8 | 80.6 | 59.2 | 94.8 |
| AMC23 | 81.8 | 64.0 | 83.6 | 80.5 | 40.6 | 92.0 |
| 域外 | ||||||
| OlympiadBench | 52.1 | 45.3 | 58.5 | 56.3 | 36.7 | 66.8 |
| CHMath | 50.0 | 27.3 | 68.5 | 74.1 | 11.2 | 75.4 |
| Gaokao | 62.1 | 72.1 | 80.1 | 63.2 | 49.4 | 81.0 |
| Kaoyan | 51.5 | 48.2 | 70.3 | 54.7 | 32.7 | 73.4 |
| GradeSchool | 62.8 | 56.7 | 63.8 | 39.0 | 36.2 | 76.2 |
| Minerva | 47.1 | 41.2 | 39.0 | 41.1 | 24.6 | 44.9 |
| GPQA | 73.3 | 48.0 | 65.1 | 42.9 | 25.8 | 66.7 |
| 平均 | 61.1 | 49.9 | 66.9 | 58.3 | 32.3 | 72.8 |
表3: 模型在各类数学推理基准上的性能对比 (pass@1)。LIMO（蓝色高亮）尽管使用的训练样本（817）远少于其他微调模型（>100k），但性能最优。
影响因素分析
推理链质量的影响
为了验证推理链质量的关键作用，本文将500个问题的解法按质量分为5个等级（L1最低，L5最高），并分别用它们来训练模型。结果如下图所示，使用L5质量推理链训练的模型性能最佳，而质量越低，性能越差。这证明了高质量的推理链（结构清晰、解释详尽、自我验证）是激发模型能力的核心。
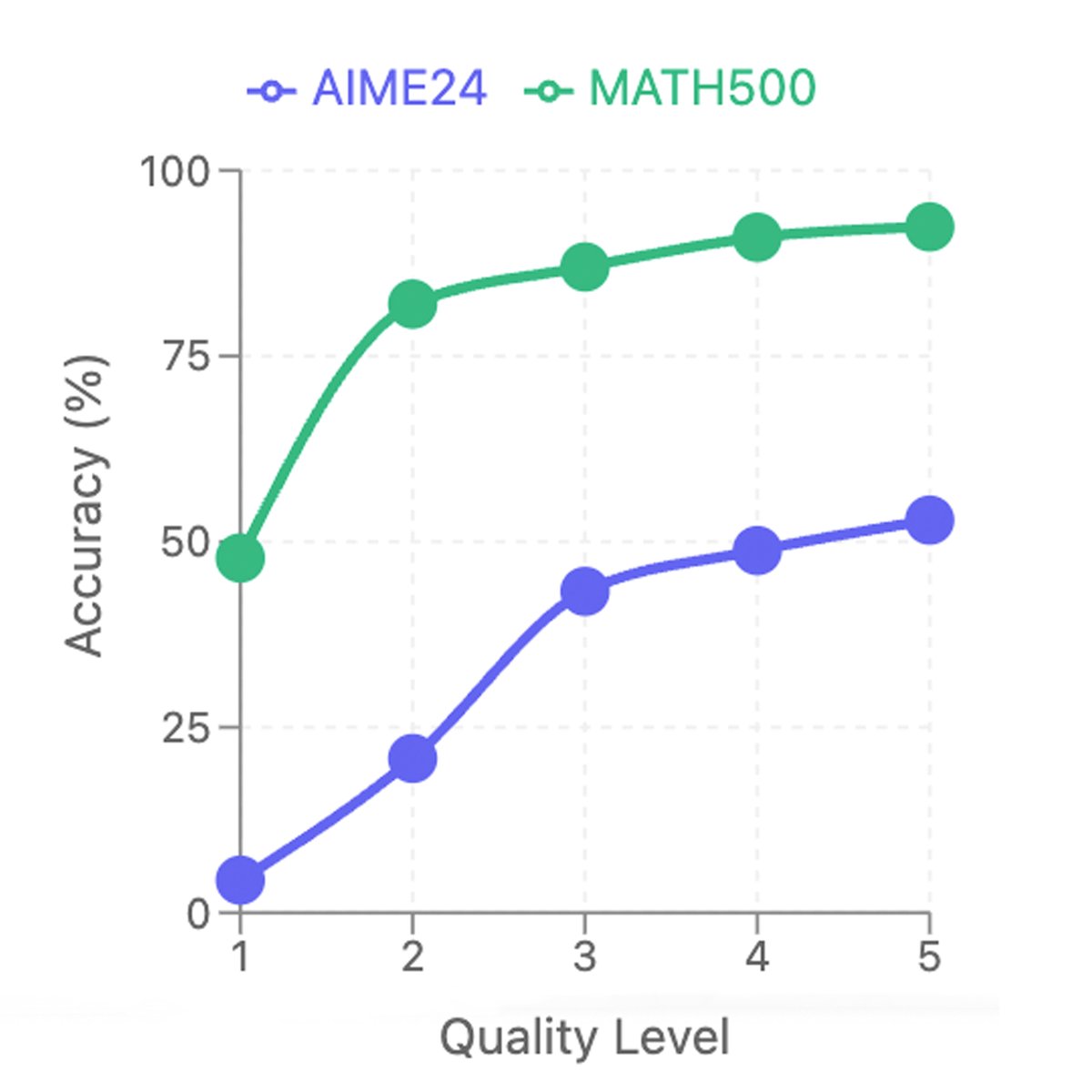图2: 模型在不同质量等级的推理链上训练后的性能对比。
问题质量的影响
为了探究问题难度对模型推理能力的影响，本文分别使用“简单”、“复杂”和“高级”三个不同难度级别的问题集（各500个）进行训练。结果显示，用更难的问题（Advanced-500）训练的模型，在AIME2024和MATH500上的表现均优于用简单问题训练的模型，证明了训练数据中的问题挑战性越高，越能激发模型的泛化推理能力。
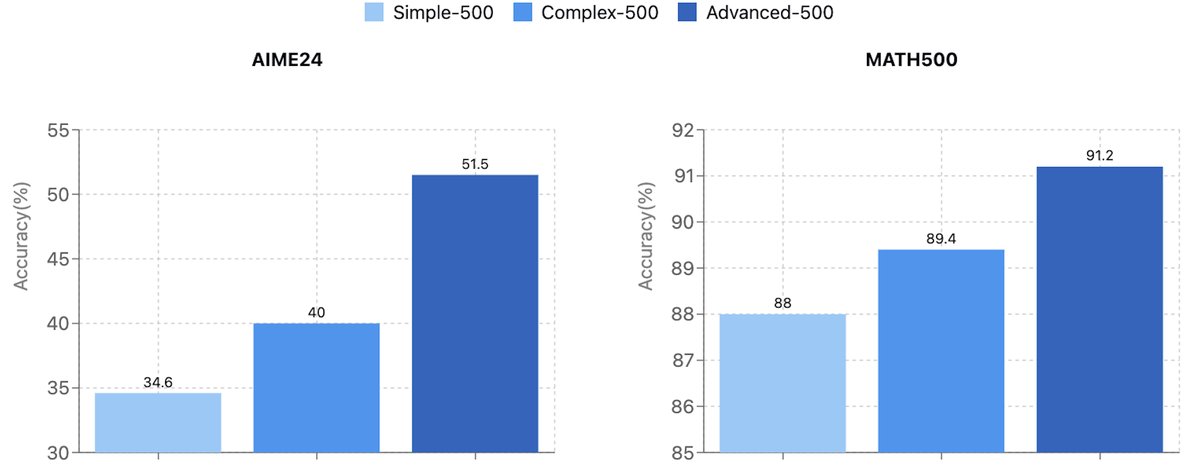图3: 在不同质量问题上训练的模型在MATH和AIME基准上的性能对比。
LLM基座的影响
为了验证LIMO假说中“预训练知识是前提”的观点，本文在两个不同版本的Qwen 32B模型（Qwen1.5和Qwen2.5）上进行了相同的LIMO微调。结果显示，在数学预训练上更强的Qwen2.5基座上，LIMO的效果远超在Qwen1.5上的表现（AIME准确率57.1% vs 10.0%）。这表明，更强的预训练知识基础使得模型能更有效地利用LIMO提供的高质量示例。
图4: 预训练模型选择对数学推理性能的影响。
案例分析
定性分析显示，LIMO模型学会了类似DeepSeek-R1的复杂行为，如进行长链条思考和自我反思/验证（例如，会说出“等等，让我再检查一遍”）。而基座模型则缺乏这种能力。定量分析也发现，由更高质量数据训练出的模型，其生成的回应更长，并更多地使用“等等”、“也许”、“因此”这类表示思考和过渡的词语。
图5: Qwen2.5-32B-Instruct（基座模型）、DeepSeek-R1和LIMO的回答对比。
总结
实验结果强有力地支持了LIMO假说。复杂的推理能力并非一定要通过海量数据“教会”，而是可以在一个知识丰富的模型中被高效“激发”。数据质量（包括问题的挑战性和推理链的认知深度）远比数量更重要，这为未来高效开发AGI的复杂能力指明了一个有前景的技术路径。