LLM-guided Hierarchical Retrieval
-
ArXiv URL: http://arxiv.org/abs/2510.13217v1
-
作者: Nilesh Gupta; Inderjit S. Dhillon; Wei-Cheng Chang; Cho-Jui Hsieh
-
发布机构: Google; UCLA; University of Texas at Austin
TL;DR
本文提出了一种名为 LATTICE 的LLM引导分层检索框架,通过将海量文档组织成语义树,并让大型语言模型(LLM)基于创新的校准路径相关性得分进行推理和导航,从而以对数级的搜索复杂度高效解决复杂的推理密集型查询。
关键定义
本文提出或沿用了以下对理解其方法至关重要的核心概念:
- LLM引导的分层检索 (LLM-guided Hierarchical Retrieval):本文提出的核心框架。它将信息检索任务分为两个阶段:离线构建语料库的语义树,以及在线由一个“搜索LLM”导航该树以找到相关文档。
- 语义树 (Semantic Tree):一种对文档语料库进行组织的树状结构。叶节点代表原始文档,而内部节点则是由LLM生成的、对其子节点内容的文本摘要。这种结构为LLM的导航提供了语义上的脚手架。
- 本地评分器 (Local Scorer, $\mathcal{L}$):对“搜索LLM”功能的一种抽象。它接收一个查询 \(q\) 和一个候选节点列表,并为每个节点输出一个表示局部相关性的分数 \(s\)。这些分数是上下文相关的,并且存在噪声。
- 潜在分数 (Latent Score, $\hat{s}_{v}$):为了解决LLM评分的噪声和上下文依赖性问题,本文引入的一个核心概念。它是一个与评估列表(slate)无关的、潜在的真实相关性分数。该分数通过对所有历史局部评分进行最大似然估计(MLE)来计算,从而校准LLM的原始输出。
- 路径相关性分数 (Path Relevance Score, $\hat{p}_{rel}(v)$):用于在整个树中进行全局比较和引导搜索的关键指标。它通过一个指数移动平均公式,结合了从根节点到当前节点 \(v\) 的路径上所有节点的校准后潜在分数,公式为 \($\hat{p}\_{rel}(v)=\alpha \cdot \hat{p}\_{rel}(\text{parent}(v))+(1-\alpha) \cdot \hat{s}\_{v}\)$。
相关工作
当前基于LLM的信息检索(IR)领域主要存在以下范式及其瓶颈:
- 检索-重排 (Retrieve-then-Rerank):这是目前主流的范式。它首先使用一个低成本的检索器(如BM25或密集检索)召回大量候选文档,然后由一个强大的LLM进行重排序。其主要瓶颈在于,最终效果受限于初始检索阶段的质量。如果关键文档在第一阶段未能被召回,再完美的重排器也无能为力。此外,初始检索通常依赖于浅层语义,难以处理需要多步推理的复杂查询。
- 生成式检索 (Generative Retrieval, GenIR):
- 参数化方法:将语料库隐式存储在模型参数中。这类方法难以更新知识,且容易产生幻觉。
- 长上下文方法:将整个语料库放入LLM的上下文中。这种方法允许LLM在完整文本上进行推理,但由于自注意力机制的超线性计算复杂度,对于大规模语料库来说,其成本和延迟是无法接受的。
本文旨在解决的问题是:如何结合LLM强大的推理能力和分层结构的高效性,以克服现有范式的局限性。具体而言,本文旨在创建一个既能处理复杂推理查询,又具备高可扩展性和计算效率,同时还能方便地更新知识的新型检索框架。
本文方法
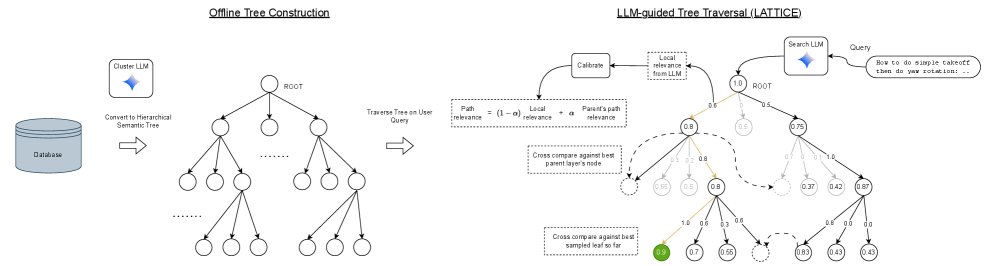
LATTICE框架概览。左侧为离线阶段,将非结构化语料库组织成语义树;右侧为在线阶段,搜索LLM通过最佳优先遍历和校准后的路径相关性分数来查找与查询相关的文档。
本文提出的 LATTICE 框架包含两个核心阶段:离线树构建和在线LLM引导的层次化搜索。
离线树构建
目标是创建一个树状结构 $T=(V,E)$,其中叶节点是文档,内部节点是摘要。本文探索了两种LLM驱动的构建策略:
1. 自下而上的聚类与摘要(Bottom-Up)
该方法从叶节点(文档)开始,逐层向上构建树:
- 初始层形成:将所有文档作为叶节点。通过聚类算法(如谱聚类)或利用文档元数据(例如,将同一来源的文章段落分组),将叶节点分组,形成第一层父节点。每组的节点数不超过预设的最大分支因子 $M$。
- 迭代循环:对上一层生成的每个节点(代表一个文档簇),使用LLM为其子节点内容生成一份文本摘要。然后,对这些新生成的摘要进行嵌入(embedding)和再次聚类,形成更高一层的父节点。
- 终止:重复上述“摘要-嵌入-聚类”的循环,直到当前层的节点数小于或等于 $M$。最后,将这些顶层节点连接到一个单一的根节点,完成树的构建。
2. 自上而下的划分式聚类(Top-Down)
该方法从根节点开始,递归地将整个语料库进行划分:
- 多级摘要预处理:由于在顶层划分时需要对文档有高度概括的理解,该方法首先为每个文档生成多个层次的摘要(从1-2个词的标签到更详细的段落)。
- 递归划分:从包含所有文档的根节点开始。在每一步,对于一个待划分的节点 \(v\),为其所有叶子后代选择一个合适的摘要级别。然后,将这些摘要提供给LLM,要求其将它们划分成最多 $M$ 个概念主题。
- 新节点创建:LLM返回每个主题的描述以及摘要到主题的映射。据此创建 $M$ 个新的内部节点,并将 \(v\) 的叶子后代根据映射关系重新分配给这些新节点。这些新节点成为 \(v\) 的子节点。任何子节点数仍超过 $M$ 的新节点将被加入队列,等待进一步划分。
- 终止:当队列为空时,划分过程结束。
在线LLM引导的层次化搜索
这是本文方法的核心创新,其目标是利用LLM的推理能力,在语义树上进行高效、准确的导航。

LATTICE在BRIGHT基准测试上的一个真实查询搜索过程。节点颜色代表其路径相关性;黄色高亮路径指向真实答案文档。搜索LLM在每个内部节点逐步决策,决定下一步探索哪个分支。
该搜索算法(见下表)是一个带有束搜索(beam search)的最佳优先遍历过程,其关键在于如何处理LLM评分的噪声和不一致性。
| 算法:LLM引导的层次化搜索 |
|---|
| 输入: 查询 $q$, 树 $T$, 评分LLM $\mathcal{L}$, 束大小 $B$, 迭代次数 $N$, Top-K $K$, 动量 $\alpha$ |
| 1. 初始化: |
| - 创建最大优先队列 \(Frontier\) $F$ 和预测集 \(Pred\) $\leftarrow\emptyset$ |
| - 初始化评分历史 \(ScoreHistory\) 和潜在分数 \(LatentScores\) |
| - $\hat{p}_{rel}(v_{root})\leftarrow 1.0$, 将根节点加入$F$ |
| 2. 迭代搜索 (for $i=1$ to $N$): |
| - 从 $F$ 中取出路径相关性最高的 $B$ 个节点作为 \(Beam\) |
| - For each $v$ in \(Beam\): |
| - 评估列表构建: \(Slate\) $\leftarrow C(v)+Aug(v)$ (Aug(v) 是用于校准的增强节点) |
| - 局部评分: \(LocalScores\) $\leftarrow\mathcal{L}(q, \text{Slate})$ |
| - 将新评分加入 \(ScoreHistory\) |
| - 潜在分数估计: $\text{LatentScores}\leftarrow\text{SolveMLE}(\text{ScoreHistory})$ |
| - for each $v^{\prime}$ in \(Slate\): |
| - 更新 $\hat{s}_{v^{\prime}}$ 并计算路径相关性 $\hat{p}_{rel}(v^{\prime}) \leftarrow \alpha \cdot \hat{p}_{rel}(\text{parent}(v^{\prime}))+(1-\alpha) \cdot \hat{s}_{v^{\prime}}$ |
| - for each $v^{\prime}$ in $C(v)$: |
| - if $v^{\prime}$ 是叶节点, 加入 \(Pred\) |
| - else, 加入 $F$ |
| 3. 返回: 从 \(Pred\) 中按 $\hat{p}_{rel}$ 排序的Top-K个节点 |
创新点
- 带有校准的评估列表构建 (Slate Construction with Calibration):为了让LLM的评分更稳定,每次评估一个节点的子节点时,评估列表(slate)中会加入一些“锚点”节点。
- 内部节点评估:加入当前节点的得分最高的兄弟节点,以提供跨分支的比较基准。
- 叶节点评估:加入从当前已发现的最佳叶节点中采样的几个节点,这有助于将新叶子的评分锚定在已知的最佳候选项上。
- 潜在分数估计与路径相关性更新 (Latent Score Estimation and Path Relevance Update):这是解决LLM评分不一致性的关键。
- 本文假设LLM观察到的分数 $s^{i}_{v}$ 是一个潜在真实分数 $\hat{s}_{v}$ 经过线性变换 $s^{i}_{v}\approx a\cdot\hat{s}_{v}+b^{i}$ 后的结果,其中 $a$ 是全局缩放因子,$b^{i}$ 是每次评估的偏置。
-
通过求解一个最小化均方误差(MSE)的最大似然估计(MLE)问题,从所有历史评分中联合估计出所有节点的潜在分数 ${\hat{s}_{v}}$ 以及变换参数。
\[\min\_{a,\{\hat{s}\_{v}\},\{b^{i}\}}\sum\_{i}\sum\_{v\in\text{slate}^{i}}(s^{i}\_{v}-(a\cdot\hat{s}\_{v}+b^{i}))^{2}.\] - 这个校准后的潜在分数 $\hat{s}_{v}$ 被用来更新全局可比的 路径相关性分数 $\hat{p}_{rel}(v)$,该分数综合了从根到当前节点的整条路径上的信息,以指导搜索向最有希望的方向进行。
实验结论
实验在专为评估深度推理能力设计的 BRIGHT 基准上进行。LATTICE 方法在严格的零样本(zero-shot)设置下进行评估,即不针对 BRIGHT 任务进行任何微调。
| 方法 | 生物 | 食物 | 经济 | 历史 | 物理 | 心理 | 机器人 | LeetCode | AoPS | TheoremQ | A. Math | T. Math | 平均 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DivIR | 68.2 | 80.5 | 69.4 | 69.8 | 69.4 | 62.7 | 62.9 | 63.8 | 64.9 | 60.1 | 55.4 | 55.2 | 65.2 |
| DIVER-v2 | 78.2 | 82.2 | 77.2 | 72.4 | 74.0 | 72.8 | 67.9 | 73.5 | 78.1 | 68.2 | 70.6 | 67.0 | 73.5 |
| ReasonIR | 65.2 | 74.9 | 69.8 | 66.8 | 70.8 | 67.5 | 63.1 | 58.7 | 63.7 | 56.4 | 55.9 | 50.8 | 63.6 |
| XRR2 | 70.6 | 77.4 | 67.0 | 72.6 | 71.0 | 66.1 | 63.3 | 64.3 | 64.7 | 61.2 | 58.1 | 54.4 | 65.9 |
| LATTICE (本文) | 77.1 | 82.3 | 78.9 | 68.3 | 74.1 | 75.3 | 76.0 | 49.3* | 60.6* | 52.8* | 59.9* | 51.1* | 70.5 |
各方法在BRIGHT基准上的nDCG@10性能。粗体表示最佳,下划线表示零样本方法中的最佳,*表示数据集使用动态语料库。
优点
- 顶尖的零样本性能:在BRIGHT基准测试中,LATTICE 展现了最先进的零样本性能。在采用静态语料库的7个StackExchange子集上,其平均 nDCG@10 达到 76.0%,显著优于同样使用Gemini-2.5-flash进行重排的强基线(69.3%)。与次优的零样本基线相比,Recall@100 提升高达 9%,nDCG@10 提升高达 5%。
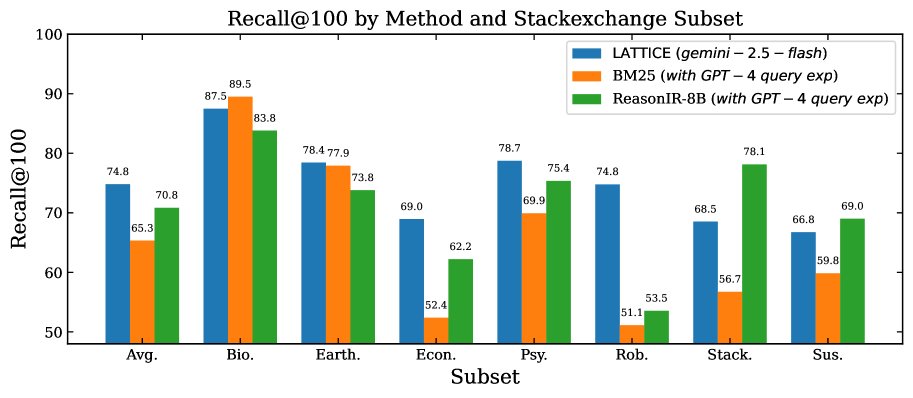
LATTICE在StackExchange子集上的Recall@100表现优于BM25和微调过的ReasonIR-8B。
-
与微调SOTA方法媲美:在静态语料库子集上,LATTICE 的零样本性能与为BRIGHT基准特别微调的SOTA方法 DIVER-v2 具有高度竞争力,甚至在经济学和机器人学等领域取得了最佳结果。
-
更高的计算效率:成本-性能分析表明,LATTICE 的可扩展性优于“检索-重排”基线。随着LLM处理的Token数量增加(即搜索更深),重排基线的性能迅速饱和,而 LATTICE 的 nDCG@10 持续提升,证明了LLM引导的层次化遍历在计算上更高效。
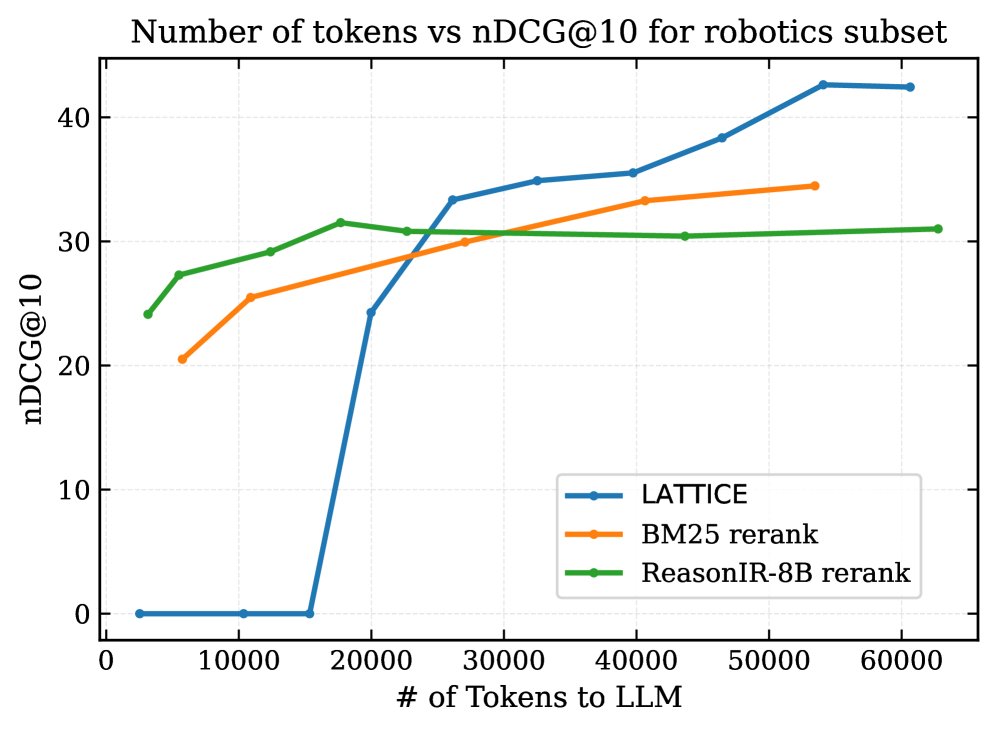
在Robotics子集上,LATTICE(蓝色)与重排基线相比,随着LLM计算成本增加,性能能够扩展到更高水平。
缺点/局限性
- 在动态语料库上表现不佳:在LeetCode等使用“查询依赖的动态语料库”的任务上,LATTICE 性能显著低于基线。这是因为基准测试会为每个查询动态排除一部分文档,而LATTICE离线构建的树无法实时更新父节点的摘要内容,导致这些过时的摘要错误地引导了搜索。相比之下,“检索-重排”方法可以简单地在后处理中过滤掉这些文档。值得注意的是,大多数真实世界的IR系统都运行在静态或缓慢变化的语料库上,该问题属于基准测试的特定设计。
总结
本文提出的 LATTICE 框架成功地将LLM的推理能力与分层搜索的效率相结合,创建了一种新颖、强大且高效的检索范式。实验结果证明,通过让LLM直接在语义树上进行智能导航,并辅以创新的分数校准机制,该方法在复杂的推理式检索任务上取得了顶尖的零样本性能,为未来LLM在IR领域的深度应用开辟了新的道路。