LLMs Encode How Difficult Problems Are

ArXiv URL: http://arxiv.org/abs/2510.18147v1
作者: Chris Russell
发布机构: University of Oxford

TL;DR

本文通过一系列实验发现，大型语言模型（LLMs）的内部激活向量中，确实以线性的方式编码了问题的难度，但这种编码与人类判断的对齐程度远高于与其它LLM性能评估的对齐程度；并且，在强化学习训练过程中，与人类判断一致的难度表征会得到加强，而与LLM性能相关的难度表征则会退化。

关键定义

本文主要沿用并验证了领域内已有的关键定义，并将其应用于难度表征的研究中，核心概念包括：

线性探针 (Linear Probes): 一种简单的线性模型，用于训练在从LLM特定层和Token位置提取的激活（activations）上，以预测某个“基准真实”标签（如问题难度）。本文使用它来验证难度信息是否线性存在于模型的表征空间中。
难度表征 (Difficulty Representation): 本文的核心假设，即问题的难易程度在LLM的激活空间中作为一个可被解码的、线性的方向或轴存在。本文区分了两种难度的来源：人类标注的难度和基于LLM性能评估的难度。
引导/操控 (Steering): 在模型推理生成过程中，通过向模型的激活向量中添加一个特定方向的向量（此处是由线性探针学习到的“从易到难”的难度向量），从而“引导”模型的生成行为，以观察其对模型性能和输出风格的影响。
基于可验证奖励的强化学习 (Reinforcement Learning from Verifiable Rewards, RLVR): 一种强化学习后训练方法，用于增强模型的推理能力。它使用基于规则的结果（如数学题的最终答案是否正确）作为奖励信号来优化模型。本文使用此方法来追踪难度表征在模型能力提升过程中的演变。

本文方法

本文设计了一套系统的实验流程，通过线性探测、表征引导和追踪强化学习过程，来研究LLM内部的难度表征。

难度探测实验

数据与模型：实验使用了Easy2Hard-Bench中的两个数学子集：E2H-AMC（难度基于人类竞赛者的表现）和E2H-GSM8K（难度基于其他LLMs的表现）。研究涵盖了来自5个主要系列（Qwen, LLaMA, DeepSeek等）的60个不同大小和专长的模型变体。
探测方法：对每个问题，在模型生成答案的每个Token位置，提取所有层的激活（内部隐藏状态）。然后，训练一个线性回归探针，用这些激活来预测问题的真实难度分数（一个连续值）。
评估：使用5折交叉验证，并以预测难度与真实难度之间的斯皮尔曼秩相关系数（Spearman rank correlation, $\rho$）作为探针性能的度量。同时，通过拟合一个幂律公式来分析探针性能随模型参数量（N）变化的伸缩法则（scaling law）：
\[1-\text{$\widehat{\rho}\_{\ell,p}^{\mathrm{CV}}$}=C\cdot N^{-\alpha}\]
其中 $\alpha > 0$ 表示性能随模型增大而提升。

沿难度轴进行引导

基于难度探测实验中发现的“从易到难”的线性方向（即探针的权重向量），本文进行了引导实验。在推理时，将该向量乘以一个引导系数 $\alpha$ (ranging from -3 to +3) 后，加到模型的激活中。负系数 $\alpha < 0$ 表示朝“更容易”的方向引导，正系数 $\alpha > 0$ 表示朝“更难”的方向引导。通过观察模型在MATH500基准测试上的Pass@1准确率，来评估引导的效果。

在GRPO训练中追踪难度表征

为了探究难度表征如何随模型能力一同演变，本文对Qwen2.5-Math-1.5B模型进行了GRPO（一种策略梯度RL算法）训练。

训练设置：使用MATH训练集，并筛选出难度大于等于3的问题进行训练。在训练过程的每一步都保存模型检查点。
追踪与评估：对每个模型检查点，重复上述的难度探测实验，分别训练针对人类难度（E2H-AMC）和LLM难度（E2H-GSM8K）的探针。同时，在MATH500测试集上评估每个检查点的Pass@1准确率。通过这种方式，可以并行追踪模型任务性能和其内部难度表征强度的变化。

实验结论

人类判断的难度在LLM激活中被清晰地线性编码

数据集	最佳 $\widehat{\rho}_{\ell,p}^{\mathrm{CV}}$	模型（层，位置）
E2H-AMC	0.8799	Llama-3.1-32B-R1 (61, -2)
	0.8780	Llama-3.1-32B-R1 (74, -1)
E2H-Codeforces	0.7980	Llama-3.1-32B-Base (41, -1)
	0.7571	Llama-3.1-8B-Base (16, -1)
E2H-GSM8K	0.5639	Llama-3.1-32B-R1 (38, -3)
	0.5516	Llama-3.1-32B-R1 (15, -5)

如上表所示，探测人类难度（E2H-AMC）的探针性能非常高（$\rho \approx 0.88$），而探测LLM难度（E2H-GSM8K）的探针性能则差很多（$\rho \approx 0.58$）。这表明模型内部表征与人类感知的难度高度对齐，但与LLM自身性能评估的难度关联较弱。

难度表征随模型尺寸扩展，但存在差异

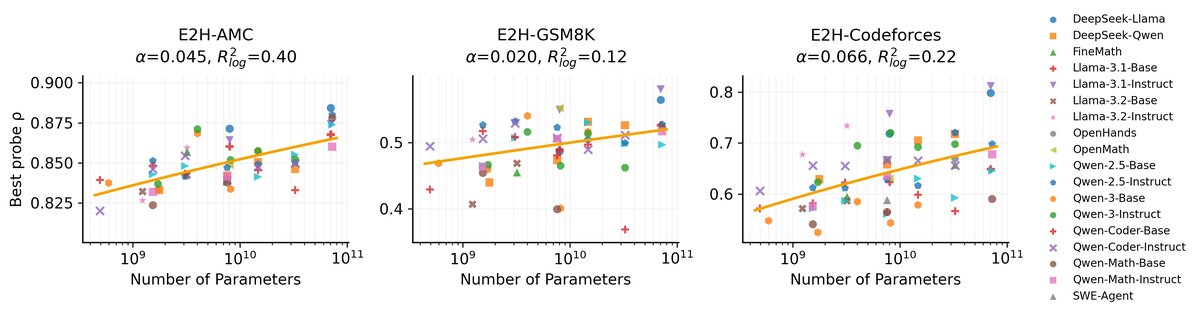
The scatterplot shows the best performing probes for various models on each of the three chosen datasets.

探针性能与模型大小存在幂律关系。如图所示，基于人类标签的数据集（E2H-AMC和E2H-Codeforces）表现出更强、更清晰的伸缩趋势（$\alpha=0.045$ 和 $\alpha=0.066$），而基于LLM标签的GSM8K伸缩趋势最弱（$\alpha=0.020$）。这进一步证明了人类难度信号在不同模型中更具鲁棒性。

最佳探测位置因任务领域而异

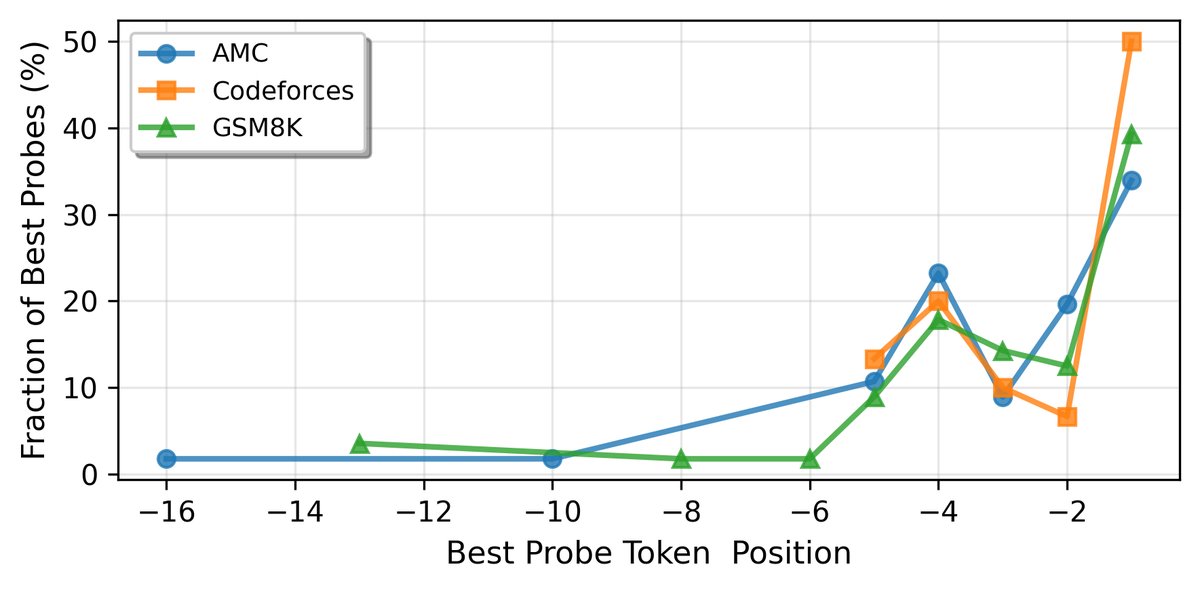
Percentage of best-performing probes at each token position.

对于代码任务（Codeforces），50%的最佳探针出现在提示的最后一个Token位置。而对于数学任务（AMC, GSM8K），最佳探针位置分布在最后几个Tokens上，不完全集中在最后一个。这表明不同任务的难度信号在模型处理输入的不同阶段被编码。

引导模型表征可改善性能

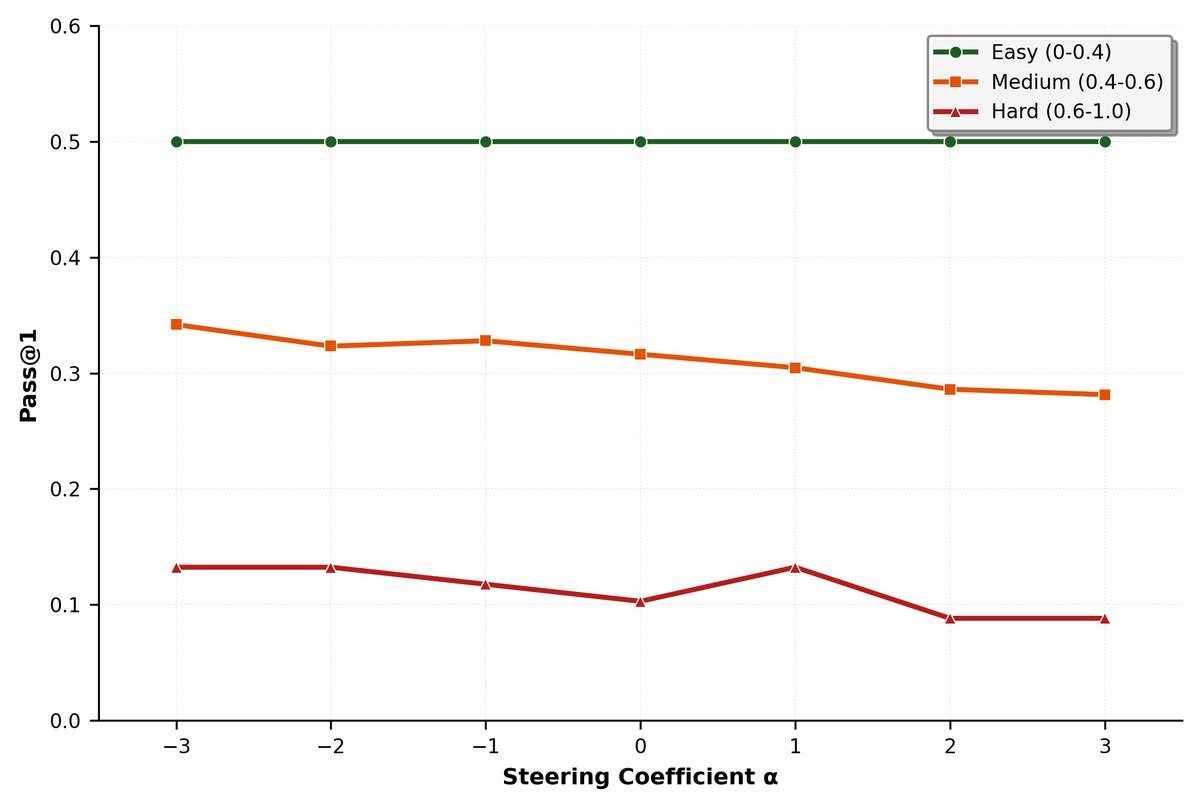
Pass@1 accuracy on MATH500 for Qwen2.5-Math-1.5B across steering coefficients.

在Qwen2.5-Math-1.5B模型上，沿“更容易”的方向引导（$\alpha < 0$）显著提高了在MATH500上的准确率。例如，在 $\alpha=-3$ 时，模型倾向于生成更简洁、使用代码工具辅助的推理路径，从而减少了幻觉并得到正确答案。相反，向“更难”方向引导（$\alpha > 0$）则降低了准确率。

领域专门化的后训练对难度表征的影响好坏参半

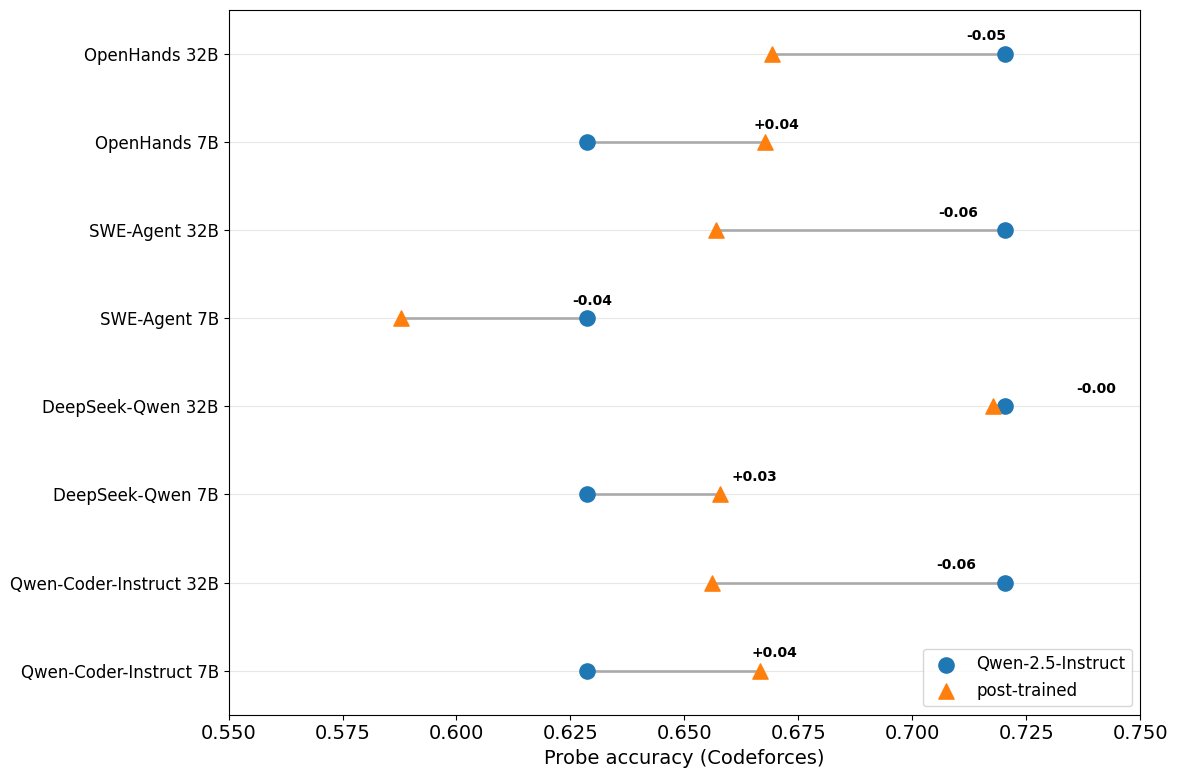
Probe accuracy on Codeforces for Qwen-2.5-Instruct and its specialised variants.

与基础指令微调模型相比，额外的任务专属微调（如为代码任务优化的模型）对难度表征的影响不一。对于7B参数的模型，专属微调有轻微提升；但对于32B参数的模型，反而有轻微的性能下降。这表明指令微调本身已足以形成稳固的难度表征，尤其是在大模型中。

GRPO训练过程中的难度表征演变

模型	Baseline Pass@1	Peak Pass@1	Peak Step
Qwen2.5–Math–1.5B (本文)	64.7	76.9	43/67

Oat–Zero–1.5B (Dr.GRPO 报告)	61.8	74.2	NA/11,200

本文的GRPO训练成功提升了模型的数学性能。在训练过程中：

Qwen2.5-Math-1.5B linear Probe performance across layers and training steps for the last three token positions.

人类难度表征得到加强：如图中上半部分（AMC probes）所示，随着训练步骤的增加，探测人类难度的探针性能保持稳定甚至有所提升。
LLM难度表征发生退化：如图中下半部分（GSM8K probes）所示，探测LLM难度的探针性能在模型的早、中层普遍下降，说明GRPO训练过程会系统性地“覆写”掉这个不稳定的信号。

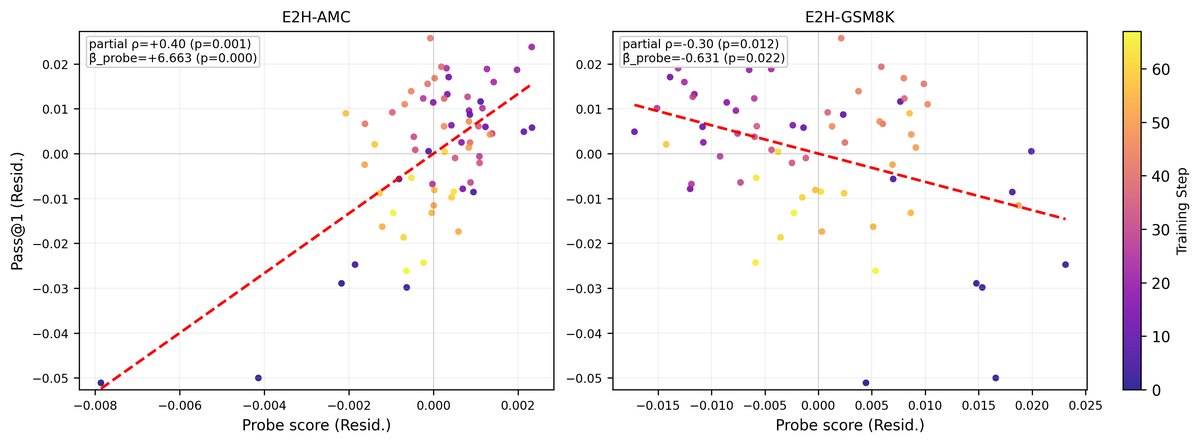
Each point represents a training checkpoint for Qwen2.5-Math-1.5B.

在排除了训练步数的影响后，探针性能与模型测试准确率之间的关系更加清晰：

人类难度探针的性能与模型性能呈强正相关（$\beta$=+6.66），说明更强的难度表征伴随着更高的数学能力。
LLM难度探针的性能与模型性能呈负相关（$\beta$=-0.63），说明随着模型变强，其内部对LLM难度的表征反而变弱了。

总结

本文的发现揭示了一个关键的不对称性：LLMs能够很好地隐式表征人类感知的难度，但却无法在显式生成或表征其他LLM的难度时做到这一点。通过操控这一内部表征可以切实地改善模型性能。更重要的是，在通过强化学习提升能力时，模型会自发地加强与人类判断一致的难度表征，同时削弱与LLM性能相关的、不稳定的难度信号。这表明，一个精确、稳定的内部难度感知可能是发展高级推理能力（如数学）的功能性组成部分。