MeSH: Memory-as-State-Highways for Recursive Transformers

• ArXiv URL: http://arxiv.org/abs/2510.07739v1

• 作者: Yizhen Zhang; Yadao Wang; Wenbo Su; Rujiao Long; Xiaobo Shu; Yuchi Xu; Haoyi Wu; Chengting Yu; Ziheng Chen; Bo Zheng; 等11人

• 发布机构: Alibaba; ShanghaiTech University; Zhejiang University

---

TL;DR

• 本文提出了一种名为 MeSH (Memory-as-State-Highways) 的新架构，通过引入一个由动态路由器管理的外部存储缓冲区，解决了朴素递归 Transformer 中的计算瓶颈和信息过载问题，从而显著提升了模型的性能和参数效率。

关键定义

本文为解决递归 Transformer 的性能瓶颈，提出了以下关键概念：

• 无差别计算 (Undifferentiated computation): 指在朴素递归模型中，由于缺乏关于当前迭代步骤的位置信息，权重共享的核心模块在每一次迭代中都被迫执行相似的计算模式。这导致了计算资源的利用效率低下，具体表现为“计算偏斜”（大部分计算集中在首次迭代）和“表示停滞”（模型陷入不动点，无法有效优化表示）。

• 信息过载 (Information overload): 指在递归结构中，单一的隐藏状态向量需要同时承担多种冲突的角色：保存长期信息以防遗忘、为下一次迭代准备中间特征、以及为最终预测层提供即时特征。这种多重负担迫使模型学习一个低维的“折衷”表示，导致“维度坍缩”，即表示的有效维度和表达能力显著下降。

• MeSH (Memory-as-State-Highways): 本文提出的核心架构。它通过将状态管理外部化到一个显式的多槽存储缓冲区（State Buffer）来解决上述问题。该缓冲区由一系列与迭代步骤相关的、可学习的轻量级读写路由器（Routers）控制，从而将隐式的状态管理挑战转化为一个清晰、可学习的路由问题，实现了持久化记忆与瞬时计算的分离。

相关工作

当前，为了应对大模型参数扩展的瓶颈，递归 Transformer (Recursive transformers) 作为一个参数高效的架构受到了越来越多的关注。其核心思想是通过循环复用一个权重共享的核心计算块，来解耦模型的计算深度与参数深度。这使得模型能够根据任务难度动态分配计算资源，并开辟了计算深度这一新的缩放维度。

然而，现有递归模型存在一个关键问题：在计算量相当的情况下，参数较少的递归模型性能往往落后于其非递归的对应版本。本文旨在深入探究并解决这一性能差距背后的根本原因。具体而言，本文诊断出两个主要瓶颈：

1. 无差别计算 (Undifferentiated computation)：模型无法区分迭代步骤，导致计算模式僵化，效率低下。
2. 信息过载 (Information overload)：单一的隐藏状态难以同时承载记忆、中间计算和输出等多重功能，导致表示能力受损。

尽管一些现有的启发式方法（如残差连接或锚定连接）试图通过固定的加性连接来缓解信息过载，但它们无法解决无差别计算的问题，并且缺乏适应性。

本文方法

为了系统性地解决朴素递归的内在缺陷，本文提出了 MeSH (Memory-as-State-Highways) 框架。

递归 Transformer 架构

本文采用 Prelude-Recurrent-Coda 结构。该结构包括：

• Prelude 网络 ($f_{\text{pre}}$): 处理初始 token 嵌入 $\mathbf{h}_{\text{emb}}$，生成循环的初始状态 $\mathbf{h}^{(0)}$。
• 核心循环: 将一个权重共享的核心模块 $f_{\text{core}}(\cdot)$ 重复应用 $K$ 次，从 $\mathbf{h}^{(0)}$ 迭代至 $\mathbf{h}^{(K)}$。
• Coda 网络 ($f_{\text{coda}}$): 处理最终的循环状态 $\mathbf{h}^{(K)}$，生成模型的最终表示 $\mathbf{h}_{\text{final}}$。

传统的启发式方法通过固定的加性连接来增强信息流，如残差连接（\(+residual\)）或锚定连接（\(+anchor\)），其通用更新规则为：

\[\mathbf{h}^{(t+1)}=f_{\text{core}}(\mathbf{h}^{(t)})+\mathbf{h}_{\text{sup}}^{(t)}\]

其中 $\mathbf{h}_{\text{sup}}^{(t)}$ 是补充上下文，如前一状态 $\mathbf{h}^{(t)}$ 或初始状态 $\mathbf{h}^{(0)}$。这些方法虽能部分缓解信息过载，但方案僵化，且无法解决无差别计算问题。

创新点：MeSH 架构

MeSH 框架用一个由动态路由器控制的外部存储器取代了简单的状态传递机制，从而实现了持久化记忆与瞬时计算的解耦。其核心组件如下：

1. 状态缓冲区 (State Buffer): MeSH 维护一个拥有 $B$ 个槽位的存储缓冲区 $\mathbf{M}={\mathbf{m}_{0},\ldots,\mathbf{m}_{B-1}}$。在循环开始前，第一个槽位 $\mathbf{m}_0$ 用初始 token 嵌入 $\mathbf{h}_{\text{emb}}$ 进行初始化，作为输入的持久锚点，其余槽位初始化为零。

2. 动态路由器 (Dynamic Routers): 每一轮迭代 $t$ 都配有独立的、可学习的写入路由器 $R_{\text{write}}^{(t)}$ 和读取路由器 $R_{\text{read}}^{(t)}$。它们根据当前隐藏状态 $\mathbf{h}^{(t)}$ 为每个存储槽位生成归一化的权重：

   \[\mathbf{w}_{\text{write}}^{(t)}=\text{Softmax}(\text{Linear}_{\text{write}}^{(t)}(\mathbf{h}^{(t)})),\quad\mathbf{w}_{\text{read}}^{(t)}=\text{Softmax}(\text{Linear}_{\text{read}}^{(t)}(\mathbf{h}^{(t)}))\]

   这些权重矩阵的维度为 $\mathbb{R}^{L\times B}$，其中 $L$ 是序列长度。

3. MeSH 增强的递归流程:

   • 首先通过核心模块进行计算：$\mathbf{h}_{\text{m}}^{(t)}=f_{\text{core}}(\mathbf{h}^{(t)})$。
   • 然后，使用写入权重 $\mathbf{w}_{\text{write}}^{(t)}$ 将计算结果 $\mathbf{h}_{\text{m}}^{(t)}$ 分布式地写入到缓冲区中的所有槽位：
   \[\mathbf{m}_{b}^{(t+1)}=\mathbf{m}_{b}^{(t)}+\mathbf{h}_{\text{m}}^{(t)}\odot\mathbf{w}_{\text{write},b}^{(t)},\quad\text{for }b=0,\dots,B-1\]
   • 最后，使用读取权重 $\mathbf{w}_{\text{read}}^{(t)}$ 从更新后的缓冲区中加权读取信息，合成下一次迭代的隐藏状态 $\mathbf{h}^{(t+1)}$：
   \[\mathbf{h}^{(t+1)}=\sum_{b=0}^{B-1}\mathbf{m}_{b}^{(t+1)}\odot\mathbf{w}_{\text{read},b}^{(t)}\]

优点

MeSH 的设计直接针对性地解决了递归模型的两大核心病症：

• 通过动态状态组合实现功能专业化: MeSH 的迭代专属路由器 ($R_{\text{write}}^{(t)}, R_{\text{read}}^{(t)}$) 打破了“无差别计算”的僵局。模型在每一步都能学习到如何从包含所有历史状态的记忆缓冲区中，动态地组合出一个特定于当前任务上下文的输入，这使得不同迭代步骤可以学习并执行不同的功能，实现了功能专业化。

• 通过状态外部化缓解信息过载: 外部存储缓冲区 $\mathbf{M}$ 充当了长期信息的高速公路，将隐藏状态 $\mathbf{h}^{(t)}$ 从繁重的记忆任务中解放出来。这使得隐藏状态可以充分利用其全部维度进行复杂的瞬时计算，而关键信息则被安全地保存在缓冲区中并可按需检索，从而避免了维度坍缩，保持了模型全程的表达能力。

实验结论

内部动态诊断分析

本文首先通过内部状态探测，验证了 MeSH 对递归模型病症的修复效果。实验基于 Pythia-410M 模型进行。

• 缓解计算偏斜: 如下图所示，朴素递归 (\(Base\)) 的计算量绝大部分集中在第一次核心循环，而 MeSH 模型实现了显著均衡的计算分布，表明每次迭代都承担了有意义的计算任务。

• 打破表示停滞: CKA 相似度矩阵显示，朴素递归模型在循环中的隐藏状态（$h^{(1)}$, $h^{(2)}$, $h^{(3)}$）之间相似度极高，表明表示陷入停滞。而 MeSH 模型的循环状态之间相似度显著降低，证明其成功打破了不动点吸引子，实现了表示的持续优化。

• 防止表示坍缩: 通过分析隐藏状态矩阵的奇异值谱，发现朴素递归模型的循环状态相比输入状态发生了严重的维度坍缩（谱线衰减更快）。而 MeSH 模型在整个循环过程中都保持了高维度的表示结构，有效避免了信息瓶颈。

主要结果

本文在 160M 至 1.4B 参数规模的 Pythia 模型上进行了广泛实验。递归变体的非嵌入参数比对应的非递归基线少约 33%。

模型规模 (非嵌入)	方案	层配置	版本	Pile PPL↓	Wiki PPL↓	LD-O PPL↓	LD-S PPL↓	0-shot Avg. acc↑	5-shot Avg. acc↑
410M (277M)	Vanilla	12	—	11.31	30.32	42.86	129.89	39.88	40.54
	Recursive (-33%)	2+4R2+2	Base	11.79	32.32	53.06	217.87	38.90 / -0.98	39.29 / -1.25
			+anchor	11.51	31.43	49.33	160.80	38.81 / -1.07	40.15 / -0.39
			+mesh	11.45	31.13	47.16	148.91	39.41 / -0.47	40.60 / +0.06
…	…	…	…	…	…	…	…	…	…
1.4B (1.2B)	Vanilla	24	—	7.44	15.97	10.51	22.81	49.50	51.93
	Recursive (-33%)	4+8R2+4	Base	7.63	16.64	11.38	23.69	48.89 / -0.61	50.99 / -0.94
			+residual	7.58	16.44	10.91	20.44	49.50 / +0.00	51.18 / -0.75
			+anchor	7.51	16.14	10.59	20.37	49.39 / -0.11	51.27 / -0.66
			+mesh	7.39	15.79	10.13	19.39	50.56 / +1.06	52.79 / +0.86

如上表所示，MeSH 增强的递归模型（\(+mesh\)）在所有规模上都一致优于其他递归变体（\(Base\), \(+residual\), \(+anchor\)）。特别是在 1.4B 规模下，MeSH 模型不仅在所有困惑度指标上取得了最佳成绩，甚至在下游任务平均准确率上超越了参数更多的非递归基线模型（0-shot 准确率提升 1.06%，5-shot 提升 0.86%），验证了 MeSH 架构的优越性。

进一步分析

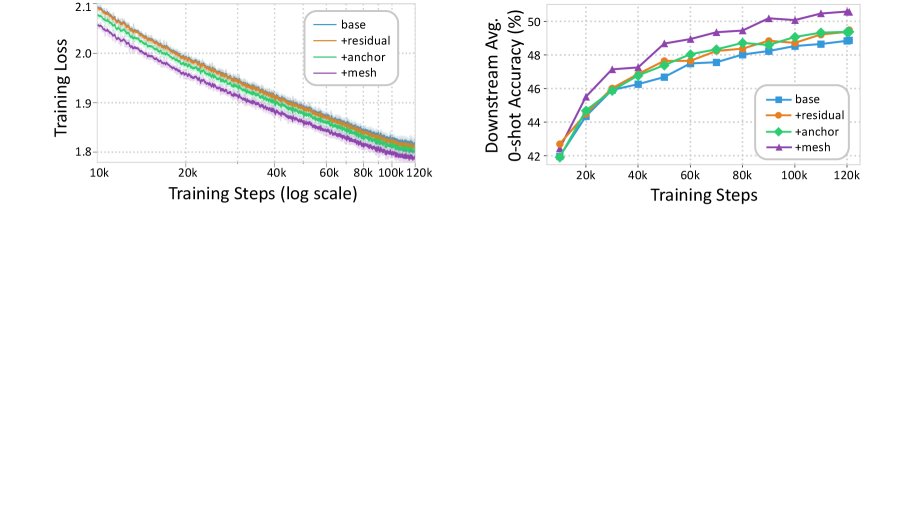
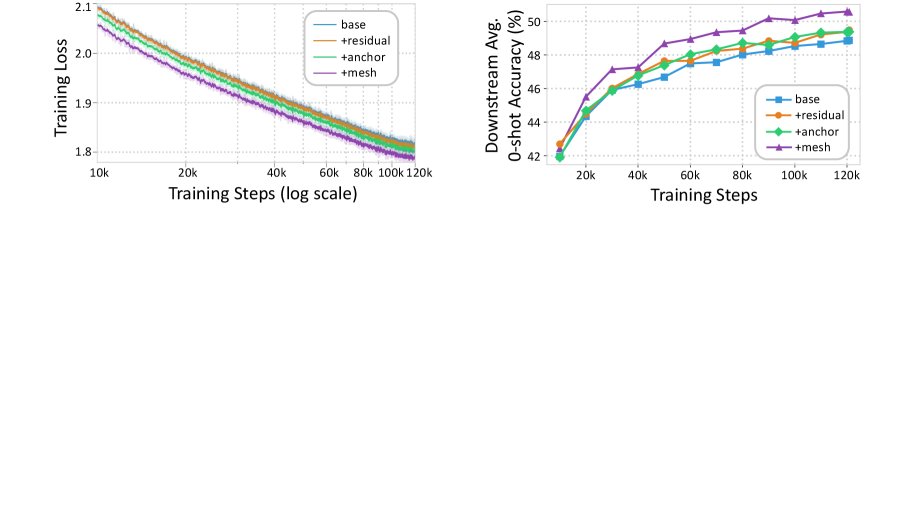
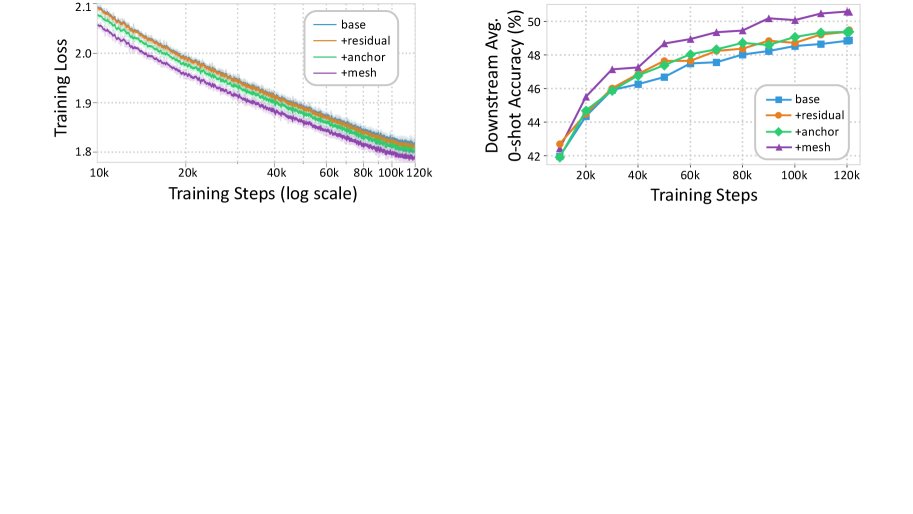
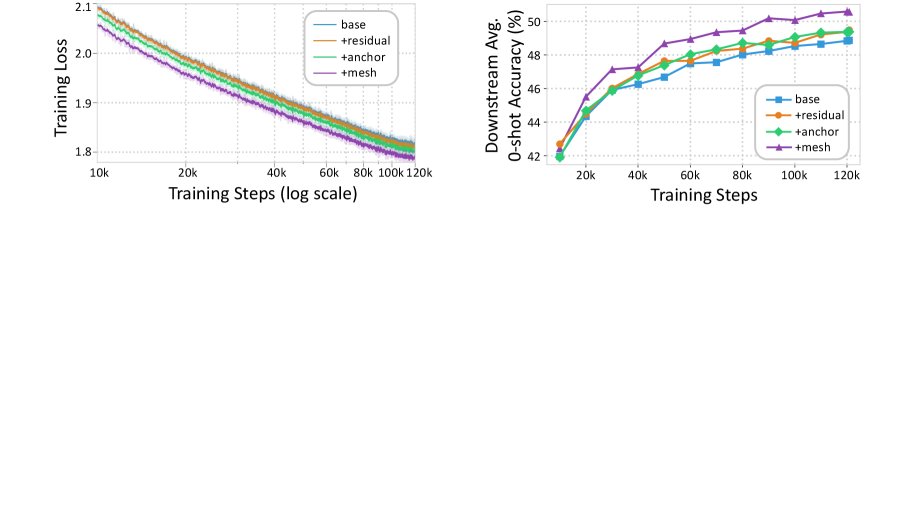
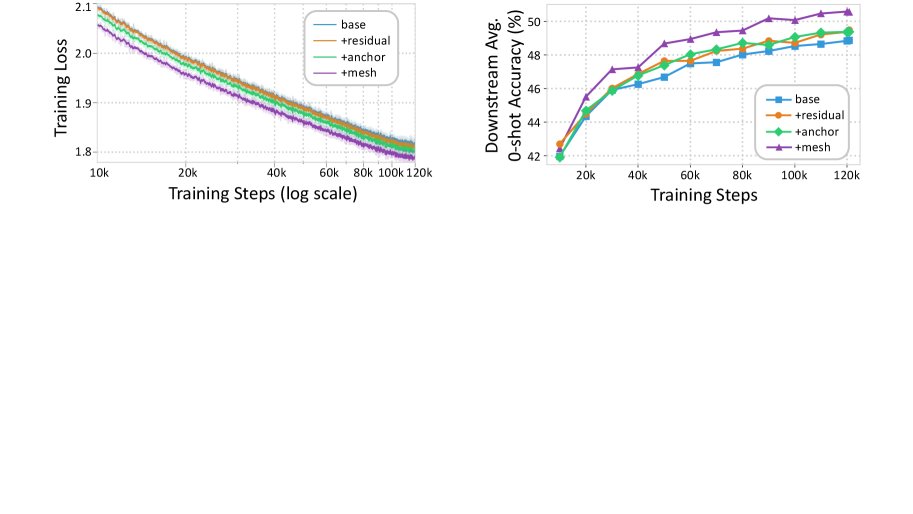
• 训练动态: 如下图所示，MeSH 模型的训练损失在整个预训练过程中持续低于其他变体，并且下游任务准确率的提升也更快、更稳定。这证明 MeSH 的架构优势从训练早期就开始体现，能够实现更高效的学习。

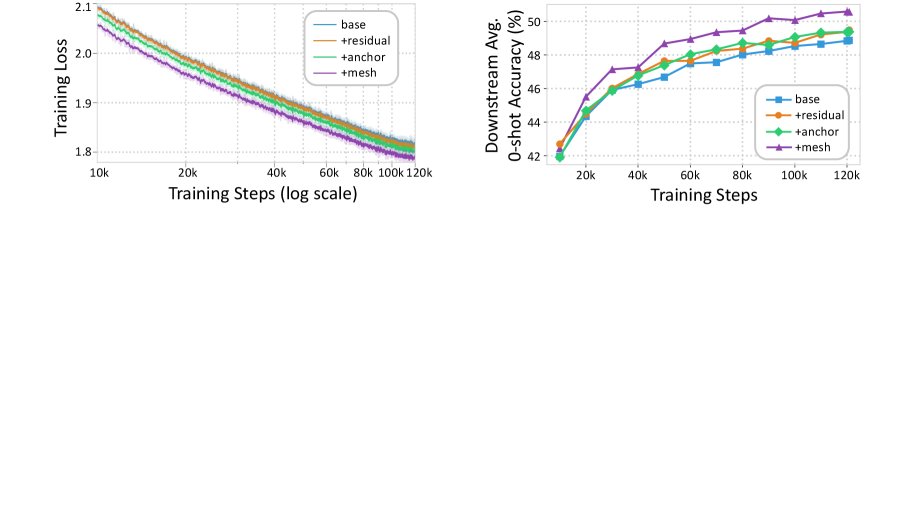
• 参数效率: 缩放曲线表明，朴素递归模型性能远低于同等计算量的非递归基线，而 MeSH 模型不仅弥补了这一差距，甚至在较大规模上实现了反超。例如，参数量为 805M 的 MeSH 模型在下游任务上的表现超过了参数量为 1.2B 的非递归模型，相当于节省了约 33% 的非嵌入参数。

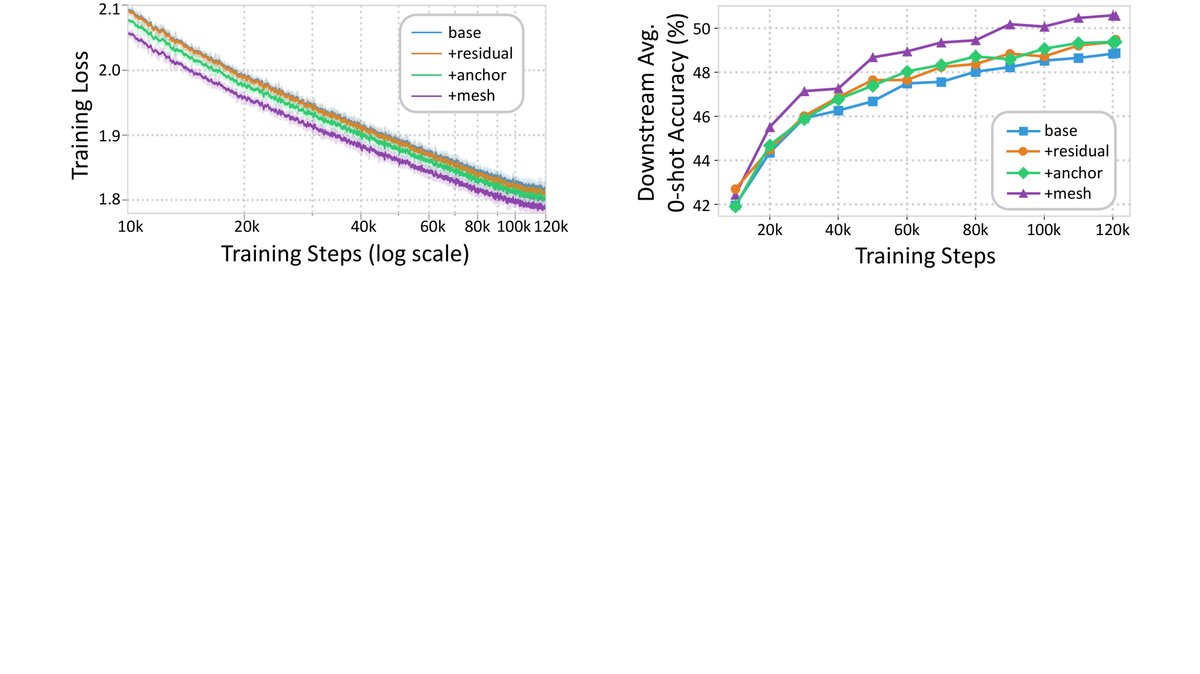
最终结论是，MeSH 作为一个可扩展且有坚实理论基础的架构，为构建更强大的递归模型提供了一条有效的途径，在提升参数效率的同时，也能获得比标准模型更强的性能。