Model Compression using Progressive Channel Pruning

• ArXiv URL: http://arxiv.org/abs/2507.04792v1

• 作者: Wanli Ouyang; Jinyang Guo; Dong Xu; Weichen Zhang

---

TL;DR

本文提出了一种名为渐进式通道剪枝 (Progressive Channel Pruning, PCP) 的迭代式剪枝框架，该框架通过在每次迭代中执行“尝试-选择-剪枝”三步流水线，从多个最优选择的层中逐步移除少量通道，从而自动确定压缩后网络的最优结构，并成功将其应用于监督学习和迁移学习场景。

关键定义

本文提出的核心框架围绕以下几个关键步骤/概念：

• 渐进式通道剪枝 (Progressive Channel Pruning, PCP)：一种新颖的迭代式通道剪枝框架。与一次性、逐层剪枝不同，PCP 在多轮迭代中，每轮只从部分被选中的层中剪去少量通道，通过渐进的方式逐步达到目标压缩率。

• 尝试步骤 (Attempting Step)：在每次迭代中，对于每个可剪枝的卷积层，都“尝试”剪掉预设数量的通道，并基于验证集样本快速评估此次剪枝对模型精度的影响（即精度下降量）。

• 选择步骤 (Selecting Step)：根据“尝试”步骤中获得的各层精度下降信息，采用贪心策略，选出那些剪枝后精度下降最小的若干层（例如\(top_n\)层）。这些层被认为是当前迭代中最具冗余性、最适合剪枝的层。

• 剪枝步骤 (Pruning Step)：对“选择”步骤中确定的层进行永久性剪枝，并更新相关层的权重以补偿剪枝带来的精度损失。未被选中的层在此次迭代中保持不变。

相关工作

当前的深度模型压缩与加速技术主要包括张量分解、量化、优化实现、紧凑网络设计和连接剪枝。其中，通道剪枝作为一种结构化剪枝方法，因其对通用硬件友好而备受关注。

然而，现有的通道剪枝方法存在一些瓶颈：

1. 逐层剪枝的局限性：大多数方法（如 [1, 2]）以逐层方式进行，一次性剪掉目标数量的通道。这使得它们难以确定各层最优的剪枝率，通常需要手动设置或依赖复杂的搜索策略（如强化学习），导致过程繁琐或耗时。
2. 迁移学习场景的缺失：几乎没有工作研究在无监督域适应（Unsupervised Domain Adaptation, UDA）等迁移学习设置下的通道剪枝问题。由于源域和目标域之间存在数据分布差异，仅根据源域数据优化的剪枝策略在目标域上表现不佳。

本文旨在解决上述问题，提出一个能够自动确定各层最优通道数的剪枝框架，并将其创新性地扩展到迁移学习场景，以压缩域适应模型（如 DANN）。

本文方法

本文提出了渐进式通道剪枝（PCP）框架，首先介绍了其在标准监督学习下的工作原理，然后将其扩展到更具挑战性的迁移学习（无监督域适应）场景。

监督学习下的PCP方法

PCP的核心思想是通过一个迭代式的“尝试-选择-剪枝”三步流水线，以贪心策略逐步逼近最优的剪枝后网络结构。

创新点

方法的核心是一个迭代循环，直到达到目标压缩率 $R_{target}$。在第 $t$ 次迭代中：

1. 尝试 (Attempting) 步骤: 对每个待剪枝的第 $l$ 层，系统会尝试剪去一小部分（如 $\mathrm{f}_t$ 个）通道。具体来说，通过求解一个LASSO回归问题来临时确定要剪掉的通道，并用最小二乘法重构该层权重。然后，在验证集上评估这个临时修改后的模型的精度，记录下其精度下降值。这一步的目的是探查每一层对剪枝的“敏感度”。

2. 选择 (Selecting) 步骤: 收集所有层的尝试剪枝结果后，选择精度下降最小的 \(top_n\) 个层。这些层被认为是当前冗余度最高、最适合剪枝的层。将这些被选中层的索引按从浅到深的顺序存入集合 $\mathbf{S}_{t}$。

3. 剪枝 (Pruning) 步骤: 仅对 $\mathbf{S}_{t}$ 中的层进行永久性剪枝。系统会按照从浅到深的顺序，依次对每个选中的层求解 LASSO 问题以确定最终剪枝的通道，并用最小二乘法更新权重。这种顺序更新使得深层网络可以适应浅层剪枝带来的输入特征变化。未被选中的层在此次迭代中保持不变。

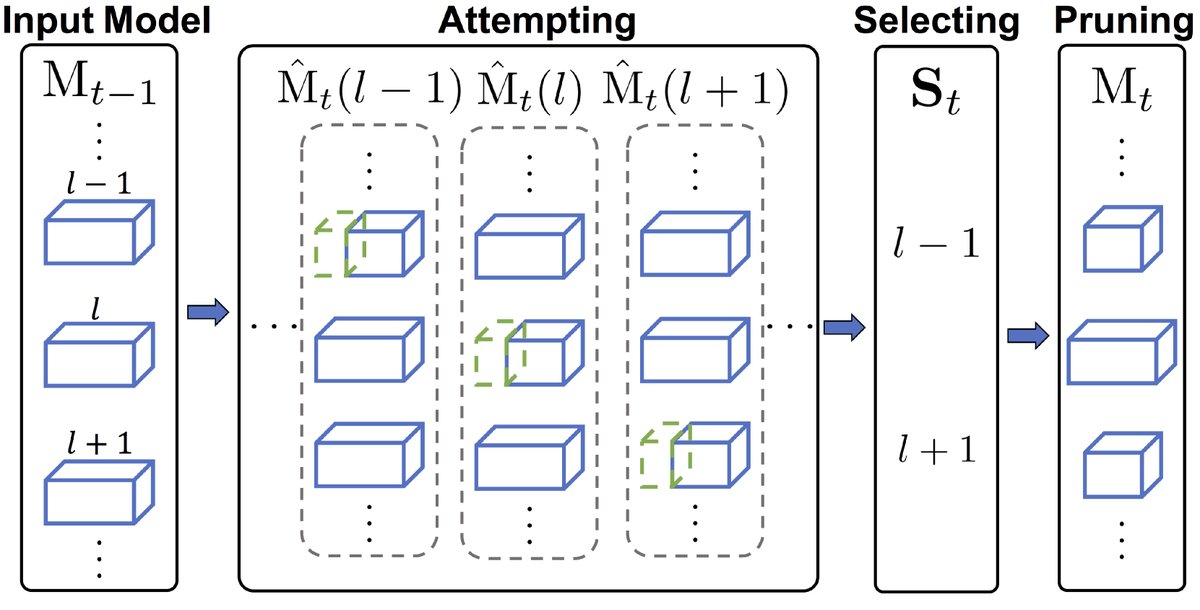
该迭代过程（如算法1所示）不断重复，模型被逐步压缩。每轮迭代结束后的模型都可以被保存下来，从而自然地获得一系列不同压缩率的压缩模型，适用于可伸缩应用。

对残差结构的处理

对于ResNet这类具有残差连接的架构，本文采用了特殊处理策略：

• 剪枝残差块的第一个卷积层: 为避免破坏残差连接的加法操作（要求特征图维度一致），本文引入一个“通道采样器”（channel sampler）来对输入特征图进行降维，而不是直接修改输入。
• 剪枝残差块的最后一个卷积层: 为了补偿因剪枝累积的误差，优化目标被修改，以同时考虑主分支和捷径分支的输出，减少误差累积。

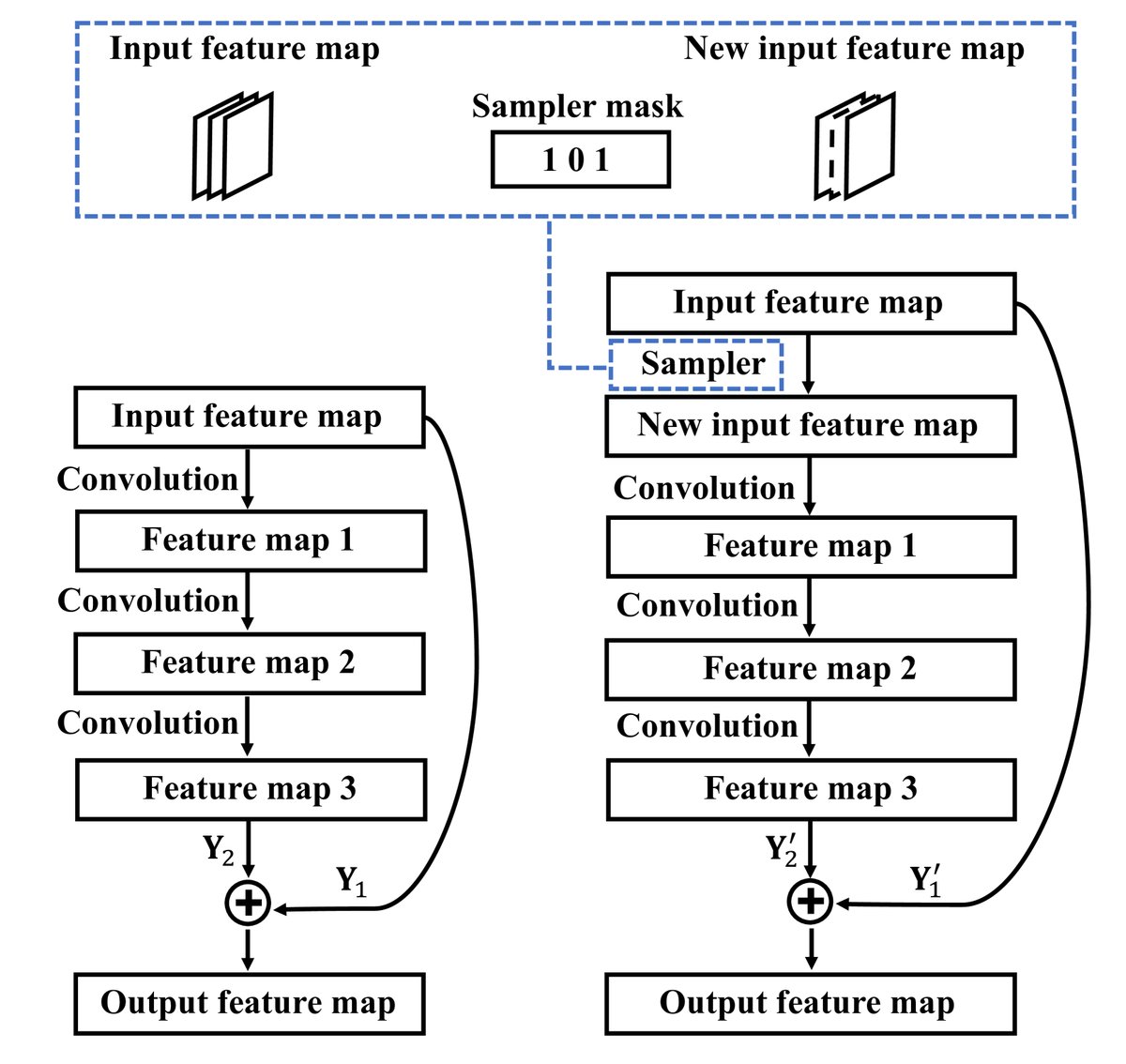
在整个剪枝流程结束后，最终得到的压缩模型会通过在所有训练数据上进行标准的微调 (Fine-tuning) 来恢复性能。

迁移学习下的PCP扩展

本文的一大贡献是将PCP框架扩展到无监督域适应（以DANN模型为例）的场景中。在UDA中，模型需要处理带标签的源域数据和无标签的目标域数据。

创新点

为解决域漂移（domain shift）问题，本文对PCP进行了两项关键调整：

1. 利用目标域数据生成伪标签: 首先，使用一个在源域和目标域上预训练好的完整DANN模型，为无标签的目标域样本生成伪标签 (pseudo-labels)。在PCP的“尝试”步骤中，模型精度的评估同时在带标签的源域样本和带伪标签的目标域样本上进行。这使得剪枝决策能够兼顾两个域的数据分布，找到对两个域都更优的剪枝方案。

2. 选择信息丰富的特征: 在UDA任务中，由于背景等因素差异，特征图的很多空间位置可能是无信息量的。因此，在求解LASSO等优化问题时，本文提出只选择那些在所有通道上方差较大的空间位置的特征进行计算，从而避免了背景等无信息区域的干扰，使权重重构更关注于有意义的特征。

整个流程包括：首先预训练一个DANN模型，然后使用带有上述两项改进的PCP框架对其进行剪枝，最后再使用DANN方法对剪枝后的模型进行微调。

实验结论

（注：原文的实验部分内容不完整，以下结论基于论文前文的声明和方法论的预期效果。）

本文在ImageNet和Office-31等标准数据集上，分别对监督学习和无监督域适应两种设置下的PCP框架进行了验证。

• 方法优势验证：实验结果清晰地表明，无论是在监督学习还是迁移学习设置下，PCP框架的表现都优于现有的其他通道剪枝方法。
• 最佳效果场景：PCP的核心优势在于其能够自动发现各层合适的剪枝率，从而在相同的模型压缩率下获得更高的分类精度。尤其是在UDA场景下的扩展，是本文的独特贡献，有效解决了压缩迁移学习模型这一实际难题。
• 可扩展性：PCP的迭代特性使其能够自然地生成一系列不同压缩率的有效模型（例如，在以5x为目标时，可以顺带得到2x、3x、4x的压缩模型），这对于需要根据设备性能动态调整模型大小的应用非常有价值。
• 最终结论：本文提出的PCP框架是一个简单而高效的模型压缩方法。其渐进式的贪心搜索策略成功地将寻找最优网络结构的过程自动化。通过引入伪标签和信息特征选择，该框架被成功扩展到具有挑战性的域适应任务中，展示了其强大的通用性和有效性。