Not All Parameters Are Created Equal: Smart Isolation Boosts Fine-Tuning Performance

TL;DR

本文提出了一种名为“核心参数隔离微调”（CPI-FT）的新框架，通过识别并隔离每个任务的核心参数区域、根据区域重叠度对任务进行分组，并结合参数融合与动态冻结策略进行多阶段微调，从而有效缓解多任务监督微调中的任务冲突和灾难性遗忘问题。

关键定义

本文提出了几个核心概念来构建其微调框架：

相关工作

目前，监督式微调 (Supervised fine-tuning, SFT) 是使大型语言模型（LLMs）适应下游任务的关键方法。然而，在处理包含多种异构任务（如数学推理、编码、创意写作等）的场景时，SFT面临着严峻的挑战。

现有方法的主要瓶颈在于“跷跷板效应” (seesaw effect)，即在某个任务上取得的进展往往以牺牲其他任务的性能为代价。传统的联合多任务微调或多阶段微调等方法，通常不加区分地更新所有模型参数，未能考虑到不同任务对参数的依赖性差异。这种统一更新的策略加剧了任务间的梯度冲突和灾难性遗忘 (catastrophic forgetting)，阻碍了模型泛化能力的提升。

本文旨在解决的核心问题是：如何在多任务监督微调中，系统性地缓解任务间的负面干扰和灾难性遗忘。作者认为，问题的根源在于“参数异质性”，即不同任务依赖于模型中不同的参数子集。因此，本文的目标是提出一种能够识别并保护这些任务专属参数区域的微调范式，实现对微调过程更精细的控制。

本文方法

本文提出了核心参数隔离微调（CPI-FT）框架，旨在通过系统地识别、隔离和保护任务特定的参数区域，来解决多任务微调中的干扰和遗忘问题。该框架包含以下四个核心阶段：

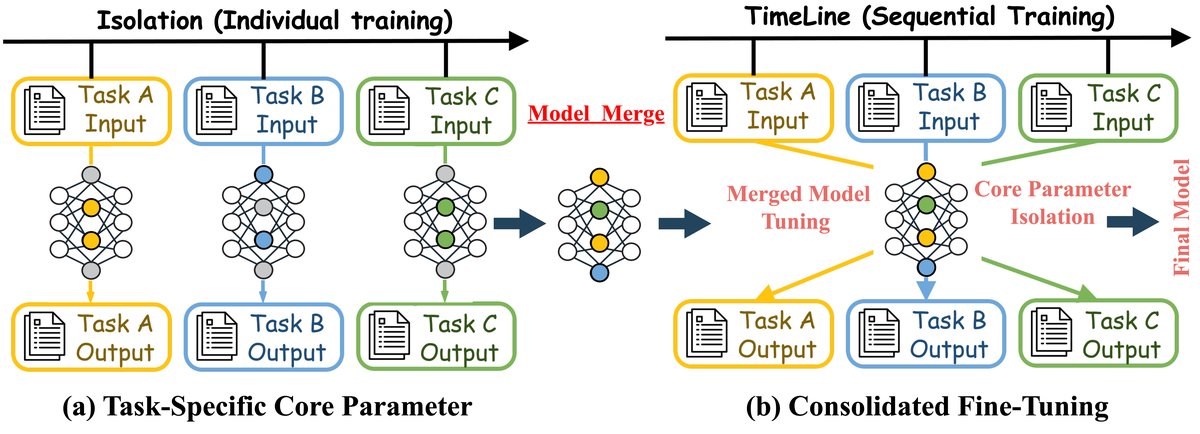CPI-FT框架流程图 图1：该图说明了(a) 任务特定的核心参数隔离方法和(b) 整合微调方法。在隔离方法中，每个任务单独训练，然后将模型合并。而在时间线方法中，任务按顺序处理，然后进行合并和微调，最终生成一个统一模型。

阶段一：识别任务特定的核心参数区域

此阶段的目标是为每个任务识别出其专属的“核心参数区域”。

  1. 独立微调探测：对于 $N$ 个任务 $T_1, …, T_N$ 中的每一个，从同一个预训练模型 checkpoint $\theta^{(0)}$ 开始，仅使用该任务的数据 $\mathcal{D}_i$ 进行独立的、短暂的微调，得到任务特定的模型参数 $\theta^{(i)}$。

  2. 计算更新幅度：通过计算每个参数 $j$ 在微调前后的绝对差值来量化其重要性：

    \[\Delta \mid \theta^{(i)}_{j} \mid = \mid \theta^{(i)}_{j}-\theta^{(0)}_{j} \mid\]

    作者认为，更新幅度直接反映了参数为适应特定任务而偏离初始状态的程度，相比于梯度幅值等指标更稳定且计算高效。

  3. 定义核心区域：对于每个任务 $T_i$，其核心参数区域 $C_i$ 被定义为更新幅度最大的前 $p\%$ 的参数集合。

    \[C_{i}=\text{arg topk}_{j\in\{1..D\}}(\Delta \mid \theta^{(i)}_{j} \mid ,\lfloor p\cdot D/100\rfloor)\]

    这里的 $p$ 是一个超参数，控制核心区域的大小。

阶段二：基于核心区域相似度的任务分组与排序

为了减少相似任务间的直接冲突，本文根据它们核心参数区域的重叠程度对任务进行分组。

  1. 计算相似度：使用杰卡德指数 (Jaccard Index) 来度量任意两个任务 $T_i$ 和 $T_j$ 的核心区域 $C_i$ 和 $C_j$ 的相似度：

    \[S(C_{i},C_{j})=\frac{ \mid C_{i}\cap C_{j} \mid }{ \mid C_{i}\cup C_{j} \mid }\]
  2. 任务分组：基于一个相似度阈值 $\tau$，如果 $S(C_i, C_j) \geq \tau$，则任务 $T_i$ 和 $T_j$ 被认为是相关的。最终，通过计算任务相似度图中的连通分量，将所有任务划分到不同的组 $G_1, …, G_K$ 中。
  3. 确定阶段顺序：将任务组排列成一个序列 $(G_1, G_2, …, G_K)$，用于后续的多阶段微调。本文主要评估了随机排序。

阶段三：跨任务的参数融合

这一创新阶段旨在将从各个任务中学到的知识整合到一个统一的模型中。

  1. 选择基础模型：选用最后一个微调阶段得到的模型参数 $\theta_{\text{base}}$ 作为融合的起点。

  2. 核心参数覆盖：对于每个任务 $T_i$，将其在独立微调中确定的核心参数 $\theta^{(i)}$ 的值，直接“移植”到基础模型 $\theta_{\text{base}}$ 的相应位置。这确保了每个任务的关键能力被无损保留。

    \[\theta_{\text{fused},j}=\begin{cases}\theta^{(i)}_{j}&j\in C_{i}\\ \theta_{\text{base},j}&j\notin C_{i}\end{cases}\]

  3. 非核心参数融合：对于不属于任何核心区域的参数，为了避免冲突并保证模型平滑过渡，采用球面线性插值（SLERP）进行融合。该方法能以几何感知的方式平滑地混合来自不同任务的知识。

    \[\theta_{\text{fused},j}=\begin{cases}\omega\theta^{(i)}_{j}+(1-\omega)\theta_{\text{base},j},&\angle(\theta_{\text{base},j},\theta^{(i)}_{j})<\epsilon\\ \text{SLERP}(\theta_{\text{base},j},\theta^{(i)}_{j},\omega),&\text{otherwise}\end{cases}\]

    其中 $\omega$ 是插值因子，$\epsilon$ 是判断向量是否共线的阈值。

阶段四：通过多阶段训练进行整合微调

最后，对融合后的模型进行一次精简的多阶段微调，以巩固其泛化能力。

  1. 动态冻结机制：在微调过程中，所有先前阶段识别出的核心参数区域都会被冻结。具体来说，当训练第 $k$ 个任务组 $G_k$ 时，所有来自前 $k-1$ 个任务组的核心参数都不可更新。这通过一个二进制掩码 $M_k$ 实现。

    \[\Delta\theta_{t+1}=\theta_{t}+\Delta\theta_{t}\odot M_{k}\]
  2. 采样数据校准：此阶段不使用全部数据，而是从每个任务中抽取一小部分数据构成平衡的混合训练集，以提高效率并防止过拟合。
  3. 多阶段训练流程：按照阶段二确定的顺序，依次在每个任务组 $G_k$ 的采样数据上进行微调，同时应用动态冻结机制。最终得到的模型 $\theta_{\text{final}}$ 整合了所有任务的知识，同时有效避免了相互干扰。

实验结论

本文通过在多个基准和模型上的广泛实验，验证了CPI-FT框架的有效性。

主要性能对比

实验结果表明，CPI-FT在所有测试的基座模型（LLaMA-2-7B, Mistral-8B, Qwen1.5-7B, Gemma-9B）和任务（GSM8K, CodeAlpaca, LogiQA, Alpaca, UltraChat）上，其性能都显著优于标准的联合多任务微调（Full SFT）和多阶段微调基线。这证明了CPI-FT在缓解任务冲突方面的普遍有效性。

基座模型 方法 GSM8K CodeAlpaca LogiQA Alpaca UltraChat 平均归一化得分
LLaMA-2-7B Full SFT (Multi-task) 48.2 25.1 55.3 7.1 7.5 6.58
  Multi-Stage (Random, K=3) 49.5 24.8 56.0 7.3 7.6 6.70
  Multi-Stage (Heuristic) 50.1 25.5 56.8 7.0 7.4 6.75
  CPI-FT (本文方法, p=1%, $\tau$=0.1) 53.5 27.2 59.1 7.6 7.8 7.21
Mistral-8B Full SFT (Multi-task) 46.5 24.0 53.8 6.9 7.3 6.37
  Multi-Stage (Random, K=3) 47.8 23.7 54.5 7.1 7.4 6.49
  Multi-Stage (Heuristic) 48.3 24.3 55.2 6.8 7.2 6.53
  CPI-FT (本文方法, p=1%, $\tau$=0.1) 51.6 25.9 57.4 7.5 7.7 6.98
Qwen1.5-7B Full SFT (Multi-task) 49.8 26.0 56.5 7.3 7.7 6.79
  Multi-Stage (Random, K=3) 51.0 25.7 57.3 7.5 7.8 6.92
  Multi-Stage (Heuristic) 51.7 26.4 58.0 7.2 7.6 6.98
  CPI-FT (本文方法, p=1%, $\tau$=0.1) 55.3 28.1 60.6 7.8 8.1 7.45
Gemma-9B Full SFT (Multi-task) 51.5 27.2 58.0 7.6 8.0 7.05
  Multi-Stage (Random, K=3) 52.8 26.9 58.9 7.8 8.1 7.19
  Multi-Stage (Heuristic) 53.5 27.6 59.7 7.5 7.9 7.26
  CPI-FT (本文方法, p=1%, $\tau$=0.1) 57.2 29.4 62.5 8.1 8.4 7.73

表1：不同方法在各项SFT任务上的主要性能对比。

灾难性遗忘分析

在序贯微调（先训练任务A，再训练任务B）的场景下，CPI-FT（在表中称为DPI）展现出卓越的抗遗忘能力。相比于Full SFT高达24.5分的性能下降，CPI-FT仅下降5.7分，减少了超过65%的遗忘，同时还能很好地学习新任务。

方法 A$\rightarrow$B   B$\rightarrow$A  
  $\Delta$A ($\downarrow$) $\Delta$B ($\uparrow$) $\Delta$B ($\downarrow$) $\Delta$A ($\uparrow$)
Full SFT -24.5 +13.4 -16.7 +20.2
Multi-Stage SFT -16.2 +12.6 -12.3 +17.5
CPI-FT (本文方法) -5.7 +12.2 -4.8 +18.8

表2：在LLaMA-2-7B上进行的序贯微调灾难性遗忘分析。

其他分析与结论

最终结论：本文提出的CPI-FT框架通过识别和隔离任务的核心参数区域，成功地缓解了多任务SFT中的“跷跷板效应”和灾难性遗忘。它为在异构任务场景下进行稳健的模型微调提供了一种可扩展且有效的方法。