On the Theoretical Limitations of Embedding-Based Retrieval

• ArXiv URL: http://arxiv.org/abs/2508.21038v1

• 作者: Jinhyuk Lee; Orion Weller; Iftekhar Naim; Michael Boratko

• 发布机构: Google DeepMind; Johns Hopkins University

---

TL;DR

本文通过连接学习理论与嵌入式检索，从理论和实证上证明了单向量嵌入模型因其维度限制，无法表示所有可能的相关文档组合，并构建了一个名为LIMIT的简单数据集，揭示了即使是当前最先进的模型也存在这一根本局限性。

关键定义

本文的核心论证建立在对检索问题和向量表征能力的数学形式化之上，关键定义如下：

• 行序保持秩 (row-wise order-preserving rank, \($\operatorname{rank}\_{\text{rop}} A\)$): 对于一个给定的$m \times n$的相关性矩阵$A$，此秩是能产生一个$m \times n$得分矩阵$B$的最小嵌入维度$d$（即$B$的秩），使得$B$中每一行的元素顺序都与$A$中对应行的顺序一致。简而言之，就是能够为所有查询正确排序相关和不相关文档所需的最小嵌入维度。
• 行级可阈值分离秩 (row-wise thresholdable rank, \($\operatorname{rank}\_{\text{rt}} A\)$): 最小嵌入维度$d$，使得存在一个秩为$d$的得分矩阵$B$，并且对每一行（每个查询）都存在一个阈值$\tau_i$，能将相关文档的得分与不相关文档的得分完全分开。
• 全局可阈值分离秩 (globally thresholdable rank, \($\operatorname{rank}\_{\text{gt}} A\)$): 最小嵌入维度$d$，使得存在一个秩为$d$的得分矩阵$B$，并且存在一个单一全局阈值$\tau$，能将所有查询中相关文档的得分与不相关文档的得分完全分开。
• 符号秩 (Sign Rank, \($\operatorname{rank}\_{\pm} M\)$): 一个在通信复杂度理论中已有的概念。对于一个元素为-1或1的矩阵$M$，其符号秩是与$M$具有相同正负号模式的任意实数矩阵$B$的最小可能秩。本文将检索模型的表征能力与符号秩建立了直接联系。

相关工作

当前，基于神经网络的嵌入模型（即稠密检索）正被用于解决日益复杂的检索任务，如指令遵循（instruction-following）和多模态检索。社区的普遍趋势是推动模型能够处理“任何查询”和“任何形式的相关性定义”，这隐含地假设了嵌入模型具有无限的表征能力。

然而，现有的学术基准（如MTEB, QUEST）由于标注成本等原因，通常只包含有限数量的查询，这些查询仅覆盖了所有可能的相关文档组合中的极小一部分，从而掩盖了嵌入模型潜在的表征瓶颈。虽然有研究从经验上探讨过维度的影响，但缺乏一个坚实的理论基础来解释其根本限制。

本文旨在填补这一空白，具体解决的问题是：单向量嵌入模型在表征所有可能的top-k相关文档组合方面，是否存在根本的、理论上的限制？这个限制与嵌入维度$d$有何关系？以及这种理论限制是否会在现实中以简单的形式出现？

本文方法

理论基础与形式化

本文首先将检索问题数学化。给定$m$个查询和$n$个文档，其相关性可以用一个二元矩阵 $A \in {0, 1}^{m \times n}$ 表示（在信息检索中称作qrels）。嵌入模型将查询$i$映射为向量$u_i \in \mathbb{R}^d$，文档$j$映射为$v_j \in \mathbb{R}^d$。检索得分通过点积 $u_i^T v_j$ 计算。所有得分构成一个得分矩阵 $B = U^T V$，其秩最大为$d$。

本文的核心理论贡献在于将“能够正确检索”这一要求与矩阵的秩联系起来，并引入了上文定义的\(rop-rank\)、\(rt-rank\)等概念。通过一系列证明，得出了以下关键关系：

\[\operatorname{rank}_{\pm}(2A-\mathbf{1}_{m\times n})-1 \leq \operatorname{rank}_{\text{rop}}A = \operatorname{rank}_{\text{rt}}A \leq \operatorname{rank}_{\text{gt}}A \leq \operatorname{rank}_{\pm}(2A-\mathbf{1}_{m\times n})\]

这个不等式链条将嵌入模型所需的最小维度$d$（即\(rop-rank\)）与相关性矩阵$A$的符号秩（\(sign-rank\)）紧密地绑定在一起。

创新点

本文的本质创新在于，它没有提出一种新模型，而是从理论层面揭示了现有范式的天花板。其核心思想是：

1. 连接理论与实践：首次将通信复杂度理论中的“符号秩”概念引入现代神经信息检索领域，为分析嵌入模型的表征能力提供了坚实的数学工具。
2. 证明根本限制：证明了对于任意给定的嵌入维度$d$，总存在一些相关文档的组合（即一个qrel矩阵$A$），是d维嵌入模型无法完美表示的。这是因为qrel矩阵的符号秩可以任意高，而模型的表征能力受限于维度$d$。

基于理论的实证与数据集构建

为了验证理论并展示其在现实世界中的影响，本文设计了两层实证研究。

最佳情况下的优化实验

为了排除自然语言建模等混淆因素，本文设计了一个“自由嵌入（free embedding）”优化实验。在该实验中，查询和文档的向量本身就是可直接优化的参数，目标是直接拟合一个给定的qrel矩阵。这代表了任何嵌入模型能达到的性能上限。

• 实验设置: 对于给定的嵌入维度$d$和top-k的$k$值（本文设$k=2$），逐步增加文档数量$n$，直到模型无法再100%准确地表示所有$\binom{n}{k}$种相关文档组合。这个临界点被称为critical-n。
• 结果: 实验发现，critical-n与维度$d$之间存在一个三次多项式关系。根据该关系外推，即使是4096维的嵌入，在理想情况下也只能处理约2.5亿文档的所有top-2组合，这对于网络规模的语料库是远远不够的。

LIMIT数据集

为了在真实的自然语言环境中复现上述理论限制，本文构建了一个名为LIMIT (Limitations of Instructions & Meaning In Text) 的新数据集。

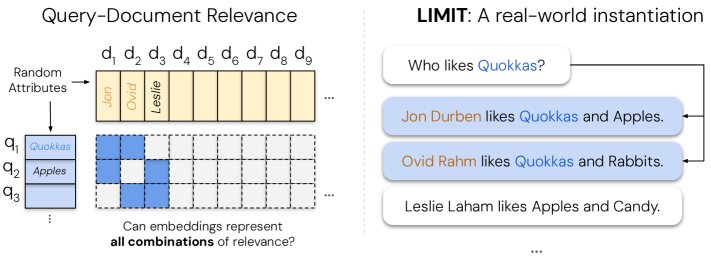
• 构建思想：创建一个在语义和词汇上极其简单，但在组合上极其复杂的任务。这能有效隔离模型的表征能力瓶颈，而非其语言理解能力。
• 构建过程：
  1. 选择困难的qrel模式：理论推断，当一个qrel矩阵包含尽可能多的文档组合时，其符号秩最高，对模型挑战最大。因此，选择了一个覆盖了46个文档所有top-2组合的qrel矩阵（共$\binom{46}{2} = 1035$个查询）。
  2. 实例化为自然语言：将这个抽象的qrel矩阵映射为简单的“属性偏好”任务。查询是“谁喜欢X？”（如“谁喜欢苹果？”），文档是“Jon喜欢苹果、香蕉…”等形式。
  3. 增加难度：将这46个“核心”文档嵌入到一个包含5万个文档的语料库中，其余文档作为干扰项。同时，也提供一个仅包含46个核心文档的“small”版本。
• 优点：LIMIT数据集的巧妙之处在于，它对于BM25这类高维稀疏模型来说非常简单（因为它依赖词汇匹配），但对于依赖低维稠密向量表征语义的嵌入模型则构成了巨大挑战。

实验结论

本文在一系列SOTA嵌入模型上对LIMIT数据集进行了评估，并进行了深入分析。

主要发现

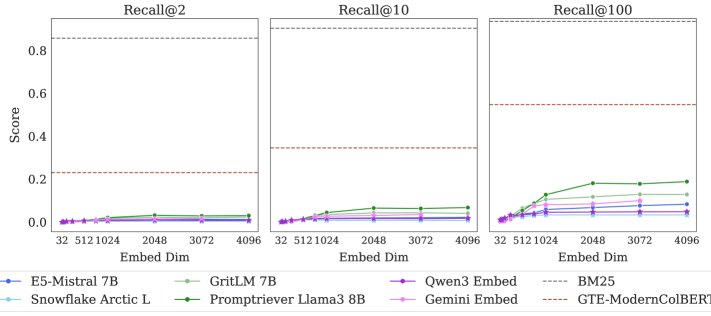
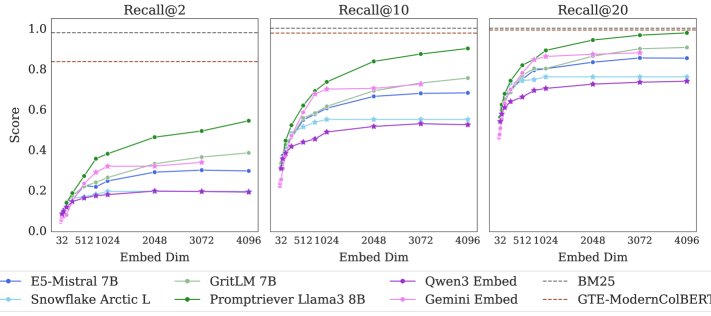
• SOTA模型惨败：在LIMIT数据集上，所有单向量嵌入模型表现极差。在5万文档的完整版上，即便是最好的模型，Recall@100也不足20%。在仅有46个文档的small版本上，模型也无法完全解决任务（Recall@20都无法达到100%）。这证明了理论限制在实际中确实存在且影响巨大。
• 维度是关键因素：模型性能与嵌入维度$d$显著正相关。维度越高，性能越好，但离解决任务仍相去甚远。这与理论预测完全一致。
• 替代架构表现优越：
  • 稀疏模型：BM25由于其等效于超高维向量空间，几乎完美地解决了该任务。
  • 多向量模型：如ColBERT，其性能显著优于所有单向量模型，展示了更强的表征能力。
  • 重排器：长上下文重排模型（如Gemini 2.5 Pro）能够一次性处理所有文档和查询，并100%正确地完成任务，说明该任务本身在逻辑上并不难，瓶颈在于第一阶段检索的表征方式。

进一步分析

• 并非领域偏移：实验证明，在LIMIT风格的训练集上进行微调对模型性能提升甚微。然而，如果直接在测试集上进行训练（过拟合），模型则可以学会任务。这表明性能低下是由于任务的内在组合难度，而非模型不适应数据领域。

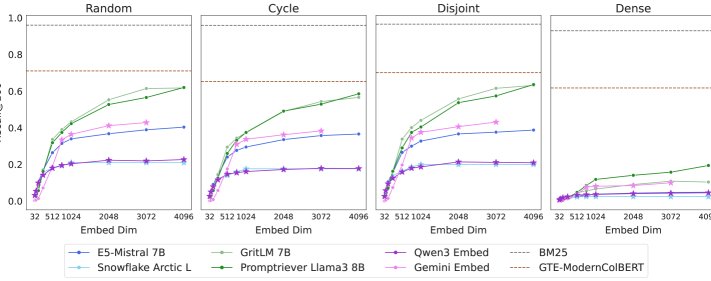
• qrel模式的重要性：通过构建具有不同qrel模式（如随机、循环、不相交）的LIMIT变体进行对比，实验发现本文采用的“稠密”组合模式（即包含所有$\binom{n}{k}$组合）确实比其他模式困难得多，这验证了数据集设计的核心假设。

• 与主流基准无相关性：模型在LIMIT上的表现与在BEIR（MTEB-v1的核心）上的表现没有明显相关性，这表明现有主流基准可能没有充分测试模型的组合表征能力，模型可能已经对这些基准过拟合。

总结

本文的实验结果有力地证实了其理论预测：单向量嵌入模型存在一个由其维度决定的根本性表征上限。随着检索任务（尤其是指令遵循任务）变得越来越复杂，需要模型能够区分和组合前所未有的文档集合，这一理论限制将成为一个严峻的现实瓶颈。因此，社区在评估和设计下一代检索系统时，应充分意识到这一局限，并积极探索如多向量、稀疏表示或混合模型等更具表征力的架构。