Online Process Reward Leanring for Agentic Reinforcement Learning
-
ArXiv URL: http://arxiv.org/abs/2509.19199v2
-
作者: Jianbin Jiao; Ke Wang; Fei Huang; Xiaoqian Liu; Yongbin Li; Junge Zhang; Yuchuan Wu
-
发布机构: Chinese Academy of Sciences; Tongyi Lab; University of Chinese Academy of Sciences
TL;DR
本文提出了一种名为在线过程奖励学习 (Online Process Reward Learning, OPRL) 的智能体强化学习信誉分配策略,该策略通过在线交替优化一个过程奖励模型和智能体策略,将轨迹级别的偏好无缝转化为密集的步骤级奖励,从而在不依赖额外数据或步骤标签的情况下,高效稳定地训练长时程大型语言模型(LLM)智能体。
关键定义
本文的核心是围绕在线学习得到的隐式步骤奖励来展开的,关键定义如下:
- 在线过程奖励学习 (Online Process Reward Learning, OPRL):一种通用的智能体强化学习(RL)信誉分配策略。它与标准的在线(on-policy)RL算法无缝集成,通过在线训练一个过程奖励模型(PRM),将轨迹级的偏好信号转化为步骤级的密集奖励,用于指导策略更新。
- 过程奖励模型 (Process Reward Model, PRM):一个与智能体策略交替优化的语言模型。在OPRL中,这是一个隐式模型,它不直接预测一个分数,而是通过其在动作上的概率分布来体现奖励。此PRM通过一个基于DPO(Direct Preference Optimization)的目标函数,从轨迹对的偏好中学习。
-
隐式步骤奖励 (Implicit Step Rewards):OPRL的核心产出。对于在$t$时刻的动作$a_t$,其隐式步骤奖励被定义为:
\[r_{\phi}(o_{1:t}, a_{t}) = \beta \log \frac{\pi_{\phi}(a_{t} \mid o_{1:t}, x)}{\pi_{\theta_{\text{old}}}(a_{t} \mid o_{1:t}, x)}\]其中,$\pi_{\phi}$是当前更新的PRM,$\pi_{\theta_{\text{old}}}$是上一轮的策略模型快照。这个奖励衡量了在PRM看来,当前动作相比旧策略有多大的改进,从而为策略学习提供密集的指导信号。
相关工作
当前,在动态、交互式环境中训练大型语言模型(LLM)智能体面临巨大挑战,主要瓶颈包括:
- 稀疏奖励和信誉分配:环境奖励通常在任务结束时才给出,导致难以判断中间步骤的贡献,即存在时序信誉分配(temporal credit assignment)难题。
- 高方差学习:智能体的轨迹长且复杂,在 token 层面进行奖励分配会引入巨大噪声,导致策略学习的方差过高、训练不稳定。
- 开放环境的复杂性:在开放式环境(如对话)中,状态空间巨大且几乎不重叠,奖励信号往往难以验证,这使得许多传统RL方法失效。
已有的过程监督方法存在各自的局限性:
- 人工标注或启发式规则:成本高、存在偏见,且容易被智能体利用规则漏洞(reward hacking)。
- 生成式奖励模型(GRMs):例如使用LLM作为评审,其给出的步骤级反馈可能充满噪声且在不同领域间不一致。
- Token级PRM:虽然在单轮任务中有效,但对于长轨迹的智能体任务,其奖励信号过于细粒度,会放大方差,破坏训练稳定性。
- 状态分组方法:依赖于在不同轨迹中出现完全相同的状态,这在状态空间巨大的语言环境中几乎不可能实现。
本文旨在解决上述问题,提出一个通用的、无需步骤级标签、高效且稳定的信誉分配策略,以适应具有稀疏、延迟甚至不可验证奖励的长时程智能体任务。
本文方法
本文提出的在线过程奖励学习(OPRL)框架,通过在线学习一个过程奖励模型(PRM),将稀疏的轨迹级结果偏好转化为密集的步骤级奖励信号,从而指导策略的精细化更新。
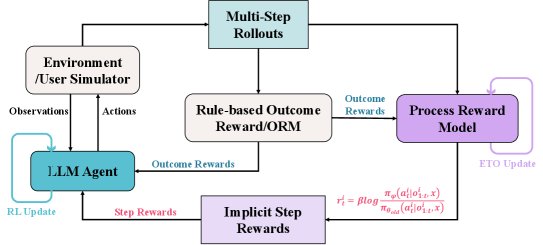
上图展示了 OPRL 的整体训练流程:智能体与环境交互产生轨迹,一个结果奖励模型(ORM)评估整个轨迹并给出结果奖励。这些带有结果标签的轨迹被用来更新PRM,PRM再为轨迹中的每一步生成隐式过程奖励。最终,智能体的策略利用结果奖励和隐式步骤奖励进行更新。
核心流程
OPRL的训练过程是一个策略模型 $\pi_{\theta}$ 和过程奖励模型 $\pi_{\phi}$ 交替优化的自增强循环:
- 数据采样:使用当前策略 $\pi_{\theta}$ 与环境交互,生成一批轨迹。
-
PRM优化:根据轨迹的结果奖励(由验证器或ORM提供),构建偏好对(如“成功”轨迹 $\tau^{+}$ vs “失败”轨迹 $\tau^{-}$)。然后,使用一个类似DPO的目标函数来更新PRM $\pi_{\phi}$:
\[\mathcal{J}_{\text{PRM}}(\phi)=-\mathbb{E}_{(\tau^{+},\tau^{-})\sim\pi_{\theta_{\text{old}}}}\left[\log\sigma\left(\beta\log\frac{\pi_{\phi}(\tau^{+} \mid x)}{\pi_{\theta_{\text{old}}}(\tau^{+} \mid x)}-\beta\log\frac{\pi_{\phi}(\tau^{-} \mid x)}{\pi_{\theta_{\text{old}}}(\tau^{-} \mid x)}\right)\right]\]这个过程让PRM学会倾向于生成能带来更好结果的轨迹。
- 策略优化:使用更新后的PRM计算每个动作的隐式步骤奖励 $r_{\phi}$。然后,结合两种优势函数来更新策略 $\pi_{\theta}$:
-
情节级优势 (Episode-level Advantage) $A^{E}$:根据最终的结果奖励 $r_{o}(\tau)$ 计算,反映了整个轨迹的全局表现。
\[A^{E}(\tau_{i})=\big(r_{o}(\tau_{i})-mean(R_{o})\big)/std(R_{o})\] -
步骤级优势 (Step-level Advantage) $A^{S}$: 根据隐式步骤奖励 $r_{\phi}(a_t)$ 计算,反映了单个动作的局部贡献。
\[A^{S}(a_{t}^{i})=\left(r_{\phi}(a_{t}^{i})-mean(R_{s})\right)/std(R_{s})\] -
组合优势:将两种优势加权结合,为策略更新提供更全面的信号。
\[A(a_{t}^{i})=A^{E}(\tau_{i})+\alpha{A^{S}(a_{t}^{i})}\]最终,使用PPO等标准RL算法的代理目标函数进行策略更新。
-
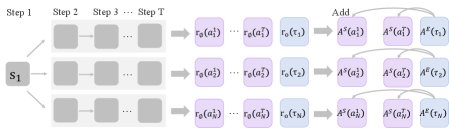
如上图所示,OPRL在更新策略时,最终的优势函数是情节级优势 $A^{E}(\tau)$ 和步骤级优势 $A^{S}(a)$ 的结合。
创新点
- 无标签的细粒度信誉分配:OPRL巧妙地通过DPO式的目标函数,将稀疏的、轨迹级别的结果偏好转化为稠密的、步骤级别的奖励信号,无需昂贵且有偏的人工步骤标签。
- 低方差与训练稳定性:通过在步骤(turn)级别而非 token 级别计算奖励,OPRL有效控制了奖励信号的粒度,避免了过细粒度信号带来的高方差问题。理论分析表明,其学习到的隐式步骤奖励是一种势能函数塑形奖励(potential-based reward shaping),能够保证最优策略不变,并提供有界的梯度,从而稳定了多轮次RL训练。
- 通用性与可扩展性:该方法仅依赖于轨迹级别的偏好,这些偏好可以来自基于规则的验证器(如任务成功信号),也可以来自LLM裁判等不可验证的ORM,使其能够统一应用于包括开放式对话在内的各类环境。同时,OPRL可与PPO、GRPO、RLOO等多种主流在线RL算法即插即用地结合。
理论分析
本文从理论上证明了OPRL的有效性与稳定性:
- 偏好一致性:在Bradley-Terry偏好模型假设下,最小化PRM损失函数等价于学习一个与潜在真实效用函数 $R^{\star}$ 一致的评分函数。
- 势能函数塑形:证明了累积的隐式步骤奖励 $\sum r_{\phi}$ 是对真实轨迹效用 $R^{\star}$ 的一种势能函数塑形,这种塑形不会改变原任务的最优策略集合。
- 梯度有界性:证明了策略梯度更新中的奖励项 $ \mid r_{\phi} \mid $ 是有界的,这保证了随机梯度优化的稳定性,使得PRM和策略的交替更新过程更加稳健。
实验结论
实验在三个具有挑战性的智能体基准上进行:WebShop(网页购物)、VisualSokoban(视觉推箱子)和SOTOPIA(开放式社交互动)。
主要性能
- 全面超越基准:在WebShop和VisualSokoban任务中,OPRL显著优于包括GPT-5、Gemini-2.5-Pro在内的前沿闭源模型,以及PPO、GRPO、PRIME、GiGPO等强RL基准。例如,在VisualSokoban上,成功率达到91.7%,远超其他方法。
| 方法 | WebShop (Qwen2.5-7B) | VisualSokoban (Qwen2.5-VL-7B) | |
|---|---|---|---|
| 成功率 | 分数 | 成功率 | |
| GPT-5 | 37.5 | 66.1 | 16.6 |
| Gemini-2.5-Pro | 30.5 | 38.4 | 16.0 |
| Base Model (ReAct) | 21.5 | 47.3 | 14.1 |
| + RLOO | 77.4 ± 1.1 | 87.6 ± 4.7 | 86.3 ± 0.6 |
| + PRIME | 81.5 ± 1.8 | 91.3 ± 0.6 | - |
| + GiGPO | 84.1 ± 3.9 | 91.2 ± 1.5 | 85.9 ± 2.6 |
| OPRL (本文) | 86.5 ± 2.8 | 93.6 ± 1.0 | 91.7 ± 1.2 |
- 在开放环境中表现出色:在状态空间开放且奖励不可验证的SOTOPIA环境中,OPRL同样表现优异。与基线相比,在困难场景中,OPRL在自对弈(Self-Chat)模式下将目标完成度提升了14%,在与GPT-4o对弈时提升了高达48%。
| 模型 / 方法 | 自对弈 | 与GPT-4o对弈 | ||
|---|---|---|---|---|
| 目标 (困难) | 目标 (全部) | 目标 (困难) | 目标 (全部) | |
| Qwen2.5-7B | ||||
| + GRPO | 6.97 | 8.31 | 6.42 | 7.84 |
| + OPRL (本文) | 7.11 | 8.42 | 6.76 | 8.36 |
| Llama3.1-8B | ||||
| + GRPO | 7.92 | 9.12 | 6.68 | 8.14 |
| + OPRL (本文) | 8.06 | 9.20 | 7.16 | 8.45 |
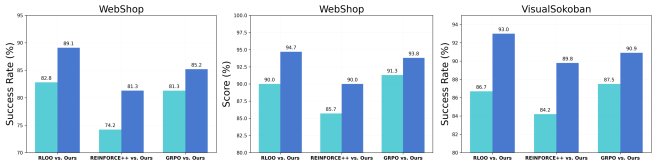
- 对不同RL算法的普适性:实验证明,OPRL能够稳定地提升包括RLOO、REINFORCE++和GRPO在内的多种不同RL算法的性能,展现了其强大的通用性和鲁棒性。
样本效率与训练稳定性
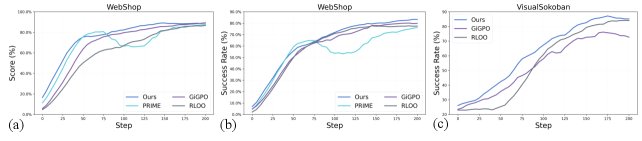
- OPRL展现了卓越的样本效率和训练稳定性。如上图所示,与基线相比,OPRL能够更快地收敛到更高的性能水平,并且训练过程中的性能曲线更平滑、波动更小。例如,在WebShop中,OPRL仅用105步就达到了基线RLOO方法的最终性能,训练效率提升约2倍。这验证了其步骤级奖励信号能有效降低梯度方差,实现更稳定的策略更新。
探索效率分析

- OPRL能够实现更高效的探索。如上图所示,在训练初期,隐式步骤奖励首先快速提升,随后带动了情节奖励的增长。这表明智能体首先学习到有效的局部动作启发,然后将它们组合成高回报的完整轨迹。同时,随着训练进行,智能体完成任务所需的平均步数显著减少,证明了OPRL能引导智能体减少不必要的动作,提升探索效率。
消融实验
消融实验验证了OPRL设计的关键性:
- 优势层面的融合至关重要:直接将步骤奖励和结果奖励相加(w/ merged rewards)的效果远不如在优势层面进行融合的OPRL。这表明,需要用最终结果来调节中间步骤的功劳,以防止智能体进行投机性的刷分行为。
- 步骤级奖励优于Token级奖励:使用token级别的过程奖励(w/ token-level PR)在长时程任务中表现次优,说明过于细粒度的奖励会引入噪声,增加策略学习的难度。
- 学习的奖励优于环境自带奖励:与使用VisualSokoban环境提供的真实步骤惩罚(w/ ground-truth PR)相比,OPRL学习到的隐式奖励能带来更大的性能提升,证明了其奖励信号的优越性。
| 方法消融 | WebShop | VisualSokoban | |
|---|---|---|---|
| 成功率 | 分数 | 成功率 | |
| RLOO (基线) | 76.6 | 84.2 | 85.9 |
| w/ ground-truth PR | - | - | 87.5 |
| w/ merged rewards | 81.3 | 90.7 | 88.3 |
| w/ token-level PR | 82.0 | 90.0 | 89.1 |
| OPRL | 86.5 | 93.6 | 91.7 |
综上,OPRL是一种高效、稳定且通用的信誉分配策略,在多种交互式环境中显著提升了LLM智能体的性能。