Opal: An Operator Algebra View of RLHF

• ArXiv URL: http://arxiv.org/abs/2509.11298v1

• 作者:

• 发布机构: Microsoft

---

TL;DR

本文提出了Opal，一个用于强化学习从人类反馈（RLHF）的算子代数视图，以及GKPO，一个标准化的交换模式，通过一个当且仅当满足三个核心假设时成立的约简定律，来统一、比较和验证不同的RLHF目标函数，从而整理了该领域繁杂的方法。

关键定义

本文提出或沿用了以下对理解其核心思想至关重要的概念：

1. 算子阶梯 (Ladder)：一种将RLHF目标函数形式化的表示方法，它被描述为一系列作用于基础效用函数（base score）\($u\)$上的原始算子序列。
2. 原始算子 (Primitive Operators)：构成“阶梯”的基本构建块，主要有两种：
   • 加性惩罚 (additive penalties) \($\mathcal{A}[\lambda, \phi]\)$：将效用函数\($f\)$平移，形式为 \($f \mapsto f - \lambda\phi\)$。
   • 乘性成对权重 (multiplicative pairwise weights) \($\mathcal{M}[\omega]\)$：缩放成对效用差（margin），形式为\($W \mapsto W \cdot \omega\)$。
   • 此外还包括一个参考调整 (reference adjustment) \($ \mathcal{R}[\Delta\_{\mathrm{ref}}]\)$。
3. 可约简类 (Reducible Class, $\mathcal{R}$)：指那些可以被无损地“折叠”或“约简”为一个统一范式（normal form）的算子阶梯所构成的集合。一个阶梯属于此类，当且仅当它满足三个条件：(1) 参考是固定的；(2) 惩罚是可加的；(3) 权重与中间效用差无关。
4. 范式 (Normal Form)：可约简阶梯的最终简化形式，其成对边际（pairwise margin）可以表示为 \($M = (\Delta f^{\ast} - \Delta\_{\mathrm{ref}}) w^{\ast}\)$，其中\($f^{\ast}\)$是所有加性惩罚的总和，\($w^{\ast}\)$是所有乘性权重的总积。
5. GKPO (通用核偏好对象, Generalized Kernel Preference Object)：一个规范化的JSON模式，用于表示任何成对的RLHF目标。对于可约简类中的方法，GKPO能将其规范化为Opal范式并生成确定性哈希；对于不可约简的方法，它会明确标记出失败的假设并提供“见证”（witness）。

相关工作

当前，从人类反馈中进行强化学习（RLHF）的领域充满了各种各样的方法，如PPO-RLHF、直接偏好优化（DPO, Direct Preference Optimization）、基于排序的方法（RRHF）、偏移正则化目标（ORPO）等，形成了一个庞杂的“方法动物园”。

这种方法的激增带来了一个根本性问题：这些看似不同的目标函数在本质上是真的不同，还是仅仅是同一基础算子的不同代数组合？这种混乱使得在不同方法之间进行公平比较、复现结果和理解其根本差异变得异常困难。

本文旨在解决这个问题，通过引入一个统一的算子代数框架（Opal）和一个标准化的表示模式（GKPO），来系统性地分类和比较现有的RLHF目标函数，阐明它们之间的等价关系或本质区别。

本文方法

本文的核心贡献是提出了一个名为Opal的算子代数框架，并基于此设计了GKPO，一个用于RLHF目标的标准化交换模式。

Opal：算子代数视图

Opal框架将RLHF目标建模为作用于基础效用对 \($(u, 1)\)$ 上的“算子阶梯”。一个阶梯 \($L\)$ 的规范化边际（canonical margin）定义为：

\[M_{L}(x;y^{+},y^{-}) = \bigl{(}\Delta f(x;y^{+},y^{-})-\Delta_{\mathrm{ref}}(x;y^{+},y^{-})\bigr{)}\cdot W(x,y^{+},y^{-})\]

其中，\($f\)$是变换后的效用，\($W\)$是成对权重，\($\Delta\_{\mathrm{ref}}\)$是参考调整。

原始算子与阶梯

阶梯由以下三种原始算子构成：

• 加性惩罚 \($\mathcal{A}[\lambda,\phi]\)$：通过 \($f \mapsto f-\lambda\phi\)$ 调整效用。
• 乘性权重 \($\mathcal{M}[\omega]\)$：通过 \($W \mapsto W\cdot\omega\)$ 调整权重。
• 参考调整 \($\mathcal{R}[\Delta\_{\mathrm{ref}}]\)$：直接修改参考项 \($\Delta\_{\mathrm{ref}}\)$。

由于加性算子和乘性算子分别满足交换律和结合律，任何阶梯都可以被表示为一个“收集后”的形式：

\[f = u-\sum_{i\in I}\lambda_{i}\phi_{i},\qquad W = \prod_{j\in J}\omega_{j}\]

创新点：可约简性与范式

本文最重要的理论贡献是提出了一个约简定律 (Reduction Law)：

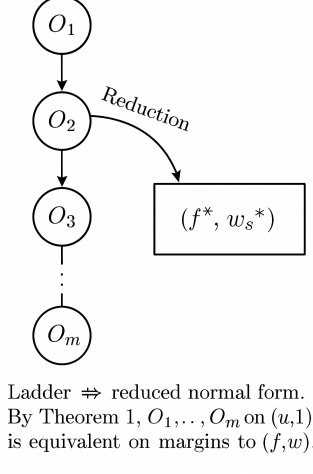
一个算子阶梯 \($L\)$ 可以被约简为一个范式 \($M\_{L} \equiv (\Delta f^{\ast}-\Delta\_{\mathrm{ref}}) w^{\ast}\)$，当且仅当以下三个假设成立：

1. 参考固定 (Fixed Reference)：\($\Delta\_{\mathrm{ref}}\)$ 在所有prompt之间是恒定的。
2. 惩罚可加 (Additive Penalties)：惩罚项可以线性叠加到效用函数 \($f\)$ 上。
3. 权重独立 (Score-independent Weights)：乘性权重 \($w\)$ 不依赖于中间的效用差值 \($\Delta f\)$。

当这些假设不成立时，该方法就变得不可约简 (non-reducibility)。本文为每种失败模式提供了明确的、有限的“见证”（witnesses），即具体的反例来证明其不可约简性：

• 参考偏移 (Reference shift)：当 \($\Delta\_{\mathrm{ref}}\)$ 随prompt变化时，不存在单个固定的范式能匹配所有决策。
• 非加性门控 (Non-additive gates)：当惩罚具有门控逻辑时（如 \($\mathbf{1}\{\phi\_1=0\}\phi\_2\)$），无法用一个非负的加性代理来表示。
• 效用依赖权重 (Score-dependent weights)：当权重是 \($\Delta f\)$ 的函数时，算子的应用顺序会改变最终决策，因此不存在一个与效用无关的 \($w^{\ast}\)$。

GKPO：一个标准化的交换模式

基于Opal的理论，本文设计了GKPO（通用核偏好对象），一个用于RLHF目标的具体、可执行的JSON模式。

优点

GKPO的设计具有以下核心优点：

1. 统一表示：GKPO为所有成对的RLHF目标提供了一个统一的、与方法无关的表示。这使得比较不同方法的配置变得简单直接。其JSON模式包括了效用、权重、参考、损失函数、惩罚项等关键组成部分。
2. 自动规范化与哈希：
   • 对于满足可约简条件的RLHF方法，GKPO可以自动将其规范化 (Canonicalization)为Opal范式。
   • 通过对规范化后的JSON进行确定性序列化和SHA-256哈希，生成一个Opal哈希 (Opal hash)。这个哈希值对于所有代数等价的目标函数都是唯一的，为方法的复现和验证提供了强有力的工具。
3. 明确的失败诊断：当一个方法不可约简时，GKPO不会尝试强行转换。相反，它会在 \(reducibility\) 字段中明确标记 \(inside_R: false\)，并指出失败的原因（如 \(reference_shift\)），同时提供一个最小的“见证”（witness）来证明这一点。这使得方法的根本假设和局限性变得透明。
4. 方法间转换器：GKPO充当了方法间的“交换层”。只要方法是可约简的，就可以通过 \($X \to \text{GKPO} \to Y\)$ 的路径实现方法间的转换，同时保持其边际和决策不变（在正向缩放范围内）。

GKPO 示例

一个DPO方法的极简GKPO实例如下： ``\(json { "version": "gkpo-1.0", "score": { "type": "logpi" }, "weight": { "form": "constant", "constant": 1.0 }, "reference": { "form": "fixed_scalar", "value": 0.10 }, "link": "identity", "loss": "logistic", "beta": 1.0, "penalties": [], "provenance": { "method": "DPO", "citations": ["rafailov2023direct"] }, "reducibility": { "inside_R": true, "reasons": [], "witness": {} } }\)`$$

实验结论

本文没有进行大规模的基准测试，而是通过一系列精心设计的“演示”和“压力测试”来验证Opal代数和GKPO模式的有效性。

• 可行性验证：通过具体的玩具样本（Toy Examples），成功地将DPO、RRHF等主流方法表示为GKPO实例。例如，将RRHF的排序惩罚表示为GKPO中的 \(penalties\) 项，展示了其在可约简类中的表达能力。
• 等价性验证：演示了在满足可约简假设的情况下，不同方法间的转换是可行的。例如，在固定参考和加性惩罚的条件下，RRHF可以被约简为与DPO等价的范式。同样，PPO-RM（带固定参考）也被证明可以约简为DPO形式，GKPO使得这种等价关系变得明确。
• 不可约简性验证：通过三个“压力测试”（SHIFT/GATE/SCORE）清晰地展示了三种失败模式：
  • SHIFT (参考偏移)：构造了两个具有相同原始效用差但不同参考偏移的prompt，导致最终的边际符号相反，证明了固定范式无法同时匹配两者。
  • GATE (非加性门控)：构造了一个门控惩罚的例子，证明无法找到一个等效的非负加性代理。
  • SCORE (效用依赖权重)：展示了当权重依赖于效用差时，算子应用顺序会改变最终决策的符号，从而证明了其不可约简性。

最终结论：这些演示和测试有力地支持了本文的核心论点。Opal框架和GKPO模式能够有效地对现有的RLHF方法进行分类、比较和转换。对于可约简的方法，GKPO能揭示它们的代数等价性；对于不可约简的方法，它能清晰地指出其核心假设的破坏点，为理解和复现RLHF研究提供了极大的清晰度和严谨性。

下表总结了Opal视角下的方法分类：

方法	可约简性	GKPO表示中的关键差异 (Delta)
PPO-RM	依赖	KL锚点作为\($f\)$上的加性惩罚。若参考固定则可约简。
DPO	是	范式本身。\($f=u, w=1\)$，参考为\($\log \pi\_{\text{ref}}\)$。
RRHF	依赖	排序惩罚作为\($f\)$上的加性惩罚。若惩罚线性则可约简。
ORPO	依赖	偏移量作为参考项\($\Delta\_{\text{ref}}\)$。若参考固定则可约简。
KTO / GRPO	依赖	方差塑造项可作为乘性权重\($w\)$。若\($w\)$与\($\Delta f\)$无关则可约简。
f-DPO / VAR	否	参考项$$$\Delta_{\text{ref}}$`随prompt变化（参考偏移）。
RLAIF / CAI	依赖	数据集级算子。若为加性/乘性则可约简。