Outcome-based Exploration for LLM Reasoning

• ArXiv URL: http://arxiv.org/abs/2509.06941v1

• 作者: Yuda Song; Julia Kempe

• 发布机构: CMU; Meta; NYU

---

TL;DR

本文提出了一种“基于结果的探索”（Outcome-based Exploration）方法，通过在强化学习训练中根据最终答案（而非整个推理过程）给予探索奖励，有效提升了大型语言模型在推理任务上的准确率，同时缓解了传统RL训练导致的生成多样性下降问题。

关键定义

• 基于结果的探索 (Outcome-based Exploration)：一种强化学习探索策略，其核心思想是探索奖励（bonus）仅依赖于生成内容的最终结果（如数学题的答案），而不是整个高维度的推理路径（token序列）。这种方法利用了推理任务中“结果空间”远小于“推理空间”的特性，使得探索变得高效且易于处理。
• 多样性退化的传递 (Transfer of Diversity Degradation)：本文发现的一种现象。当强化学习使模型在已解决的问题上收敛于少数正确答案时，这种多样性的损失会“传递”到尚未解决的问题上，导致模型在这些问题上的探索能力也随之下降，从而陷入局部最优。
• 结果空间的可处理性 (Tractability of the Outcome Space)：指在可验证的推理任务（如数学竞赛）中，尽管可能的推理路径（reasoning traces）数量巨大，但不同路径最终导向的有效答案数量相对有限且可管理。这是“基于结果的探索”方法可行性的关键前提。
• 历史探索 (Historical Exploration)：一种基于结果的探索算法，旨在鼓励模型在整个训练历史中访问更多样化的答案。它通过给予历史上罕见的答案以UCB（Upper Confidence Bound）式的奖励，来提升训练过程中的探索效率，主要目标是提升\(pass@1\)准确率。
• 批次探索 (Batch Exploration)：另一种基于结果的探索算法，旨在提升模型在测试时的生成多样性。它通过惩罚在当前生成批次（batch）内重复出现的答案，来直接激励模型产出多样化的输出，主要目标是改善高\(k\)值下的\(pass@k\)表现。

相关工作

当前，使用强化学习（RL）对大型语言模型（LLM）进行后训练（post-training）是提升其推理能力的主流方法。基于结果的强化学习，即只根据最终答案的正确性给予奖励，已被证明能显著提高模型准确率。

然而，这种方法存在一个严重的瓶颈：系统性的多样性丧失。经过RL训练后，模型生成的答案多样性会急剧下降，这体现在\(pass@k\)指标上——当\(k\)值较大时，RL后的模型表现甚至不如基础模型。这种多样性崩溃会损害模型在实际应用中的扩展能力，因为在测试时通过多次采样或树搜索等方法来提升性能依赖于生成的多样性。

本文旨在解决的核心问题是：如何在通过强化学习提升LLM推理准确率的同时，避免或缓解生成多样性的严重下降，从而实现准确性与多样性之间的更优平衡。

本文方法

本文的核心创新在于提出了“基于结果的探索”框架，将探索的焦点从难以处理的推理路径空间转移到可管理的最终答案空间。

RL作为采样过程的视角与动机

本文首先将RL训练过程视为一个在训练集上的采样过程，并与直接从基础模型采样进行对比。通过实验观察到两个关键现象，这构成了本文方法的动机：

1. 多样性退化的传递：RL在已解决的问题上强化正确答案，导致概率分布坍塌。这种多样性的降低会泛化到未解决的问题上，使得模型在这些问题上探索新答案的能力也下降。如下图所示，RL（实线）在未解决问题上发现的新答案数量（虚线）甚至低于基础模型采样。
2. 结果空间的可处理性：在数学推理等任务中，尽管推理过程千变万化，但最终的答案种类是有限的（通常少于50种）。这使得基于答案的计数和探索成为可能。

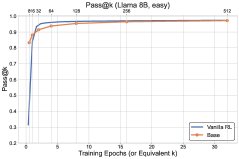
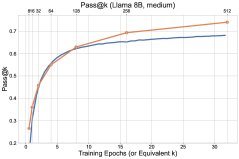
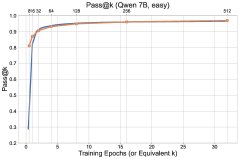
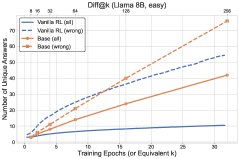
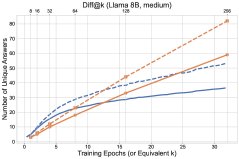
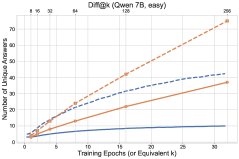
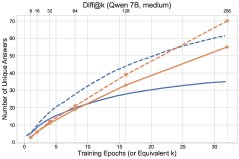
图2: RL训练动态与基础模型采样的对比。顶部：已解决问题数；底部：发现的不同答案数。实线代表所有问题，虚线代表未解决问题。

历史探索 (\(Historical Exploration\))

为了解决多样性下降问题，本文首先引入了基于历史计数的探索方法，类似于经典的UCB算法。在RL的目标函数中加入一项探索奖励：

\[\widehat{\operatorname{\mathbb{E}}}\_{x,\{y\_{i},a\_{i}\}\_{i=1}^{n}\sim\pi(\cdot\mid x)}\left[\frac{1}{n}\sum\_{i=1}^{n}\widehat{A}\left(x,\{y\_{i},a\_{i}\}\_{i=1}^{n}\right)\_{i}+cb\_{\mathsf{ucb}}(x,a\_{i})-\beta\widehat{\mathrm{KL}}(\pi(\cdot\mid x),\pi\_{\mathsf{base}}(\cdot\mid x))\right],\]

其中探索奖励 $b_{\mathsf{ucb}}(x,a)=\min\left{1,\sqrt{\frac{1}{N(x,a)}}\right}$，$N(x,a)$ 是答案 $a$ 对问题 $x$ 历史出现的次数。

• 朴素UCB的问题：实验发现，直接使用上述UCB奖励（称为朴素UCB）虽然能提升训练期的探索效率（更快解决更多问题），但对测试性能的提升不稳定。这可能是因为它会鼓励模型重复访问已知的错误答案，从而损害泛化能力。

• 带基线的UCB (\(UCB-Mean\) & \(UCB-Con\))：为了解决此问题，本文提出在探索奖励中引入基线（baseline），从而可以施加“负向探索”信号（即惩罚）。

  • \(UCB-Mean\)：使用当前批次内UCB奖励的均值作为基线。这鼓励模型探索在当前批次内相对罕见的答案。
  • \(UCB-Con\)：使用一个固定的常数 $b_0$ 作为基线，奖励项变为 $b_{\mathsf{ucb}}(x,a_{i})-b_{0}$。这使得访问次数过多的答案会受到惩罚。例如，当 $b_0=0.5$ 时，被访问超过4次的答案会获得负奖励。实验证明，\(UCB-Con\) 在所有方法中表现最好，能持续提升测试性能。

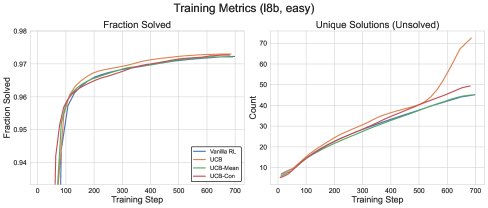
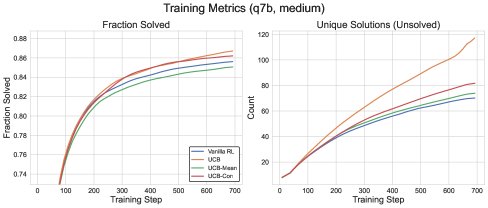图3: 不同UCB变体与GRPO基线的训练性能对比。

图4: 不同UCB变体与GRPO基线的测试性能对比。

批次探索 (\(Batch Exploration\))

历史探索旨在找到最优解（优化\(pass@1\)），但未必能保证测试时生成的多样性。为了直接优化测试时的多样性（高\(k\)值的\(pass@k\)），本文提出了批次探索。其奖励机制替换为：

\[b\_{\mathsf{batch}}\left(x,\{y\_{i},a\_{i}\}\_{i=1}^{n}\right)\_{i}=-\frac{1}{n}\sum\_{j\neq i}\mathbf{1}\{a\_{i}=a\_{j}\}\]

这个奖励直接惩罚在当前批次内重复出现的答案，从而激励模型为同一问题生成更多样化的答案。

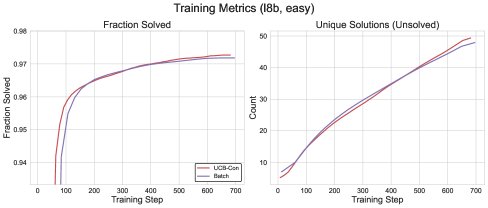
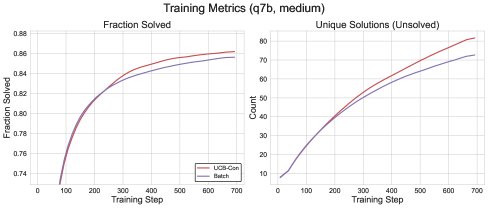图5: \(Batch\)与\(UCB-Con\)方法的训练性能对比。

理论分析：基于结果的赌博机

为了从理论上支撑“基于结果的探索”的合理性，本文提出了一个名为“基于结果的赌博机”（Outcome-Based Bandits）的新模型。该模型抽象了LLM的推理过程：有 $K$ 个臂（代表推理路径），但只有 $m$ 个结果（代表最终答案），其中 $m \ll K$。

• 定理4.1 (非正式) 表明，如果没有额外的泛化假设，仅仅利用结果进行划分并不能降低问题的复杂度，其遗憾下界仍与臂的数量 $K$ 相关。
• 定理4.2 (非正式) 则证明，如果做出一个合理的泛化假设（即对一个推理路径的更新能影响到产生相同答案的其他路径），那么采用基于结果的UCB式探索算法，其遗憾上界仅与结果数量 $m$ 相关，即 $O\left(\sqrt{mT\log T}\right)$。这从理论上说明了本文方法的样本高效性。

实验结论

本文在\(Llama\)和\(Qwen\)系列模型上，使用\(MATH\)和\(DAPO\)等数学推理数据集进行了广泛实验。

核心实验对比

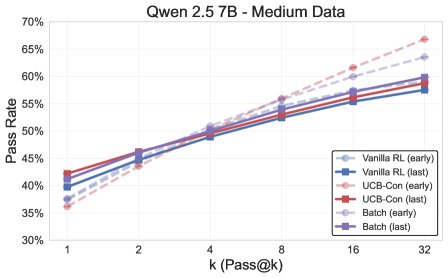图1: 最终实验结果概览，探索方法（\(UCB-Con\)和\(Batch\)）在\(pass@k\)指标上全面优于基线\(GRPO\)。

• 探索方法全面超越基线：所有提出的探索方法（\(UCB-Mean\)、\(UCB-Con\)、\(Batch\)）在测试集上的\(pass@k\)（对于$k \in {1, …, 32}$）几乎都优于标准的RL基线（\(GRPO\)）。
• \(UCB-Con\)是最佳性能提升者：在历史探索的变体中，\(UCB-Con\)（带常数基线）表现最佳，它在所有\(k\)值上都能稳定地提升性能，并有效缓解了标准RL后期出现的过优化问题（即性能下降）。
• \(Batch\)在多样性-准确性权衡上更优：批次探索（\(Batch\)）虽然在训练过程中的探索效率不如\(UCB-Con\)，但在测试时能产生更多样的答案。因此，在训练后期，它在高\(k\)值的\(pass@k\)上表现突出，实现了更好的准确性-多样性权衡，特别适合以测试时扩展性为目标的场景。

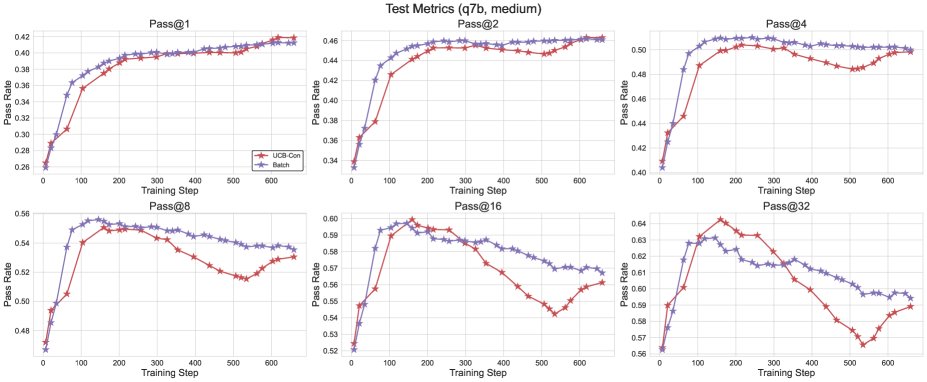图6: \(Batch\)与\(UCB-Con\)方法的测试性能对比，\(Batch\)在训练后期的大\(k\)值\(pass@k\)上显示出优势。

补充分析

• 生成熵：\(Batch\)方法在生成错误答案时的token级熵显著高于\(GRPO\)和\(UCB-Con\)，表明其生成的内容本身更具变化性。

	正确生成	错误生成	所有
\(GRPO\)	0.080 (0.01)	0.096 (0.04)	0.095 (0.02)
\(UCB-Con\)	0.084 (0.01)	0.103 (0.03)	0.100 (0.02)
\(Batch\)	0.086 (0.01)	0.153 (0.07)	0.125 (0.03)

表1: 不同方法生成内容的熵对比。

• 批次内多样性：\(Batch\)方法在每个批次内生成的不同答案数量也显著多于其他方法，这与它的设计目标完全一致。

	已解决问题	未解决问题	所有
\(GRPO\)	2.279 (0.018)	4.805 (0.075)	2.883 (0.024)
\(UCB-Con\)	2.272 (0.020)	4.855 (0.084)	2.926 (0.035)
\(Batch\)	2.284 (0.057)	5.390 (0.102)	3.230 (0.062)

表2: 批次内生成不同答案数量的对比。

总结

本文证实，基于结果的探索是解决RL训练中多样性下降问题的有效途径。历史探索（特别是\(UCB-Con\)）能显著提高整体推理准确性，而批次探索（\(Batch\)）则在保证准确性的同时，最大化了测试时的生成多样性。这两种方法是互补的，为训练既准确又多样化的LLM推理智能体指明了实用可行的方向。