Parameter-Efficient Fine-Tuning for Large Models: A Comprehensive Survey
-
ArXiv URL: http://arxiv.org/abs/2403.14608v7
-
作者: Jeff Zhang; Sai Qian Zhang; Chao Gao; Jinyang Liu; Zeyu Han
-
发布机构: Arizona State University; New York University; Northeastern University; University of California, Riverside
引言
大型模型 (Large Models, LMs) 在自然语言处理 (NLP) 和计算机视觉 (CV) 等多个领域取得了显著进展,但其巨大的规模带来了高昂的计算成本。参数高效微调 (Parameter-Efficient Fine-Tuning, PEFT) 通过在冻结大部分预训练模型参数的同时,仅调整一小部分参数,为将大模型适配到下游特定任务提供了可行的解决方案。本文系统性地回顾和分类了近年来的PEFT算法,探讨了它们在不同场景下的性能、计算开销和系统实现成本,旨在为研究人员提供关于PEFT算法和系统实现的全面概览。

图1: 本综述覆盖的内容概览。
背景知识
LLaMA的计算流程
为了理解大模型,本文以LLaMA-7B为例,剖析了其架构和计算流程。LLaMA模型主要由三部分组成:一个嵌入层 (embedding block)、一个解码器栈 (stack of decoder blocks) 和一个输出头 (head block)。
每个解码器包含两个核心组件:多头自注意力 (Multi-head Self-Attention, MSA) 和前馈网络 (Feedforward Network, FFN)。LLM的计算具有自回归 (autoregressive) 的特性,即逐个Token生成,同时其注意力机制的计算复杂度与输入序列长度成二次方关系。
在推理过程中,解码器的输入为张量 $x\in\mathbb{R}^{b\times l\times d}$。首先通过与权重矩阵 $W_{Q}, W_{K}, W_{V}$ 相乘得到查询 (Query, $Q$)、键 (Key, $K$) 和值 (Value, $V$)。LLaMA使用旋转位置编码 (Rotary Positional Embedding, RoPE) 来注入位置信息。注意力计算过程如下:
\[Q,K,V=R(W_{q}x),R(W_{k}x),W_{v}x\] \[SA(x)=Softmax(\frac{QK^{T}}{\sqrt{d_{head}}})V\] \[MSA(x)=[SA_{1}(x);SA_{2}(x);\ldots;SA_{k}(x)]W_{o}\]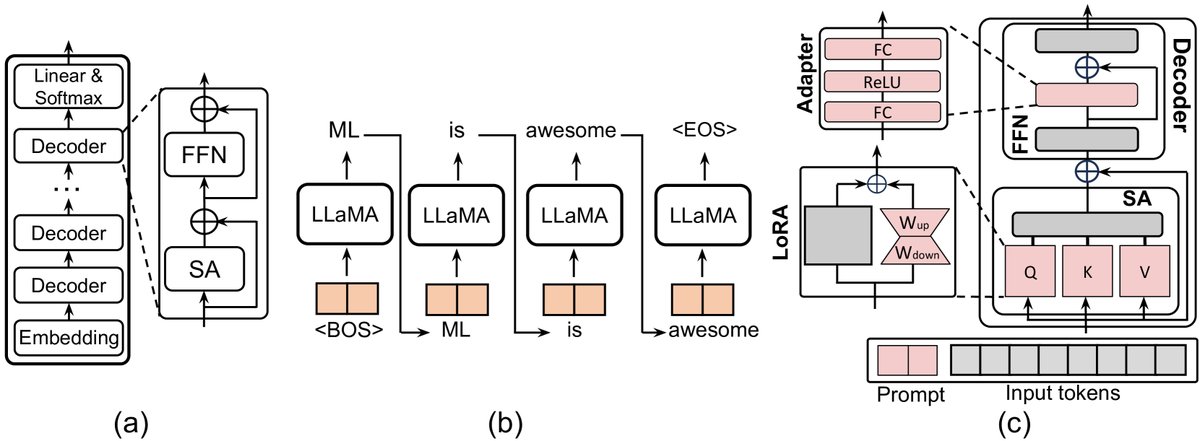
图2: (a) LLaMA架构。(b) LLaMA自回归模式。(c) 三种常见的PEFT操作。可学习组件为红色,冻结组件为灰色。
随后,输出进入FFN模块。LLaMA中的FFN计算如下,其中 $SiLU$ 为激活函数:
\[FFN\_{LLaMa}(x)=W\_{up}(SiLU(W\_{gate}x)\odot(W\_{down}x))+x\]而原始Transformer的FFN为:
\[FFN\_{Transfomer}(x)=W\_{up}(ReLU(W\_{down}x))+x\]为了加速推理,通常使用键值缓存 (Key-Value cache, KV-cache) 来存储先前所有Token的 $K$ 和 $V$ 值。其内存成本可表示为:
\[Size=L\times 2\times b\times l\times d\_{head}\times n\_{head}\]其中 $L$ 是层数,$b$ 是批量大小,$l$ 是上下文长度,$d_{head}$ 是注意力头的维度,$n_{head}$ 是头的数量。
表 I: LLaMA-7B架构的配置和计算操作
| 操作 | 权重符号 | 权重维度 | 输入张量维度 | 复杂度 |
|---|---|---|---|---|
| 方程 (1) | $W_{Q}$, $W_{K}$, $W_{V}$ | $d\times k\times\frac{d}{k}$ | $b\times l\times d$ | $O(l)$ |
| 方程 (2) | - | - | $b\times l\times 3\times k\times\frac{d}{k}$ | $O(l^{2})$ |
| 方程 (3) | $W_{o}$ | $d\times d$ | $b\times l\times d$ | $O(l)$ |
| 方程 (4) | $W_{up}$, $W_{down}$, $W_{gate}$ | $d\times 4d$ | $b\times l\times d$ OR $l\times b\times 4d$ | $O(l)$ |
参数高效微调概览
随着模型规模的增长,全量微调变得极其低效和昂贵。PEFT旨在通过仅微调极少数参数来在下游任务上达到甚至超过全量微调的性能。本文将PEFT方法分为四类:
- 加性微调 (Additive Fine-tuning):在模型中添加新的可训练模块或参数。
- 选择性微调 (Selective Fine-tuning):选择模型现有参数的一个子集进行微调。
- 重参数化微调 (Reparameterized Fine-tuning):在训练时引入额外的低秩可训练参数,在推理时将其与原始模型参数合并。
- 混合微调 (Hybrid Fine-tuning):结合不同PEFT方法的优点。
下游任务与评估基准
下游任务:
- NLP: 通用语言理解评估 (General Language Understanding Evaluation, GLUE) 基准和一系列常识推理任务,如OpenBookQA, PIQA, Social IQA等。
- CV:
- 图像识别:如细粒度视觉分类 (FGVC)和视觉任务自适应基准 (VTAB)。
- 视频动作识别:如Kinetics-400, SSv2, HMDB51。
- 密集预测:如MSCOCO, ADE20K, PASCAL VOC。
评估基准:
- 算法视角: [25], [26], [27] 等工作在大量NLP任务上对不同PEFT算法的性能、效率、可扩展性等进行了基准测试。
- 系统视角:
- ShareGPT数据集 [28]: 包含真实的用户与ChatGPT的交互,用于评估系统处理多样化对话需求的能力。
- 微软Azure函数追踪 [29]: 用于模拟LLM系统可能面临的请求到达模式和工作负载强度。
- Gamma过程 [30]: 一种模拟排队系统中请求到达时间的随机过程,用于生成合成但真实的负载场景,以在受控条件下测试系统性能。
PEFT分类体系
本文将PEFT策略分为四大类:加性PEFT、选择性PEFT、重参数化PEFT和混合PEFT。
$$ [ PEFT Methods for PLMs, ver [ Additive Fine-tuning [ Adapter-based Fine-tuning [ Adapter Design [ Serial Adapter [31], Parallel Adapter [32], CIAT [33], CoDA [34] ] ] [ Multi-task Adaptation [ AdapterFusion [35], AdaMix [36], PHA [37], AdapterSoup [38], MerA [39], Hyperformer [40] ] ] ] [ Soft Prompt-based Fine-tuning [ Soft Prompt Design [ Prefix-tuning [41], Prefix-Propagation [42], p-tuning v2 [43], APT [44], p-tuning [45], prompt-tuning [46], Xprompt [47], IDPG [48], LPT [49], SPT [50], APrompt [51] ] ] [ Training Speedup [ SPoT [52], TPT [53], InfoPrompt [54], PTP [55], IPT [56], SMoP [57], DePT [58] ] ] ] [ Others [ (IA)^3 [59], MoV [60], SSF [61], IPA [62] ] ] ] [ Selective Fine-tuning [ Unstructural Masking [ U-Diff pruning [63], U-BitFit [64], PaFi [65], FishMask [66], Fish-Dip [67], LT-SFT [68], SAM [69], Child-tuning [70] ] ] [ Structural Masking [ S-Diff pruning [63], S-BitFit [64], FAR [71], Bitfit [72], Xattn Tuning [73], SPT [74] ] ] ] [ Reparameterized Fine-tuning [ Low-rank Decomposition [ Intrinsic SAID [75], LoRA [76], Compacter [77], KronA [78], KAdaptation [79], HiWi [65], VeRA [80], DoRA [81] ] ] [ LoRA Derivatives [ Dynamic Rank [ DyLoRA [82], AdaLoRA [83], SoRA [84], CapaBoost [85], AutoLoRA [86] ] ] [ LoRA Improvement [ Laplace-LoRA [87], LoRA Dropout [88], PeriodicLoRA [89], LoRA+ [90], MoSLoRA [91] ] ] [ Multiple LoRA [ LoRAHub [92], MOELoRA [93], MoLORA [60], MoA [94], MoLE [95], MixLoRA [96] ] ] ] ] [ Hybrid Fine-tuning [ UniPELT [97], S4 [98], MAM Adapter [32], NOAH [99], AUTOPEFT [100], LLM-Adapters [101], S^3PET [102] ] ] ] $$
图3: 大模型参数高效微调方法的分类体系。
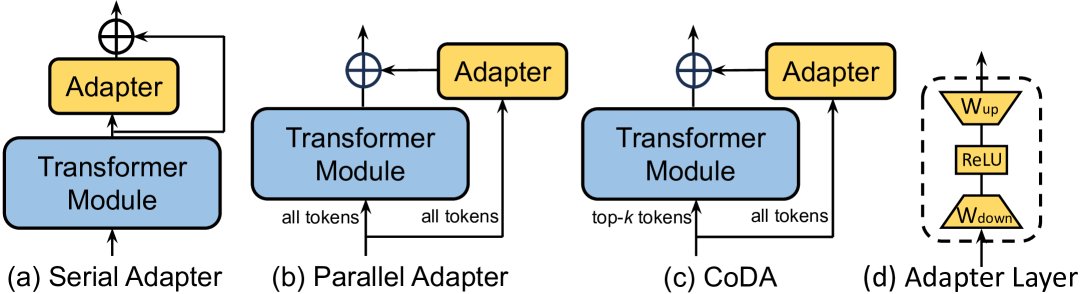
图4: 不同类型的PEFT算法。
加性PEFT
加性PEFT的核心思想是保持预训练模型的主体参数不变,通过在模型架构中(如图4(a)所示)策略性地插入少量新的可训练模块或参数来进行微调。
适配器 (Adapters)
适配器方法在Transformer模块内部插入小型的“适配器层”。一个典型的适配器层包含一个降维投影矩阵 $W_{\text{down}}\in\mathbb{R}^{r\times d}$、一个非线性激活函数 $\sigma(\cdot)$ 和一个升维投影矩阵 $W_{\text{up}}\in\mathbb{R}^{d\times r}$,其中 $r$ 是远小于 $d$ 的瓶颈维度。其计算如下:
\[Adapter(x)=W\_{\text{up}}\sigma(W\_{\text{down}}x)+x\]- 设计: 早期工作如Serial Adapter [31] 将适配器串行插入(图5(a))。为减少推理延迟,后续工作提出了并行适配器(Parallel Adapter, PA)[32](图5(b)),将适配器作为一个旁路网络。CoDA [34] 则在并行适配器的基础上引入稀疏激活机制,仅让重要Token通过主干网络,以提升效率(图5(c))。
- 多任务学习: 为提升适配器的性能和泛化能力,发展出了多种多任务学习策略,如AdapterFusion [35]、AdaMix [36]、MerA [39] 和 Hyperformer [40] 等,它们通过融合、合并或动态生成适配器参数来整合多任务信息。
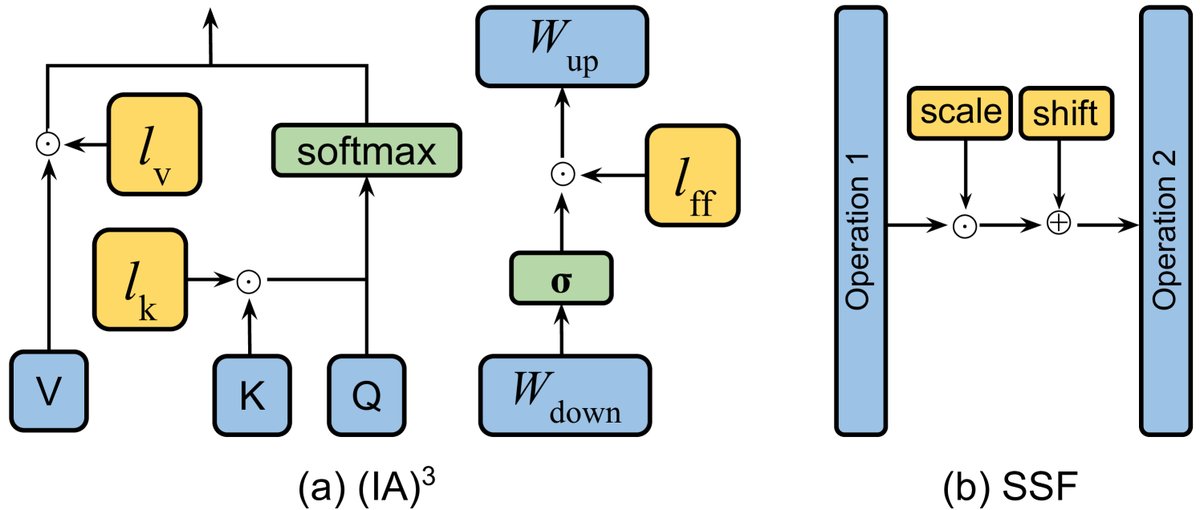
图5: 三种代表性的基于适配器的微调算法图示。蓝色代表冻结,黄色代表可训练。
软提示 (Soft Prompt)
提示微调 (Prompt Tuning) 是另一种方法,它不是调整模型权重,而是在输入序列前添加可学习的连续向量,即“软提示”。其形式为:
\[\mathbf{X}^{(l)}=[\mathbf{s}\_{1}^{(l)},\ldots,\mathbf{s}\_{N\_{S}}^{(l)},\mathbf{x}\_{1}^{(l)},\ldots,\mathbf{x}\_{N\_{X}}^{(l)}]\]其中 $\mathbf{s}_{i}^{(l)}$ 是软提示Token。
- 设计:
- Prefix-tuning [41] 在Transformer的每一层都为键(Key)和值(Value)添加可学习的前缀向量。
- p-tuning [45] 和 prompt-tuning [46] 仅在输入嵌入层添加软提示,以提升效率。Prompt-tuning在超大模型(>11B)上效果显著。
- LPT [49] 和 SPT [50] 探索了更优的提示插入策略,如在中间层插入或通过门控机制选择性插入,以加速训练并提升性能。
- 训练加速: 为解决软提示训练不稳定的问题,研究者们提出了多种策略,如使用源任务提示初始化新任务的SPoT [52],引入正则化项平滑损失函数的PTP [55],以及将长提示分解为短提示和低秩矩阵的DePT [58]等。
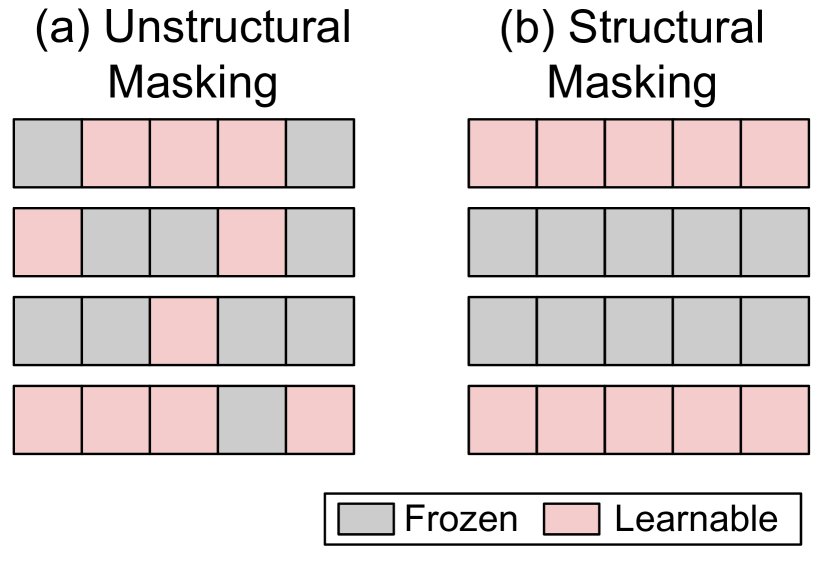
图6: (IA)³ 和 SSF 的图示。蓝色代表冻结,黄色代表可训练。
其他加性方法
除了适配器和软提示,还有其他方法通过添加少量参数进行微调。
-
(IA)³ [59] (Infused Adapter by reparameterizing Attention and FFN) 引入三个可学习的缩放向量 $l_{k}, l_{v}, l_{ff}$,分别对注意力中的键、值以及FFN的激活进行逐元素缩放(见图6(a))。计算示例如下:
\[SA(x)=Softmax(\frac{Q(l\_{k}\odot K^{T})}{\sqrt{d\_{head}}})((l\_{v}\odot V)\] \[FFN\_{Transfomer}(x)=W\_{\text{up}}(l\_{\text{ff}}\odot\sigma(W\_{down}x))\]这些缩放向量在推理时可以被合并到模型的权重矩阵中,因此不引入额外的计算开销。
- SSF [61] (Scaling and Shifting Features) 在模型的每个操作(如MSA, FFN)后插入一个包含可学习的缩放和偏移参数的层(见图6(b))。与(IA)³类似,这些参数也可以在推理时合并,实现无损推理效率。
- IPA [62] (Inference-Time Policy Adapters) 在解码阶段,通过组合一个小型“适配器策略”模型和一个大型基础模型的输出分布,来对齐大模型(如GPT-4)的行为,而无需修改基础模型参数。
选择性PEFT
选择性PEFT不增加新参数,而是选择模型现有参数的一个子集进行微调(如图4(b)所示)。这可以通过一个二进制掩码 $M$ 来实现,只有当掩码 $m_i=1$ 时,对应的参数 $\theta_i$ 才会被更新。
\[\theta^{\prime}\_{i}=\theta\_{i}-\eta\cdot m\_{i}\cdot\frac{\partial\mathcal{L}}{\partial\theta\_{i}}\]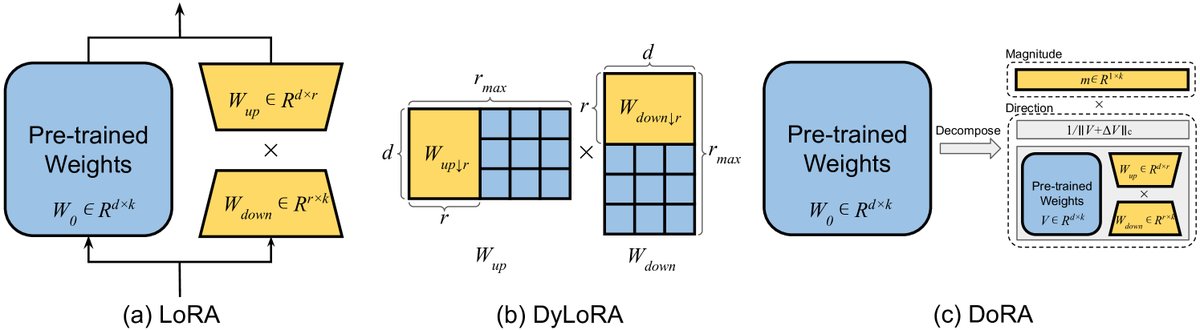
图7: 两种参数掩码方法的图示。
根据掩码的模式,可分为两类:
- 非结构化掩码 (Unstructural Masking):掩码的分布是稀疏且不规则的(如图7左),这可能导致硬件效率低下。
- Diff pruning [63] 使用可学习的二进制掩码,并用 $L_0$ 范数正则化来控制稀疏度。
- FishMask [66] 和 Fish-Dip [67] 利用费雪信息 (Fisher information) 来评估参数的重要性,从而选择要微调的参数子集。
- Child-tuning [70] 在每次训练迭代中选择一个“子网络”,并只更新该子网络内的参数。
- 结构化掩码 (Structural Masking):掩码以规则的模式组织,如按层、按块或按特定类型的参数进行选择(如图7右),从而提高计算和硬件效率。
- Bitfit [72] 是一种极简方法,仅微调模型中所有层的偏置 (bias) 参数。
- FAR [71] 对FFN中的权重进行分组,并根据 $L_1$ 范数选择“学习节点”进行微调。
- SPT [74]首先通过一轮前向和反向传播计算参数的敏感度,然后选择包含较多敏感参数的权重矩阵,并对这些矩阵应用PEFT方法(如LoRA),实现结构化微调。
重参数化PEFT
重参数化 (Reparameterization) 指的是通过参数变换将一个模型架构等价地转换为另一个。在PEFT的背景下,这通常意味着在训练阶段构建一个低秩的参数化表示以实现参数效率。在推理阶段,这个低秩表示可以被重新转换并合并回原始模型的权重参数中,从而保证推理速度不受影响。