Predicting Task Performance with Context-aware Scaling Laws
-
ArXiv URL: http://arxiv.org/abs/2510.14919v1
-
作者: Chenguang Wang; Michael Bendersky; David Park; Beliz Gunel; Dawn Song; Kyle Montgomery; Jianhong Tu
-
发布机构: Databricks; Google DeepMind; University of California, Berkeley; University of California, Santa Cruz; Washington University in St. Louis
TL;DR
本文提出了一个简洁、可解释的上下文感知缩放定律 (context-aware scaling law) 框架,该框架通过一个函数联合建模了训练计算量和上下文长度,从而能够准确预测和推断大型语言模型在下游任务中的性能。
关键定义
本文的核心是提出了一个新的缩放定律函数形式,并沿用了以下关键领域术语:
- 训练计算量 (Training Compute, $C$): 指用于训练模型的总计算资源,通常以 FLOPs (浮点运算次数) 衡量。本文遵循 Kaplan 等人的估算方法,即 $C \approx 6ND$,其中 $N$ 是模型参数量,$D$ 是训练数据集的Token数量。
- 上下文长度 (Context Length, $n_{\text{pmt}}$): 指在推理时提供给模型的输入查询或上下文的长度(以Token计)。
- 上下文限制 (Context Limit, $n_{\text{ctx}}$): 指模型在训练期间所能处理的最大序列长度(以Token计),即位置编码的最大数量。
-
上下文感知缩放定律 (Context-aware Scaling Law): 本文提出的核心公式,用于预测下游任务性能 $\mathcal{P}$。它是一个关于训练计算量 $C$、上下文长度 $n_{\text{pmt}}$ 和上下文限制 $n_{\text{ctx}}$ 的函数,其形式如下:
\[\begin{aligned} \mathcal{P}(C, n_{\text{pmt}}, n_{\text{ctx}}) &= \overbrace{\Biggl[1 - \exp\Biggl(-A \left(\frac{C}{C^{c}}\right)^{\alpha}\Biggr)\Biggr]}^{\text{关于 }C\text{ 的饱和项}} \\ &\times \underbrace{\Biggl[1 - \exp\Biggl(-B \left(\frac{n_{\text{pmt}}}{n_{\text{pmt}}^{c}}\right)^{\beta}\Biggr)\Biggr]}_{\text{关于 }n_{\text{pmt}}\text{ 的饱和项}} \\ &\times \underbrace{\sigma(n_{\text{pmt}} - n_{\text{ctx}})}_{\text{惩罚项}} \end{aligned}\]其中 $A, C^{c}, \alpha, B, n_{\text{pmt}}^{c}, \beta$ 是需要优化的参数,$\sigma$ 是一个 sigmoid 惩罚函数。
相关工作
传统的神经缩放定律 (neural scaling laws) 已经成功地揭示了上游指标(如交叉熵损失)与模型规模、数据量和计算量之间的关系,极大地指导了大型语言模型(LLMs)的设计。然而,这些定律存在一个关键瓶颈:它们通常无法准确预测模型在下游实际应用任务中的性能,因为下游任务性能不仅受模型本身能力的影响,还严重依赖于推理时提供的上下文 (context)。
现有的一些预测下游性能的工作,要么方法过于复杂、可解释性差(例如,使用多层感知机或依赖上游损失作为中间媒介的两阶段方法),要么完全忽略了上下文长度这一关键变量,只能预测一个平均性能水平。
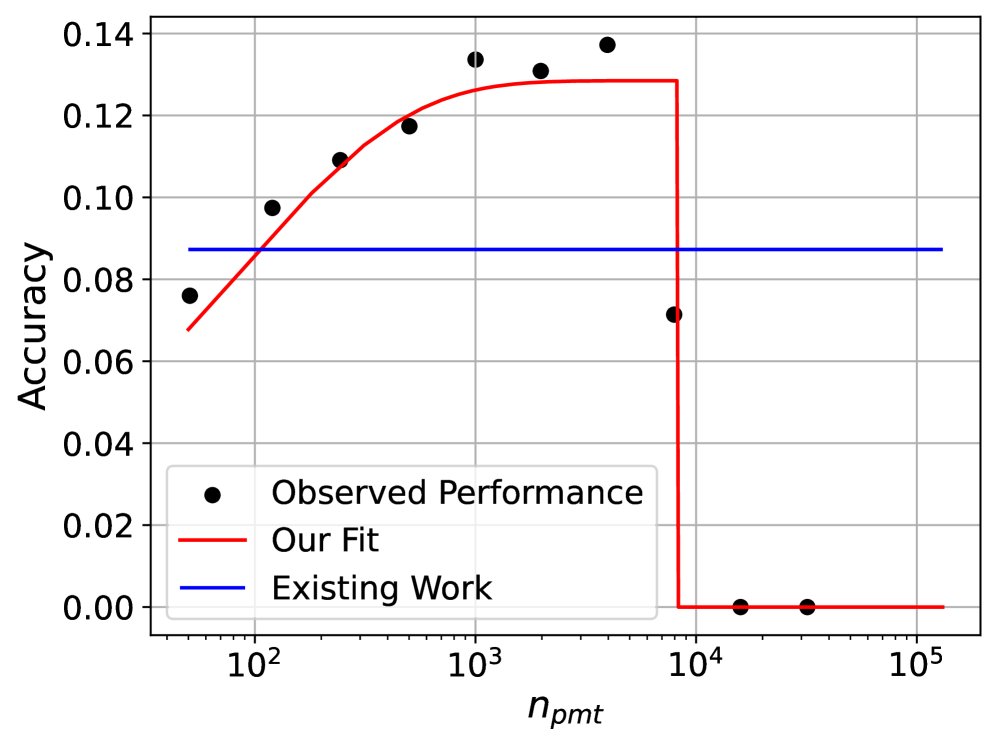
本文旨在解决这一问题,即创建一个简单、直接且可解释的框架,能够联合考虑训练计算量和上下文长度,从而更精确地预测 LLM 在不同上下文条件下的下游任务表现。
本文方法
本文提出一个函数框架,将下游任务的总体性能 $\mathcal{P}$ 建模为训练计算量 $C$ 和上下文长度 $n_{\text{pmt}}$ 的函数,并考虑了模型的上下文限制 $n_{\text{ctx}}$。
## 方法核心
该方法的核心是一个乘积形式的函数,包含三个关键部分:
- 计算量饱和项: 一个关于训练计算量 $C$ 的饱和幂律项。这部分基于一个直觉:随着计算量的增加,模型性能会提升,但这种提升效应会逐渐减弱并趋于饱和。
- 上下文饱和项: 一个关于上下文长度 $n_{\text{pmt}}$ 的饱和幂律项。这部分假设,在上下文内容相关的前提下,增加上下文长度能提升性能,但同样存在收益递减的饱和效应。
- 惩罚项: 一个 Sigmoid 函数形式的惩罚项。当输入上下文长度 $n_{\text{pmt}}$ 超过模型的上下文限制 $n_{\text{ctx}}$ 时,该项会急剧降低预测性能,以模拟模型在超长序列上推理能力骤降的现象。
公式的乘法结构体现了计算量和上下文的互补关系:任何一方的严重不足都会限制另一方带来的收益。例如,一个能力较弱(计算量低)的模型无法有效利用长上下文,反之亦然。
## 模型和数据
为了验证框架的有效性,本文基于 Llama-2-7B 和 Llama-2-13B 模型进行实验。由于原始 Llama-2 的上下文窗口较短(4k),本文使用 YaRN 方法对这些模型进行微调,将其上下文限制扩展到了 8k, 16k, 32k, 64k, 128k 等多个版本。
| 基础模型 | 非嵌入参数 ($N$) | 上下文限制 ($n_{\text{ctx}}$) | 数据集大小 ($D$) | 训练计算量 ($C$) |
|---|---|---|---|---|
| Llama-2-7B | 6,476,271,616 | 4k | 2.0T | $7.7719\times 10^{22}$ |
| 8k | 2.0T $+$ 0.210B | $7.7723\times 10^{22}$ | ||
| 16k | 2.0T $+$ 0.419B | $7.7732\times 10^{22}$ | ||
| 32k | 2.0T $+$ 0.836B | $7.7748\times 10^{22}$ | ||
| 64k | 2.0T $+$ 1.678B | $7.7780\times 10^{22}$ | ||
| 128k | 2.0T $+$ 3.355B | $7.7846\times 10^{22}$ | ||
| Llama-2-13B | 12,688,184,320 | 4k | 2.0T | $1.5227\times 10^{23}$ |
| 8k | 2.0T $+$ 0.210B | $1.5227\times 10^{23}$ | ||
| 16k | 2.0T $+$ 0.419B | $1.5229\times 10^{23}$ | ||
| 32k | 2.0T $+$ 0.836B | $1.5232\times 10^{23}$ | ||
| 64k | 2.0T $+$ 1.678B | $1.5239\times 10^{23}$ | ||
| 128k | 2.0T $+$ 3.355B | $1.5251\times 10^{23}$ |
实验在三个覆盖 65,500 个不同实例的下游任务上进行:
- 算术推理: 基于 GSM8K, MATH 等数据集。
- 常识推理: 基于 PIQA, HellaSwag 等数据集。
- 机器翻译: 基于 WMT-14 数据集。
## 拟合过程
对于每个任务,本文收集了不同模型、不同上下文长度下的性能数据点,然后使用一个两阶段优化程序(全局差分进化 + 局部优化)来拟合前述公式中的参数。
实验结论
实验结果表明,本文提出的框架能够高度准确地拟合下游任务的实际性能。
## 拟合精度
- 在算术推理、常识推理和机器翻译任务上,模型的平均绝对预测误差($ \mid \mathcal{P}-\hat{\mathcal{P}} \mid $)分别仅为 0.010、0.037 和 0.007,表现出极高的拟合精度。
- 该框架也很好地模拟了当上下文长度接近并超过模型限制时性能的变化趋势。
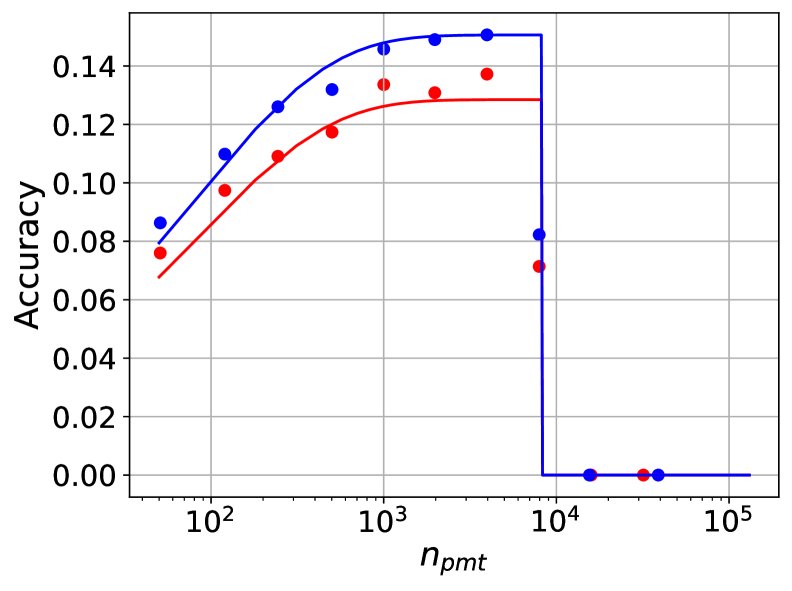
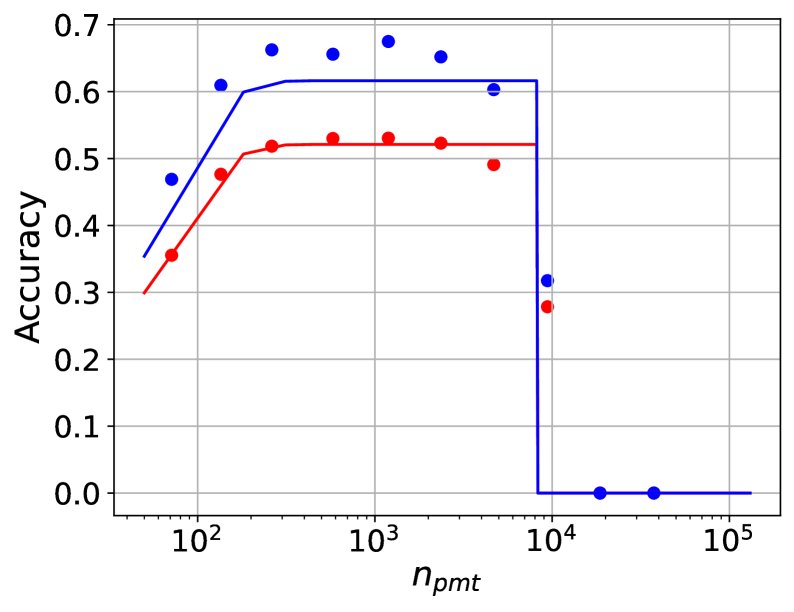
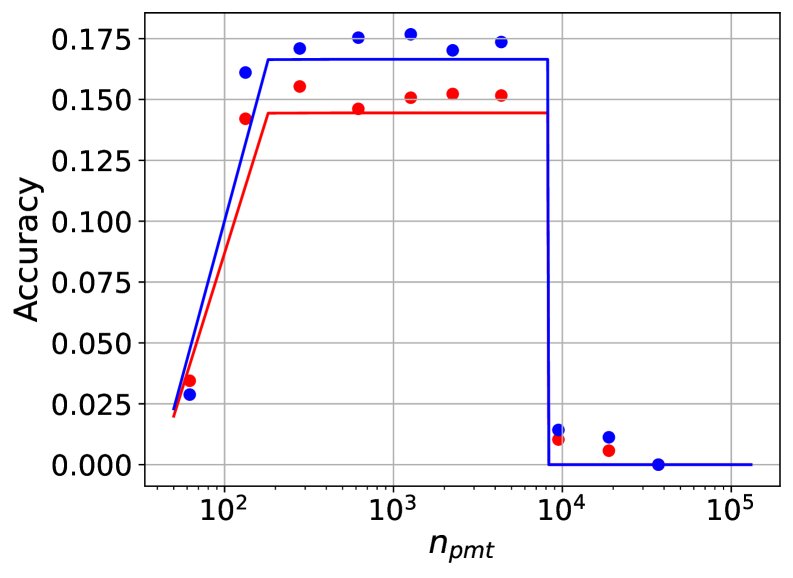
在 $n\_{\text{ctx}}=8k$ 时,Llama-2-7B (C≈7.8e22) 和 Llama-2-13B (C≈1.5e23) 在三个任务上的性能拟合等高线图。
## 泛化能力
本文进一步验证了拟合出的缩放定律在分布外(out-of-distribution)场景的泛化能力。
- 对更大计算量的泛化: 拟合曲线在未见过的模型(如 Qwen-2.5-0.5B, Gemma-2 系列, Llama-2-70B)上表现出良好的泛化能力,这些模型的计算量跨越了3个数量级。
- 对更长上下文的泛化: 在仅使用短上下文数据(<10k tokens)进行拟合后,该框架能可靠地外推预测模型在更长上下文(高达 128k)下的性能。在算术推理、常识推理和机器翻译的留出(held-out)数据上,预测误差分别仅为 0.017、0.067 和 0.006。
- 对不同上下文扩展技术的泛化: 实验比较了使用 YaRN 和位置插值(Positional Interpolation)两种不同技术扩展的 Llama-2-7B 模型,发现它们的性能变化同样符合本文提出的缩放定律,表明该定律对具体的上下文扩展技术不敏感。

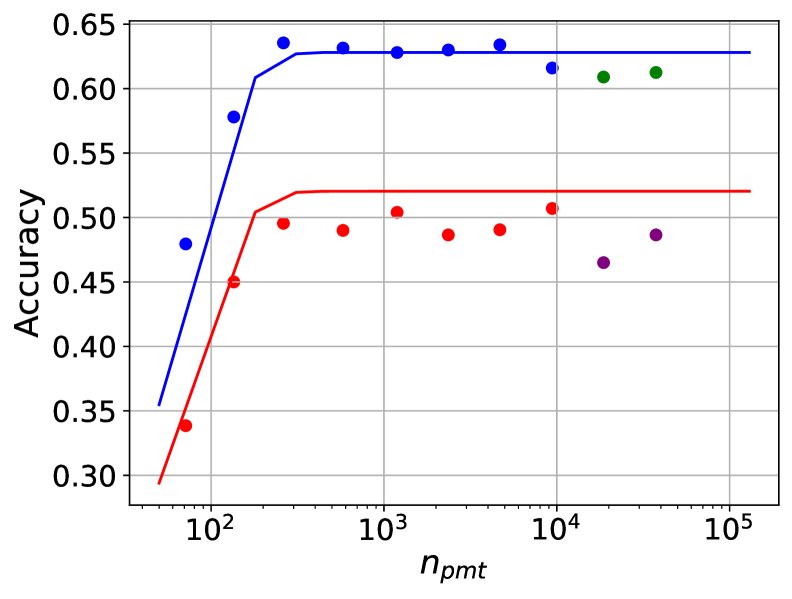
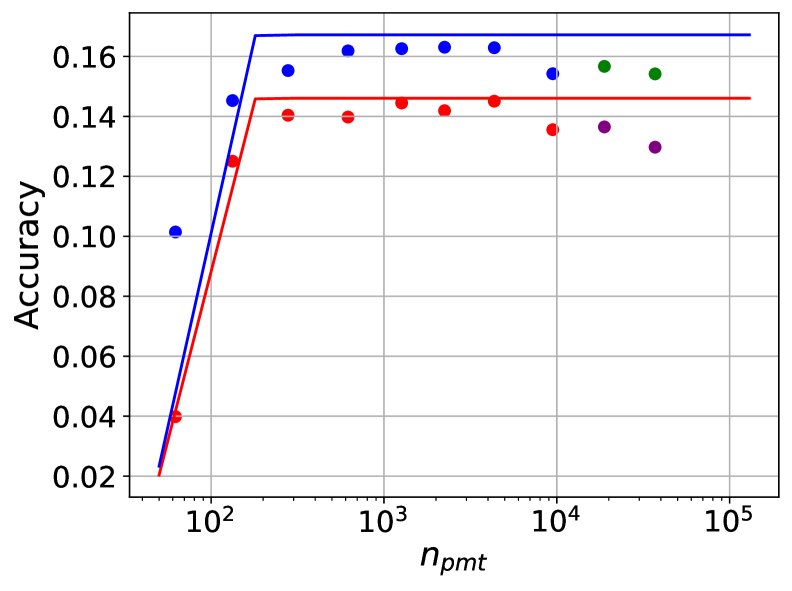
在 $n\_{\text{ctx}}=128\text{k}$ 时,对长上下文的泛化预测。图中实心点为未用于拟合的留出观测数据。
## 消融研究
通过移除惩罚项进行消融实验,结果显示,若没有惩罚项,模型在 $n_{\text{pmt}} \le n_{\text{ctx}}$ 时会低估性能,而在 $n_{\text{pmt}} > n_{\text{ctx}}$ 时会严重高估性能,这证实了惩罚项在准确建模中不可或缺。
| $ \mid P-\hat{P} \mid _{n_{\text{pmt}}\le n_{\text{ctx}}}$ | $ \mid P-\hat{P} \mid _{n_{\text{pmt}}>n_{\text{ctx}}}$ | $ \mid P-\hat{P} \mid $ | |
|---|---|---|---|
| 带惩罚项 | 0.010 | 0.014 | 0.010 |
| 不带惩罚项 | 0.019 | 0.104 | 0.029 |
算术推理任务上惩罚项的消融研究预测误差对比
## 总结
本文提出的上下文感知缩放定律框架,通过一个简单、可解释的函数形式,成功地将训练计算量和上下文长度这两个关键因素统一起来,实现了对 LLM 下游任务性能的精确预测。实验证明,该框架不仅拟合精度高,而且在模型计算量、上下文长度和上下文扩展技术上都具备出色的泛化能力,为设计和优化未来更高效的长上下文 LLM 提供了宝贵的洞见和实用的工具。